1961年~2023年まで、63年分の九大数学を研究しました。
その一部を公開します。
「学力を上げて九大を目指す」と考えると、九大合格できるのは
- 学区1位高校の
- 上位50%の学生さん
だけですが、そこに「合格を簡略化する」という発想を加えると
- 高校偏差値60の高校の
- ビリの学生さん
が九大合格できる所まで、難易度を下げられます。
| 高校 偏差値 | 6学区 | 5学区 | 4学区 | 3学区 | 2学区 |
|---|---|---|---|---|---|
| 63 | 香住丘 | ||||
| 62 | |||||
| 61 | 福岡中央 | 宗像 | |||
| 60 | 筑紫 | 新宮 | 八幡 | 戸畑 | |
| 59 | |||||
| 58 | |||||
| 57 | 筑前 | 筑紫中央 | 香椎 | 北筑 | 小倉西 |


本ページでは
- 1番簡単な国立大学を目指せない
- 九州工業大学・熊本大学など想像もできない
という学生さんが九大合格できている
- 九大数学のアプローチの仕方
- 簡単な合格点の作り方
を公開します。
- 九州大学の数学
- 弱者の勉強法「九大数学の攻略法」
- 九州大学の数学2023年・令和5年度
- 九州大学の数学2022年・令和4年度
- 九州大学の数学2021年・令和3年度
- 九州大学の数学2020年・令和2年度
- 九州大学の数学2019年・平成31年度
- 九州大学の数学2018年・平成30年度
- 九州大学の数学2017年・平成29年度
- 九州大学の数学2016年・平成28年度
- 九州大学の数学2015年・平成27年度
- 九州大学の数学2014年・平成26年度
- 九州大学の数学2013年・平成25年度
- 九州大学の数学2012年・平成24年度
- 九州大学の数学2011年・平成23年度
- 九州大学の数学2010年・平成22年度
- 九州大学の数学2009年・平成21年度
- 九州大学の数学2008年・平成20年度
- 九州大学の数学2007年・平成19年度
- 九州大学の数学2006年・平成18年度
- 九州大学の数学2005年・平成17年度
- 九州大学の数学2004年・平成16年度
- 九州大学の数学2003年・平成15年度
- 九州大学の数学2002年・平成14年度
- おわりに
九州大学の数学
基本データ
| 大問数 | 5問 |
| 試験時間 | 150分 |
| 配点 | 250点 |
- 大問数5問
| 2021年 | 2023年 | 2004年 | 2020年 | 2003年以前 | |
|---|---|---|---|
| 出題形式 | 必答 大問1~5 | 必答 大問1~5 | 必答 大問1~3 選択 大問4~6 大問7~9 |
| メイン 難易度 | 標準 | やや簡単~標準 | 標準~やや難しい |
- 配点
| 大問1つ | 50点 |
| 合計 | 250点 |
かなり簡単な大問でも、医学の合否を分ける難問でも、等しく50点です。
このため「難問を避け、簡単な問題で合格点を作る」作戦が有効です。
- 目標ライン
| 医学科 | 臨床薬科 | それ以外の 学部・学科 |
| 80% | 75% | 60% |
受験用データ
- 合格者最低点

- 難易度の変遷
| 年度 | 内容 | 目標得点率 |
|---|---|---|
| ~2003 | 難問・超難問が多い | 60% |
| 2002年 | ゆとり教育スタート | |
| 2004~2020 | 才能が無くても 努力すれば必ず正解できる | 56% |
| 2020年 | センター試験・終了 | |
| 2021~2023 | 3年連続で難化 | 50%台前半 |
2003年以前は難問がよく見られました。
2004年以降は「才能が無くても努力すれば必ず解ける問題」がメインとなり、大人しい試験が続きました。
その後、2021年(共通テスト開始)から3年連続で「難化」が続きました。
特に2022年は「過去30年で最難」と一騒ぎありましたが、「大問1・大問5が簡単」という抜け道があったため、2003年以前より簡単でした。
攻略用データ
以下の画像は九大数学の「出題分野」と「大問番号」です。

続いて、九大数学の「難易度」に関して。
以下の5段階で評価します。
| 難易度 | 評価 | 内容 |
|---|---|---|
| 1 | 簡単 | 共通テストと同等 |
| 2 | やや簡単 | 才能が無い人でも、訓練すれば必ず正解できるレベル |
| 3 | 普通 | 標準レベル |
| 4 | やや難しい | 「下位合格者さん」は完答できないレベル |
| 5 | 難問 | 医学科の合否を分ける問題 |
以下の表は、九大数学の「出題分野」と「難易度」です。
| 大問1 | 大問2 | 大問3 | 大問4 | 大問5 | 合計 | |
|---|---|---|---|---|---|---|
| 2023 | 2 | 3 | 4 | 5 | 2 | 16 |
| 高次方程式 | 数列 | ベクトル | 微分 | 微分積分 | ||
| 複素数 | 極限 | 整数 | ||||
| 2022 | 2 | 4 | 4 | 5 | 2 | 17 |
| ベクトル | 正式の除法 | 整数 | 微分積分 | 微分積分 | ||
| 極限 | 複素数 | |||||
| 2021 | 3 | 2 | 3 | 4 | 4 | 16 |
| 空間ベクトル | 複素数 | 微分積分 | 複素数 | 整数 | ||
| 2020 | 2 | 4 | 4 | 3 | 3 | 16 |
| 微分 | 複素数 | ベクトル | 確率 | 積分 | ||
| 整数 | ||||||
| 2019 | 1 | 3 | 3 | 3 | 4 | 14 |
| 積分 | 整式 | 2次方程式 | 数列 | 複素数 | ||
| 極限 | 確率 | 極限 | ||||
| 複素数 | ||||||
| 2018 | 2 | 2 | 3 | 4 | 4 | 15 |
| 2次曲線 | 図形と方程式 | 確率 | 整数 | 複素数 | ||
| 軌跡 | 積分 | 数列 | 3次方程式 | |||
| 2017 | 2 | 1 | 4 | 2 | 4 | 13 |
| 微分積分 | ベクトル | 数列 | 確率 | 複素数 | ||
| 整数 | 数列 | |||||
| 2016 | 2 | 2 | 1 | 3 | 2 | 10 |
| 微分積分 | ベクトル | 確率 | 整数 | 三角関数 | ||
| 極限 | 複素数 | |||||
| 2015 | 2 | 3 | 3 | 2 | 4 | 14 |
| 積分 | 微分積分 | 積分 | 確率 | 整数 | ||
| 2014 | 1 | 3 | 3 | 1 | 5 | 13 |
| 微分積分 | 論理と集合 | 図形と方程式 | 場合の数・確率 | 微分 | ||
| 2次曲線 | ||||||
| 2013 | 2 | 2 | 2 | 3 | 4 | 13 |
| 極限 | 空間ベクトル | 場合の数・確率 | 積分 | 行列 | ||
| 微分 | ||||||
| 2012 | 2 | 3 | 4 | 4 | 2 | 15 |
| 積分 | 行列 | 2次関数 | 極限 | 場合の数・確率 | ||
| 極限 | ||||||
| 2011 | 1 | 2 | 3 | 3 | 2 | 11 |
| 積分 | 微分 | 数列 | 空間ベクトル | 場合の数・確率 | ||
| 2010 | 2 | 2 | 3 | 3 | 5 | 15 |
| 三角比 | 場合の数・確率 | 極限 | 積分 | 行列 | ||
| 微分 | 2次曲線 | |||||
| 2009 | 1 | 4 | 3 | 5 | 3 | 16 |
| 平面ベクトル | 確率 | 微分積分 | 行列 | 微分 | ||
| 2008 | 2 | 2 | 2 | 2 | 4 | 12 |
| 関数 | 確率 | 平面ベクトル | 微分積分 | 三角関数 | ||
| 極限 | ||||||
| 2007 | 1 | 3 | 3 | 1 | 5 | 13 |
| 微分積分 | 行列 | 空間ベクトル | 場合の数・確率 | 三角関数 | ||
| 2006 | 3 | 1 | 4 | 2 | 5 | 15 |
| 極限 | 平面ベクトル | 数列 | 三角関数 | 関数 | ||
| 微分 | 積分 | |||||
| 2005 | 1 | 3 | 2 | 5 | 3 | 14 |
| 微分積分 | 行列 | 複素数 | 三角関数 | 微分積分 | ||
| 指数対数 | ||||||
| 2004 | 3 | 2 | 2 | 3 | 3 | 13 |
| 極限 | 行列 | 微分積分 | 空間ベクトル | 場合の数・確率 | ||
| 積分 | 確率分布 |
| 難易度 | 内容 | 問題数 |
|---|---|---|
| 1 | 簡単 | 11問 |
| 2 | やや簡単 | 32問 |
| 3 | 普通 | 30問 |
| 4 | やや難しい | 19問 |
| 5 | 難問 | 8問 |
| 計 | 100問 |
平均難易度:2.81(2004~2023年)
難易度1~3だけで73/100問ある事に注目してください。
難しい問題は避け、簡単な問題を狙い、合格点を作ります。
| 右記以外 | 医学科 臨床薬科 | |
|---|---|---|
| 合格形 | 2完答 + 3部分点 | 3完答 + 2部分点 |
| 目標得点率 | 56% | 80% |
では、九州大学の攻略法スタートです。
攻略法1「1番簡単な大問」から。
弱者の勉強法「九大数学の攻略法」
1番簡単な大問を正解する
「5問中2完答」で九大合格できます。
全5問の内、「1番簡単な大問」は突出して簡単です。
高校偏差値50(国立大学の進学者ほぼ0名)の高校以上なら、訓練すれば必ず正解できるようになります。
まず、この1問を正解してください。
20年間(2004~2023)の出題分野は以下の通りです。
| 1番簡単な 大問番号 | 分野 | 難易度 | |
|---|---|---|---|
| 2023 | 1 | 複素数 | 2 |
| 2022 | 1 | ベクトル | 2 |
| 2021 | 2 | 複素数 | 2 |
| 2020 | 1 | 微分 | 2 |
| 2019 | 1 | 積分・極限 | 1 |
| 2018 | 2 | 図形・積分 | 2 |
| 2017 | 2 | ベクトル | 1 |
| 2016 | 1 | 微積・極限 | 2 |
| 2015 | 1 | 積分 | 2 |
| 2014 | 1 | 微積 | 1 |
| 2013 | 2 | 微分・極限 | 2 |
| 2012 | 1 | 積分 | 2 |
| 2011 | 1 | 積分 | 1 |
| 2010 | 2 | 場合の数・確率 | 2 |
| 2009 | 1 | ベクトル | 1 |
| 2008 | 1 | 微分・極限 | 2 |
| 2007 | 1 | 微積 | 1 |
| 2006 | 2 | ベクトル | 1 |
| 2005 | 1 | 微積 | 1 |
| 2004 | 3 | 微積 | 2 |
| 分野 | 問題数 |
|---|---|
| 微分・積分 | 13問 65.0% |
| ベクトル | 4問 20.0% |
| 複素数 | 2問 10.0% |
| 場合の数・確率 | 1問 5.0% |
| 合計 | 20問 2004~2023 |
1番簡単な問題は「微分積分」が多いです。
また、微分積分は
- 2番目に簡単な問題
- 3番目に簡単な問題
になる場合も多く、微積だけで2完答できる年もあります。
| カッコ内は 難易度 | 微積で 2完答 | 微積で 得点率60% |
|---|---|---|
大問5(2) | ||
大問5(2) | ||
| 2020 | 大問1(難易度2) 大問5(3) | |
| 2015 | 大問1(2) 大問2(3) 大問3(3) | |
| 2013 | 大問1(2) 大問4(3) | |
| 大問1(1) | ||
| 2011 | 大問1(1) 大問2(2) | |
| 2010 | 大問3(3) 大問4(3) | |
| 2009 | 大問3(3) 大問5(3) | |
| 2006 | 大問1(3) 大問4(2) | |
| 2005 | 大問1(1) 大問5(3) | |
| 2004 | 大問1(3) 大問3(2) | |
| 2001 | 大問1 大問3 大問5(選択) |
よって、まず「微分積分」を集中的に勉強してください。
高確率で1問完答できます。
これで、残り4問から「1完答+3部分点」で九大合格です。
次は、攻略法2「1番難しい大問」です。
1番難しい問題を回避する
全5問の内、「1番難しい大問」は突出して難しいです。
見分けて回避してください。
| 難易度 | 回避の方法 |
|---|---|
| 4 やや難しい | 小問1だけ正解し「大問丸ごと0点」を防げば良いです。後は、行ける所までで十分です。 |
| 5 難問 | 小問1から解けなくても仕方ないです。時間の浪費を防いでください。 |
難易度1~3を勉強すれば、難易度4~5は「明らかに難しい」と、すぐ見えるようになります。
よって「難問を見分ける方法」は必要ありません。
これで、残り3問から「1完答+2部分点」で九大合格となります。
最後に、攻略法3「2つ目の完答」です。
2つ目の完答の狙い方
残った問題は
- 2番目に簡単な問題
- 3番目に簡単な問題
- 4番目に簡単な問題
の3つです。
年度により「難易度」に差があるので、データを確認しましょう。
| 2番目に 簡単な大問 | 3番目に 簡単な大問 | 4番目に 簡単な大問 | 年度 |
|---|---|---|---|
| やや簡単 | やや簡単 | やや簡単 | 16,08 |
| やや簡単 | やや簡単 | やや普通 | 13,11 |
| やや簡単 | やや簡単 | やや難しい | 17 |
| やや簡単 | 普通 | 普通 | 15,14,07,05,04 |
| やや簡単 | 普通 | やや難しい | 23,20,18,12,10,06 |
| やや簡単 | やや難しい | やや難しい | 22 |
| 普通 | 普通 | 普通 | 19 |
| 普通 | 普通 | やや難しい | 21,09 |
上記より
- 2番目は「やや簡単」が来やすい
- 3番目は「普通」が来やすい
- 4番目は「やや難しい」と「普通」が半々
と解ります。
| 才能の無い学生さんにとって | |
|---|---|
| やや簡単 | 訓練すれば 必ず解けるようになる |
| 普通 | 難しい分野でなければ 必ず解けるようになる |
よって、才能がない学生さんでも
- 2番目に簡単な大問
- 3番目に簡単な大問
からは、2完答目を取れます。
狙い目の分野は、以下のデータから解ります。
| 微分積分 | 大問番号 | 難易度 |
|---|---|---|
| 2023 | 4 | 5 |
| 5 | 2 | |
| 2022 | 4 | 5 |
| 5 | 2 | |
| 2021 | 3 | 3 |
| 2020 | 1 | 2 |
| 5 | 3 | |
| 2019 | 1 | 1 |
| 2018 | 2 | 2 |
| 2017 | 1 | 2 |
| 2016 | 1 | 2 |
| 2015 | 1 | 2 |
| 2 | 3 | |
| 3 | 3 | |
| 2014 | 1 | 1 |
| 5 | 5 | |
| 2013 | 1 | 2 |
| 4 | 3 | |
| 2012 | 1 | 2 |
| 2011 | 1 | 1 |
| 2 | 2 | |
| 2010 | 3 | 3 |
| 4 | 3 | |
| 2009 | 3 | 3 |
| 5 | 3 | |
| 2008 | 4 | 2 |
| 2007 | 1 | 1 |
| 2006 | 1 | 3 |
| 4 | 2 | |
| 2005 | 1 | 1 |
| 5 | 3 | |
| 2004 | 1 | 3 |
| 3 | 2 | |
| 平均難易度 | 2.48 | |
| 出題数 | 33/100問 |
| ベクトル | 大問番号 | 難易度 |
|---|---|---|
| 2023 | 3 | 4 |
| 2022 | 1 | 2 |
| 2021 | 1 | 3 |
| 2020 | 3 | 4 |
| 2017 | 2 | 1 |
| 2016 | 2 | 2 |
| 2013 | 2 | 2 |
| 2011 | 4 | 3 |
| 2009 | 1 | 1 |
| 2008 | 3 | 2 |
| 2007 | 3 | 3 |
| 2006 | 2 | 1 |
| 2004 | 4 | 3 |
| 平均難易度 | 2.38 | |
| 出題数 | 13/100問 |
| 複素数平面 | 大問番号 | 難易度 |
|---|---|---|
| 2023 | 1 | 2 |
| 2022 | 5 | 2 |
| 2021 | 2 | 2 |
| 4 | 4 | |
| 2020 | 2 | 4 |
| 2019 | 3 | 3 |
| 5 | 4 | |
| 2018 | 5 | 4 |
| 2017 | 5 | 4 |
| 2016 | 5 | 2 |
| 2005 | 3 | 2 |
| 平均難易度 | 3.00 | |
| 出題数 | 11/50問 (2016年に復活) |
| 場合の数・確率 | 大問番号 | 難易度 |
|---|---|---|
| 2020 | 4 | 3 |
| 2019 | 3 | 3 |
| 2018 | 3 | 3 |
| 2017 | 4 | 2 |
| 2016 | 3 | 1 |
| 2015 | 4 | 2 |
| 2014 | 4 | 1 |
| 2013 | 3 | 2 |
| 2012 | 5 | 2 |
| 2011 | 5 | 2 |
| 2010 | 2 | 2 |
| 2009 | 2 | 4 |
| 2008 | 2 | 2 |
| 2007 | 4 | 1 |
| 2004 | 5 | 3 |
| 平均難易度 | 2.20 | |
| 出題数 | 15/100問 |
| 整数 | 大問番号 | 難易度 |
|---|---|---|
| 2023 | 3 | 4 |
| 2022 | 3 | 4 |
| 2021 | 5 | 4 |
| 2020 | 2 | 4 |
| 2018 | 4 | 4 |
| 2017 | 3 | 4 |
| 2016 | 4 | 3 |
| 2015 | 5 | 4 |
| 平均難易度 | 3.88 | |
| 出題数 | 8/100問 |
| 極限 | 大問番号 | 難易度 |
|---|---|---|
| 2023 | 2 | 3 |
| 2022 | 2 | 4 |
| 2019 | 1 | 1 |
| 4 | 3 | |
| 2016 | 1 | 2 |
| 2013 | 1 | 2 |
| 2012 | 3 | 4 |
| 4 | 4 | |
| 2010 | 3 | 3 |
| 2008 | 1 | 2 |
| 2006 | 1 | 3 |
| 2004 | 1 | 3 |
| 平均難易度 | 2.83 | |
| 出題数 | 12/100問 |
| 数列 | 大問番号 | 難易度 |
|---|---|---|
| 2023 | 2 | 3 |
| 2019 | 4 | 3 |
| 2018 | 3 | 3 |
| 2017 | 3 | 4 |
| 4 | 2 | |
| 2011 | 3 | 3 |
| 2006 | 3 | 4 |
| 平均難易度 | 3.14 | |
| 出題数 | 7/100問 |
| 三角関数 | 大問番号 | 難易度 |
|---|---|---|
| 2016 | 5 | 2 |
| 2008 | 5 | 4 |
| 2007 | 5 | 5 |
| 2006 | 4 | 2 |
| 2005 | 4 | 5 |
| 平均難易度 | 3.60 | |
| 出題数 | 5/100問 |
以上のデータより
- 絶対に欠かせない分野
- 狙い目の分野
- 努力が報われにくい分野
に分けたものが以下の表です。
| 分野 | 平均難易度 | 出題率 |
|---|---|---|
| 微分積分 | 2.48 | 33% |
| 場合の数・確率 | 2.20 | 15% |
| ベクトル | 2.38 | 13% |
| 極限 | 2.83 | 12% |
| 複素数 | 3.00 | 22% |
| 数列 | 3.14 | 7% |
| 三角関数 | 3.60 | 5% |
| 整数 | 3.88 | 8% |
以上のデータに
- 分野の重要度
- 他分野とのシナジー
- 学びやすさ
を加えると「重視すべき順番」は以下のようになります。
| 分野 | 理由 | |
|---|---|---|
| 1位 | 微分積分 | 攻略法1 過去の出題確率100% 2出題も多い |
| 2位 | ベクトル | 学びやすい 簡単な問題が多い 微分積分とのシナジー |
| 3位 | 極限 | 微分積分とのシナジー |
| 4位 | 場合の数・確率 | 2007~2020まで 14年連続出題 簡単な問題が多い |
| 5位 | 複素数 | 2016~2023まで 8年連続出題 2021~2023まで 3年連続で難易度2 |
| 6位 | 整数 | 2020~2023まで 4年連続で出題 難しい分野 |
| 7位 | 数列 | ここまで得意にできれば 懐が深くなって心強い |
この順に得意にしておけば、才能が無い学生さんでも、高確率で「2完答」できるようになります。
以上で、攻略法3「2つ目の完答の狙い方」は終わりです。
九大数学の攻略法4以降
- 分野ごとの「正解すべき問題」と「捨てるべき問題」
- 「センター試験時代」と「共通テスト開始後」の傾向の変化
- 才能別(トップ高校、2番手高校、中卒・中退・ひきこもり等)の勉強法
- 英語・物理・化学の攻略法との併用
- 5教科トータル「九州大学の攻略法」
など、細かく別れていきます。
| 攻略法1~3 | 幹・太い枝 | 最小限の動きで 得点率56%の状態を作る (まず合格を確保する) |
| 攻略法4以降 | 枝・葉 | 基礎を重視し 簡単な順に 1%ずつ上げていく |
| 攻略法・終章 | 根 | 5教科トータルの 合格作戦に昇華 |
九州大学の数学2023年・令和5年度
大問1

講師としての解説
「高次方程式」と「複素数平面」からの出題です。
計算量・難易度に関して、やや簡単です。問1・問2ともに計算テクニックが必要ですが、定番の方法です。閃きの必要性に関して、やや簡単です。(2)の式変形の過程で「(1)と同じ」と気付けるかがポイントです。知識の要性に関して、少し必要です。小問2で「文字が循環」している方程式の定石を使います。
問1に関して、計算問題です。4次方程式の解を求めます。
ポイントは「x²で割ること」です。
式全体をカッコでくくれるようになります。割算なので「x≠0」の確認に注意してください。
- x⁴-2x³+3x²-2x+1=0・・・①
- ①においてx=0は成り立たない
- x≠0より
①をx²でわると
x²-2x+3-2/x+1/x²=0
∴ (x+1/x)²-2(x+1/x)+1=0
∴(x+1/x-1)²=0
∴ x+1/x-1=0
∴ x²-x+1=0 - 解の公式より
\(x=\dfrac{1\pm \sqrt{3}i}{2}\)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、与式が表す「三角形の形」を答えます。
ポイントは、α・β・γが「均等な関係」になっていることです。
1ヶ所を固定し、基準を作ると上手く行きます。
- (α-β)⁴+(β-γ)⁴+(γ-α)⁴=0・・・②
∴(β-α)⁴+{(β-α)-(γ-α)}⁴+(γ-α)⁴=0 - 題意より、β-α≠0なので
辺々(β-α)⁴で割ると
\(1+\left( 1-\dfrac{r-\alpha }{\beta -\alpha }\right) ^{4}+\left( \dfrac{\gamma -\alpha }{\beta-\alpha }\right) ^{4}=0\)
となる - 今、\(\dfrac{\gamma -\alpha }{\beta-\alpha }=X\)とおくと
1+(1-X)⁴+X⁴=0
∴ X⁴-2X³+3X²-2X+1=0 - (1)の結果より
\(X=\dfrac{1\pm \sqrt{3}i}{2}\) - ゆえに
\(\begin{aligned}\dfrac{\gamma -\alpha }{\beta -\alpha }=\cos \left( \pm \dfrac{\pi }{3}\right) +i\sin \left( \pm \dfrac{\pi }{3}\right) \ \end{aligned}\)(複号同順) - よって
|(γ-α)/(β-α)|=1より
AB=ACであり
arg(γ-α)/(β-α)=±π/3より
∠BAC=π/3なので
三角形ABCは「正三角形」
(これが正解です)
- (β-α)による1ヶ所の固定
- 問1の活用
- 図形への落とし込み
と3つハードルがありますが、1つ1つは難しくありません。
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
受験生としての解説
2023年の九大数学5問中、1番簡単な問題です。
九大数学は5つの大問から「2完答+3部分点」で非医歯薬系の合格得点率56%を作れます。近年の九大数学は「難しい、難しい」とよく言われますが、合格点を取るだけなら大問1・大問5のレベルで可能です。
- 計算:★★(やや簡単)
- 閃き:★★(やや簡単)
- 知識:★★(やや簡単、定番の計算テクニック)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問2

講師としての解説
「数列」からの出題です。
計算量・難易度に関して、普通程度です。計算は最後までシンプルなままです。閃きの必要性に関して、普通程度に必要です。自分で数値を代入し、法則性を見つけ、自分で解答方針を決めます。知識の必要性に関して、やや少なめです。数列・極限の知識が必要です。
問1に関して、α≦1における「数列{an}の収束・発散」を調べます。
ポイントは「帰納的に考えること」です。
与式に「n=1」から代入していくと「n=2」以降は0ばかり出力されます。よって、帰納的に0とわかるので、数学的帰納法を使います。
- 与式より
a₂=|a₁-1|+a₁-1=0・・・① - ある自然数mで
am=0
が成り立つと仮定する - この時
am+1=|am-1|+am-1=0・・・② - ゆえに①②より
an=0(n≧2)
となる - よって
liman=0に収束する
(これが正解です)
「数学的帰納法」に持ち込めるかが、合否の分かれ目です。
ここを乗り越えれば、小問3まで同じ方法で正解できます。
よって、本問が「小問3つ分の運命を背負っている」という意味で、合否を分ける1問です。
問2に関して、α>2における「数列{an}の収束・発散」を調べます。
ポイントは「帰納的に考えること」です。
与式に「n=1」から代入していくと「2より大きな値」ばかり出力されます。よって、帰納的に「2より大きい」とわかるので、数学的帰納法を使います。
- a₂=2a₁-2
=2(a₁-1)
>2(2-1)=2・・・① - 今、ある自然数mに対して
am>2
が成り立つと仮定する - この時
am₊₁=2(am-1)
>2(2-1)=2・・・②
となる - よって①②とa₁=α>2より
全ての自然数nに関して
an+1=2an-2
となる
∴ an₊₁-2=2(an-2)
∴ an-2=(a₁-2)2^n-1
∴ an=2+(α-2)2^n-1 - 今、α-2>0より
liman=∞に発散する
(これが正解です)
実質、問1と同じ問題です。
よって、問1とセットで、合否を分ける1問です。
問3に関して、1<α<3/2における「数列{an}の収束・発散」を調べます。
ポイントは「帰納的に考えること」です。
n=1から数値を代入していくと、n=3で0が出力されると判ります。よって、以降「ずっと0が続く」事は問1で証明済みなので、この時点で正解となります。
- 与式より
a₂=|α-1|+α-1
=2α-2 - 今、1<α<3/2より
0<2α-2<1
∴ 0<a₂<1 - この時
a₃=|a₂-1|+a₂-1
=0 - よって、問1の結果より
an=0(n≧3)
となるため
liman=0に収束する
(これが正解です)
実質、問1と同じ問題です。
よって、問1とセットで、合否を分ける1問です。
問4に関して、3/2≦α<2における「数列{an}の収束・発散」を調べます。
ポイントは「帰納的に考えること」です。
n=1から数値を代入しても、絶対値内で「場合分け」が発生するため、なかなか法則性が見えてきません。しかし「項の取りうる最小値」がどんどん小さくなっていく事は読み取れます。
- 3/2≦a₁<2
- 1≦a₂<2
- 0≦a₃<2
よって
- 数列が進むほど、項の値は小さくなる
- よって絶対値の中身は、数列が進むと負になる
- よって小問1と同じ形になり、数列の極限は「0に収束する」
と予測が立ちます。
よって「背理法」に持ち込みます。「0に収束しない」と仮定を立て、矛盾を示す流れです。
- 全ての自然数nでan>1が成り立つ…④
と仮定すると
an+1=|an-1|+an-1
=2an-2
∴an=(α-2)2^n-1+2…⑤
となる - 3/2≦α<2の時
α-2<0より式⑤は
liman=-∞
となり、④の仮定に矛盾する - よって、ある自然数nでan≦1となるため
小問1の結果より
数列{an}は0に収束する
(ここが正解です)
合格者さんでも難しい問題です。
よって、正解できれば他者に差をつける1問です。
受験生としての解説
2023年の九大数学5問で、3番めに簡単な問題です。
2023年は、大問4がかなり難しそうに見える(実際は難問ではない)ので、試験中に「大問4は部分点さえ稼ぎにくい」と感じるでしょう。そうなると
- 大問1・大問5を完答
- 大問2・大問3の部分点で勝負
という流れになります。よって、小問4を正解(大問2を完答)できると大きな追加点となります。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★(やや少なめ)
- 総合:★★★(普通)
- 短評:小問3まで正解したい
大問3

講師としての解説
「ベクトル」と「整数」からの出題です。
計算量・難易度に関して、やや難しいです。a,b,c,dはいずれも「0を取りうる」ので、分数や割算を扱う際は注意が必要です。閃きの必要性に関して、やや強く必要です。与えられた条件をその場で理解し、その場で応用するタイプの問題です。知識の必要性に関して、普通程度です。「ベクトル」と「整数」の基本知識が必要です。
問1に関して、条件Ⅰがすべての→qに対して成り立つ時「D≠0」を示します。
ポイントは「ベクトルの平行」です。
D≠0の時は、→mと→nが平行でないため「組み合わせ次第で」あらゆるベクトルを表現できます。しかし、D=0の時は「→mと→nが平行」になってしまうため、直線しか表せません。
これを利用し「D=0」から背理法に持ち込みます。
- D=0であると仮定すると
ab-bc=0
および
→m≠→0
より
→m//→nとなる - 今、ある実数k(≠0)を用いて
→m=k・→nと表すと
条件Ⅰの式は
(r+ks)→m=→qとなるが
→qが→mに平行なものしか表せないため
題意に反する - よって
条件Ⅰが全ての→qに対して成り立つ時
D≠0である(証明終了)
「背理法」を使うことは解りやすいですが、矛盾を表現する部分がやや難しいです。
不合格者さんの一定数が不正解になるレベルなので、合否を分ける1問より少し簡単な問題です。
問2に関して、以下の式を満たす「vベクトル,wベクトル」を答える問題です。
- →m・→v=→n・→w=1
- →m・→w=→n・→v=0
ポイントは
- →v=(x,y)
- →w=(X,Y)
と置いて計算することです。
計算は「内積=1、内積=0」の式を立てるだけです。
- →m・→v=1
→n・→v=0より
ax+cy=1・・・①
bx+dy=0・・・② - ①②をxyについて解くと
x=d/(ad-bc)=d/D
y=-b/(ad-bc)=-b/D - よって
→v=(d/D,-b/D)
(これが正解です) - 同様にして
→w=(-c/D,a/D)
(これが正解です)
「内積=1、内積=0」の式を立てるだけなので、不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、以下2つの条件において「Dの取りうる値」を答えます。
- a,b,c,dが全て整数
- →qのx成分・y成分が整数
ポイントは「問1・問2の応用」です。
問1の結果に問2を加えると「rとs」が求まります。ここに
- D=ad-bc
- D≠0
- a,b,c,dは全て整数
- →qのx成分・y成分は整数
という条件を加えると「D=±1」以外では成り立たない事が判ります。よって、D=±1が正解・・・という流れです。
- 整数x,yを用いて
→q=(x,y)
と表す - 与式r→m+s→n=→q
および問2の結果より
r→m・→v+s→n・→v=→q・→v
∴r・1+s・0
=(x,y)(d/D,-b/D)
∴ r=(dx-by)/D…③ - 同様にして
r→m・→w+s→n・→w=→q・→w
∴r・0+s・1=(x,y)(-c/D,a/D)
∴s=(ay-cx)/D…④ - ところで題意より
全ての整数x・yで与式が成り立つ条件を求めるので
(x,y)=(1,0)(0,1)
でも成り立つ必要がある - ③④に(x,y)=(1,0)を代入すると
この時のr,sをr₁,s₁として
r₁=d/D
s₁=-c/D
∴d=r₁D,c=-s₁D…⑤ - また③④に(x,y)=(0,1)を代入すると
この時のr,sをr₂,s₂として
r₂=-b/D
s₂=a/D
∴b=-r₂D,a=s₂D…⑥ - ⑤⑥をD=ad-bcに代入して
D=s₂D・r₁D-(-r₂D)(-s₁D)
∴1/D=s₂r₁-r₂s₁…⑦(∵D≠0) - ここで⑦の右辺は整数なので
左辺も整数でなければならない
よって求めるDの条件は
D=±1(これが正解です)
「整数」という条件の利用法が見えにくいため、合格者さんでも難しいレベルです。
医学科の合否を分ける1問です。
受験生としての解説
2023年の九大数学5問で、4番目に簡単な問題です。
合格点を取るだけなら
- 問1:→m // →nでは任意のベクトルが表現できないこと
- 問2:内積=1、内積=0の計算
で可能です。これらは問題集で練習できます。
- 計算:★★★★(やや多い)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:問2まで解きたい
大問4

講師としての解説
「微分」からの出題です。
計算量・難易度に関して、難しいです。論述と並行して抽象的な計算が続きます。難関大特有の難しい式変形があります。閃きの必要性に関して、強く必要です。試験中に長い問題文を読んで条件を理解し、応用するタイプの問題です。知識の必要性に関して、普通程度です。「微分可能の定義」が必要です。
問1に関して、証明問題です。条件(A)(B)(C)から「f(0)=1、g(0)=0」が成り立つことを示します。
ポイントは「x=0、y=0を代入すること」です。
- (A)(B)にx=0,y=0を代入すると
f(0)=f(0)²-g(0)²・・・(Ⅰ)
g(0)=2f(0)g(0)・・・(Ⅱ) - (Ⅱ)において、g(0)≠0とすると
f(0)=1/2 - (Ⅰ)に代入して
g(0)²=-1/4 - これはg(0)が実数であることに反するので
g(0)=0 - これを(Ⅰ)に代入すると
f(0)=1(証明終了)
g(x)にx=0を代入して矛盾を示すだけなので、不合格者さんでも一定数が正解してきます。
よって、合否を分ける1問より少し簡単な問題です。
問2に関して、証明問題です。f(x)がすべてのxの値で微分可能な関数であり、f'(x)=-g(x)となることを示します。
ポイントは「微分可能の定義」です。
【微分可能の定義】
関数f(x)がx=aで微分可能であるとは、x=aにおける微分係数
\(f’\left( a\right) =\lim _{h\rightarrow 0}\dfrac{f\left( a+h\right) -f\left( a\right) }{h}\)
が存在することである。
導関数の定義から、難関問題集でよく見かける式変形を経て正解となります。
- f(x+h)-f(x)/h
={f(x)f(h)-g(x)g(h)-f(x)}/h
=f(x)・{f(h)-1}/h – g(x)・{g(h)-0}/h
=f(x)・{f(h)-f(0)}/h – g(x)・{g(h)-g(0)}/h - よって
f'(x)=lim{f(x+h)-f(x)}/h
=f(x)f'(0)-g(x)g'(0)
=-g(x)(証明終了)
「微分可能の定義」は不合格者さんには厳しく、合格者さんは正解してきます。
よって、合否を分ける1問です。
問3に関して、証明問題です。{f(x)+ig(x)}(cosx-isinx)=1となる事を示します。
ポイントは「実部と虚部に分けて考えること」です。「微分係数=0」によって定数である事を示し、続いて「x=0」の代入によって実部・虚部の定数が各々1・0と証明でき、正解となります。問2が白紙解答になった人でも問3を正解できます。
- F(x)=f(x)cosx+g(x)sinx
G(x)=-f(x)sinx+g(x)cosx
とおく - F'(x)=f'(x)cosx-f(x)sinx+g'(x)sinx+g(x)cosx
=0(∵ 下線部②) - よってF(x)は定数であり
F(0)=f(0)cos0+g(0)sin0=1 より
F(x)=1 - 同様に
G'(x)=-f'(x)sinx-f(x)cosx+g'(x)cosx-g(x)sinx
=0 - よってG(x)は定数であり
G(0)=-f(0)sin0+g(0)cos0=0 より
G(x)=0(証明終了)
与式を「実部と虚部」に分解して「実部=1,虚部=0」を示すことは、不合格者さんでも一定数は気づけます。
よって、合否を分ける1問より少し簡単な問題です。
問4に関して、証明問題です。(B)の証明は、与式の右辺を展開・変形すると比較的容易に求まります。(D)の証明は導関数の定義から行います。難関問題集でよく見かける難しい式変形があり、(e^x-1/x)の極限公式を使うと正解できます。空欄ア・イは本問全体の結論となる問題です。
まずは(B)の証明から。
- p(x)q(y)+q(x)p(y)
=e^-ax/b・e^-ay/b{f(x/b)q(y/b)+g(x/b)f(y/b)}
=e^-a(x+y)/b・q(x/b+y/b)
=q(x+y) - よって(B)が成り立つことを示せた
(証明終了)
続いて(D)を証明します。
まず「p'(0)=0」の証明から。
- {p(h)-p(0)}/h
{e^-ah/b・f(h/b)-1}/h
=1/b・e^-ah/b・{f(h/b)-f(0)}/(h/b)+(e^-ah/b-1)/(-ah/b)・(-a/b)
赤い部分に以下の公式を使います。
x→0、lim(e^x-1)/x=1
- lim{p(h)-p(0)}/h(limはh→0)
=1/b・1・f'(0)+1・(-a/b)
=0 - よって
p'(0)=0
(証明終了)
続いて(D)の後半「q'(0)=1」の証明です。
- {q(h)-q(0)}/h
={e^-ah/b・q(h/b)}/h
=1/b・e^-ah/b・{g(h/b)-g(0)}/(h/b) - lim{g(h)-g(0)}/h(limはh→0)
=1/b・1・g'(0)
=1 - よって
g'(0)=1
(証明終了)
最後に「ア」「イ」を求めます。
- 条件(A)~(D)において
f(x)をp(x)に
g(x)をq(x)に
置き換えた条件が満たされる時
題意より
p(x)=cosx
q(x)=sinx
となる - よって
p(x)=cosx
∴e^-ax/b・f(x/b)=cosx
∴f(x/b)=e^ax/b・cosx
∴f(x)=e^ax・cosbx
(これがアの正解です) - また
q(x)=sinx
∴e^-ax/b・g(x/b)=sinx
∴g(x/b)=e^ax/b・sinx
∴g(x)=e^ax・sinbx
(これがイの正解です)
難しい式変形です。
医学科の合否を分ける1問です。
受験生としての解説
2023年の九大数学5問で、5番目に簡単な問題です。
問1に関して、g(x)にx=0を代入して矛盾を突くだけなので、不合格者さんでも一定数が正解してきます。よって、合否を分ける1問より少し簡単な問題です。
問2に関して、「微分可能の定義」は不合格者さんには厳しく、合格者さんは乗り越えてくる部分なので、合否を分ける1問です。
問3に関して、与式を「実部と虚部」に分解して「実部=1,虚部=0」を示すことは、不合格者さんの一定数が気づけます。よって、合否を分ける1問より少し簡単な問題です。
問4に関して、難関大特有の複雑な式変形です。合格者さんでも難しいレベルなので、正解できれば他者に差をつける1問となります。
昨年「非常に難しい」と話題になった2022年・大問4と同形式です。しかし、小問1から難しかった昨年と異なり、小問3までは非医歯薬系の受験生さんでも正解できます。部分点を拾いたいところです。小問2で「微分可能の条件」を知らず脱落したとしても、小問3は正解できます。小問4についても、(D)はムリでも(B)は粘れば正解できます。
- 計算:★★★★★(難しい)
- 閃き:★★★★★(強く必要)
- 知識:★★★(普通、極限の公式)
- 総合:★★★★★(難しい)
- 短評:簡単な部分は簡単
大問5

講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、普通程度です。媒介変数による微分積分から面積計算へ進みます。計算の最後に置換積分、sin2乗の積分、sincosの積分があります。いずれも基本レベルなので難しくありません。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。知識の必要性に関して、やや簡単です。媒介変数からの面積計算だけです。
問1に関して、曲線Cに接する直線の内、y軸と平行なものがいくつあるかを答えます。
ポイントは「y軸と平行」です。
「dx/dt=0」となるため、ゴールは近そうです。
- 与式より
x=t+1-cos2t
y=t+sint(0<t<π) - 両辺をtで微分して
dx/dt=1+2sin2t
dy/dt=1+cost - 今、0<t<πにおいて
dy/dt>0より
dx/dt=0となれば題意をみたす
∴ 1+2sin2t=0
∴ sin2t=-1/2
∴ 2t=7π/6,11π/6
∴ t=7π/12,11π/12 - (ⅰ)t=7π/12の時
x=7π/12+1+√3/2 - (ⅱ)t=11π/12の時
x=11π/12+1-√3/2 - よって
(ⅰ)(ⅱ)における接線の接点は異なるため
y軸と平行なCの接線は「2本」となる
(これが正解です)
問2に関して、面積計算です。
- 曲線Cのy≦xの部分
- 直線y=x
で囲まれた図形の面積を答えます。
ポイントは「増減表を書くこと」です。
問1の結果を基に、x・yの増減表を作ると曲線Cを作図できます。作図により形が判るので、積分による面積計算で正解となります。
- 0<t<π において
dy/dt>0より
yは単調増加する - また
xの増減表は以下の通りとなる
| t | 0 | 7/12π | π | ||
| dx/dt | + | 0 | - | ||
| x | ↗ | ↘ |
- 曲線Cと直線y=xの交点において
t+2sin²t=t+sint(0<t<π)
∴ sint=1/2
∴ t=π/6、5π/6 - また、この時
y=5π/6+1/2、π/6+1/2 - よって、求める面積をSとして
S=∫xdy-(π²/3+π/3)
(積分区間:π/6+1/2 → 5π/6+1/2)
=∫(t+2sin²t)(1+cost)dt-(π²/3+π/3)
(積分区間:π/6 → 5π/6)
=∫(t+tcost+2sin²t+2sin²tcost)dt-(π²/3+π/3)
- ∫tcostdt
- =tsint-∫sintdt
- =tsint+cost+C
- ∫2sin²tdt
- =∫(1-cos2t)dt
- =t-sin2t/2+C’
- ∫2sin²tcostdt
- =∫2sin²t(sint)’dt
- =2sin³t/3+C”
C・C’・C”は積分定数
- =[t²/2+tsint+cost+t-sin2t/2+2sin³t/3]-(π²/3+π/3)
=2π/3-√3/2
(これが正解です)
受験生としての解説
2023年の九大数学5問中、2番目に簡単な問題です。
問1に関して、媒介変数の難しくない応用問題なので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
問2に関して、「問題集のコピーの様な問題」なので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
3番目に簡単な大問2より、本問は大きく難易度が下がります。完答しておきたい1問です。「難しい、難しい」と言われる近年の九大数学ですが、非医歯薬系の合格得点率56%を取るだけなら、大問1・大問5のレベルで可能です。
- 計算:★★★(普通)
- 閃き:★(ほぼ不要)
- 知識:★★(やや簡単)
- 総合:★★(やや簡単)
- 短評:完答したい1問
| メイン 得点源 | 簡単ではないが得点したい | 不正解でもOK | 捨て問題 | |
|---|---|---|---|---|
| 大問1 | (1) | |||
| (2) | ||||
| 大問2 | (1) | |||
| (2) | ||||
| (3) | ||||
| (4) | ||||
| 大問3 | (1) | |||
| (2) | ||||
| (3) | ||||
| 大問4 | (1) | |||
| (2) | ||||
| (3) | ||||
| (4)B | ||||
| (4)Dp’(0)=0 | ||||
| (4)Dq’(0)=1 | ||||
| (4)ア | ||||
| (4)イ | ||||
| 大問5 | (1) | |||
| (2) | ||||
| 合計 | 約120点 | 約60点 | 約45点 | 約25点 |
九州大学の数学2022年・令和4年度
大問1

講師としての解説
「空間ベクトル」からの出題です。
計算量・難易度に関して、簡単です。内積の計算が少しあるぐらいです。閃きの必要性に関して、ほぼ不要です。問3の「対象点から最小値を決定する」流れはテクニカルですが、1990年代からずっと定番なので「知識」とみなしてよいでしょう。よって「閃き=頭の良さ」の要素はありません。知識の必要性に関して、普通程度です。90年代から定番の問題です。
問1に関して、条件からnベクトルを求める問題です。
ポイントは「3つの未知数に対し、式を3本立てること」です。問題文が「→nを求めよ」なので、→n=(p,q,r)とおいてp,q,rを求めることになります。よって、式が3本あれば連立方程式でp,q,rが求まる、という流れです。
- aベクトル・nベクトルの直交
- bベクトル・nベクトルの直交
- nベクトルの大きさが1である事
問題文からすぐに立てられそうな式が3本あるので、これを使いましょう。
- →n=(p,q,r)とおくと、問題文の条件より
- |→n|²=p²+q²+r²・・・①
- →n・→a=p+q=0・・・②
- →n・→b=2p+q+r=0・・・③
- ①②③とp>0より
- →n=(p,q,r)=(2/3,-2/3,-1/3)これが正解です。
問2に関して、平面αに関して点Pと対象な点P’の座標を求めます。
ポイントは「→PP’が平面αと直行すること」です。PP’ベクトルがnベクトルと平行になるので、実数kを使ってknベクトルと表します。そして、直交条件の式(内積=0)を立てると「未知数1つ、式1本」となり、これを解けば正解です。
- 線分PP’と平面αの交点をMとすると、点Mは線分PP’の中点となる
- また→PP’//→nより、実数kを用いて
- →PP’=k→nと書ける
- →OM⊥→nより
- →OM・→n=0
- ∴(→OP+→PM)・→n=0
- ∴(→OP+1/2→PP’)・→n=0
- ∴(→OP+k/2・→n)・→n=0
- ∴→OP・→n+k/2|→n|²=0
- ∴4・2/3+(-1)(-1/3)+k/2=0
- ∴k=-6
- ∴→OP’=→OP+→PP’
- =→OP-6→n
- =(4,0,-1)-6(2/3,-2/3,-1/3)
- =(0,4,1)(これが正解です)
問3に関して、「PR+RQ」が最小値となるRの座標を求めます。
ポイントは「対象点P’の活用」です。「PR+RQの最小値」と言われるとよく解りませんが、「P’R+RQの最小値」は点P’・R・Qが一直線に並んだ時と明らかです。そして「P’R=PR」なので・・・
- →OP・→n=3
→OQ・→n=1 - より、→OPと→n、→OQと→nのなす角は鋭角とわかるので、平面αに関して点P・点Qは同じ側に存在する。また、点Pと点Qの平面αからの距離は3:1である。
- 条件よりPR=P’Rであり、P’R+RQが最小となるのはP’・R・Qが一直線の時であるから
- →OR=(→OP’+3→OQ)/(3+1)
- =(3,1,4)(これが正解です)
受験生としての解説
2022年の九大数学5問で1番簡単な問題です。
問1に関して、→n=(p,q,r)とおけば3本の式がすぐに立つので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
問2に関して、「対称点に関する定石」を使うので、不合格者さんの一定数が不正解になります。合格者さんは正解してくるので、合否を分ける1問より少し簡単な問題です。
問3に関して、「対称点の利用による最小値」なので、不合格者さんには難しく、合格者さんは正解してきます。よって、合否を分ける1問です。
本問は、20年以上前には定番となっていた「問題集のコピーの様な問題」そのままでした。「考えて解く」というより「知識問題」なので、才能で劣る学生さんでも知っていれば必ず正解できる1問でした。
九大数学は、全5問から「2完答+3部分点」で非医歯薬系の合格得点率56%を作れます。2022年は大問5が簡単だったので
- 大問5を完答
- 大問1の知識
- 大問2・3・4から部分点
で、才能で劣る学生さんでも九大合格できます。
- 計算:★(簡単)
- 閃き:★★(やや簡単)
- 知識:★★★(普通)
- 総合:★★(やや簡単)
- 短評:30年前から定番
高校偏差値60の高校で落ちこぼれ「1番簡単な国立大学を目指せない」と苦しんでいる学生さんでも取れるようになっています。学区1位の高校で落ちこぼれ「熊本大学を目指せない」と苦しんでいる学生さんなら、余裕を持ってこれ以上のレベルになっています。
大問2

講師としての解説
「整式の除法」と「導関数」からの出題です。
計算量・難易度に関して、やや難しいです。整式の除法に関するテクニカルな計算が続き、導関数の定義に持ち込みます。閃きの必要性に関して、やや強く必要です。知識の必要性に関して、やや深めの知識を要求されています。ただ「微分」できるだけでなく「導関数の定義」に基づいて微分できる事を問われています。
問1に関して、証明問題です。与式を満たす「A、B、CとQ(x)」が存在することを証明します。ポイントは「たった1例だけでも示せばよい」ことです。問題文の指示が「存在することを示せ」なので、1パターンだけ示せば正解となります。
- x^nを(x-α)(x‐β)²で割った時
商をQ(x)、余りをax²+bx+c(a・b・cは実数)とすると - 与式は
x^n=(x‐α)(x‐β)²Q(x)+ax²+bx+c
となる - ここで
ax²+bx+c
=a(x-α)(x‐β)+a(α+β)x-aαβ+bx+c
=a(x‐α)(x‐β)+{a(α+β)+b}x-aαβ+c
=a(x‐α)(x‐β)+{a(α+β)+b}(x‐α)+aα²+bα+c - 以上より、題意を満たすQ(x)・A・B・Cが存在する事を示せた(証明終了)
問2に関して、計算問題です。問1で存在を証明したA・B・Cを具体的に求めます。ポイントは「xに値を代入してA・B・Cだけを残すこと」です。
- 与式にx=αを代入すると
α^n=C(これが正解です) - 与式にx=βを代入すると
β^n=B(β-α)+α^n
∴ B=(β^n-α^n)/(β-α)(これが正解です) - 与式をxで微分すると
nx^n-1=(x-β)²Q(x)+2(x-α)(x-β)Q(x)+(x-α)(x-β)²Q'(x)+A(x-β)+A(x-α)+B - x=βを代入して
nβ^n-1=A(β-α)+B
=A(β-α)+(β^n-α^n)/(β-α) - β-α≠0より
A=nβ^n-1/(β-α) - (β^n-α^n)/(β-α)²
(これが正解です)
問3に関して、Aの極限値を求める問題です。ポイントは「導関数の定義につなぐこと」です。発想の流れは以下のとおりです。
- 問2より「Aの式」の分母が「β-α」になっている
- 問3の問題文で「lim」が使われており「β → α」となっている
- ならば「Aの分子」も「f(β)-f(α)」の形になって
A=lim(f(β)-f(α))/(β-α)=f'(α)
という形になるだろう
- A=1/(β-α){nβ^n-1-(β^n-1+β^n-2α+β^n-3α²+・・・+βα^n-2+α^n-1)}
- =(nβ^n-1ー∑β^n-k・α^k-1)/(β-α)
(∑記号は、k=1→n) - 今、f(β)=nβ^n-1-∑βn-k・α^k-1とおくと
- f(α)=nα^n-1-∑α^n-1=0より
- limA=lim{f(β)-f(α)}/(β-α)
=f'(α)
=n(n-1)α^n-2-∑(n-k)α^n-2
(∑記号はk=1→n-1)
=n(n-1)α^n-2-(n-1){(n-1)+1}/2・α^n-2 - ={n(n-1)α^n-2}/2(これが正解です)
受験生としての解説
2022年の九大数学5問で、3番目に簡単な問題です。
小問1に関して、「存在することを示せ」という頻出ではない出題形式です。不合格者さんには厳しく、合格者さんは乗り越えてくるレベルなので、合否を分ける1問です。
小問2に関して、x=αとβを代入するだけの「BとC」は不合格者さんでも正解してきます。同じ流れで微分が必要になる「A」は合格者さんだけが正解してくるレベルです。
小問3に関して、「問題文で与えられたlimを導関数の定義に結びつけて解く」という難関レベルの式変形なので、合格者さんでも一定数が不正解になります。正解できれば他者に差をつける1問です。
- 計算:★★★★(やや難しい)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:問2だけでも正解しておきたい
高校偏差値60の高校で落ちこぼれ「1番簡単な国立大学を目指せない」と苦しんでいる学生さんでも取れるようになっています。学区1位の高校で落ちこぼれ「熊本大学を目指せない」と苦しんでいる学生さんなら、余裕を持ってこれ以上のレベルになっています。
大問3

講師としての解説
「整数」からの出題です。
計算量・難易度に関して、やや難しいです。問2で合同式、問3で整数問題と、やや煩雑な計算が続きます。閃きの必要性に関して、やや強く必要です。医学科志望の学生さんにとっては「閃き」でなく「知識」ですが、非医歯薬系の学生さんにとっては「閃き」が必要なレベルです。知識の必要性に関して、普通程度です。医学科志望の学生さんにとっては問題丸ごと普通程度の知識、非医歯薬系の学生さんにとっては「普通程度の知識+閃き」を要求される問題です。
問1に関して、証明問題です。与えられた2つの数が「互いに素な整数」である事を示します。ポイントは問題文「互いに素な整数であることを示せ」です。「互いに素ではない」と仮定して計算を進めれば矛盾が発生するはずです。
- n⁴=1+210m²…①に関して
- 右辺が奇数なので左辺のn⁴も奇数となる
- よってnも奇数となる
- ゆえに(n²+1)/2、(n²-1)/2はともに自然数となる
- 今、この2数が互いに素ではないと仮定すると
素数aと自然数b、cを用いて
(n²+1)/2=ab
(n²-1)/2=ac
と表せる - (n²+1)/2-(n²-1)/2=ab-ac
- ∴ 1=a(b-c)
- 上式はaが素数かつb、cが自然数であることに矛盾する
- よって(n²+1)/2と(n²-1)/2は互いに素な整数となる(証明終了)
問2に関して、証明問題です。n²-1が168の倍数である事を示します。ポイントは「168という数値」です。「168=2×2×2×3×7」なので
- 3の倍数かつ
- 7の倍数かつ
- 8の倍数である
ことを示せばよいと解ります。
- (1)よりnは奇数とわかっているので、自然数kを用いて
n=2k-1
と表すことができる - n²-1=(n+1)(n-1)
=2k(2k-2)
=4k(k-1) - ここでk(k-1)は連続する2つの整数の積なので偶数である
- ゆえにn²-1は8の倍数となる
- また①より
- (n²+1)/2・(n²-1)/2=105m²/2…②であり
- 左辺が自然数であることから、右辺も自然数となる。
- よって、m²は偶数であり、ゆえにmは偶数となる。
- 今、自然数pを用いてm=2pと表すと
- ②より
(n²+1)/2・(n²-1)/2
=105・4p²/2
=2×3×5×7×p²…③ - 以下、整数qを用いてnを場合分けして考える
- (ⅰ)n=3qの時
n²+1=3・3q²+1
よりn²+1は3で割り切れない - (ⅱ)n=3q±1の時
n²+1
=9q²±6q+2
=3(3q²±2q)+2
よりn²+1は3で割り切れない - ゆえに③(ⅰ)(ⅱ)より、n²+1は3の倍数ではないため、n²-1が3の倍数となる
- (ⅲ)n=7qの時
n²+1
=7・7q²+1
よりn²+1は7の倍数ではない - (ⅳ)n=7q±1の時
n²+1
=7(7q²±2q)+2
よりn²+1は7の倍数ではない - (v)n=7q±2の時
n²+1
=7(7q²±4q)+5
よりn²+1は7の倍数ではない - (ⅵ)n=7q±3の時
n²+1
=7(7q²±6q+1)+3
よりn²+1は7の倍数ではない - ゆえに③(ⅲ)~(ⅵ)より、n²+1は7の倍数ではないため、n²-1が7の倍数となる
- よって上記より、n²-1は
8の倍数かつ
3の倍数かつ
7の倍数なので
168の倍数となる(証明終了)
問3に関して、「n⁴=1+210m²」を満たす自然数(m,n)の組み合わせを答えます。
ポイントは、自然数Lを用いて「n²-1=168L」と表すことです。問2で「168の倍数」と判明したので、これを活用します。
- (2)の結果より、自然数Lを用いて
n²-1=168Lと表す - ①より
(168L+2)/2・168L/2=2×3×5×7×p²
2L(84L+1)=5p² - よってp²は偶数であり、p=2p’(p’は自然数)とおくことができる
- ∴ 2L(84L+1)=5・4p’²
∴ L(84L+1)=5・2p’² - ここでL=10の時
10(84・10+1)=10p’²
∴ p’²=841
∴ p’=29
∴ m=2p=2(2p’)=116 - また、L=10の時
n²-1=168×10
∴ n=41 - よって、題意を満たす(m,n)の組み合わせとして
(116,41)が存在する(これが正解です)
受験生としての解説
2022年の九大数学5問で、4番目に簡単な問題です。
小問1に関して、「互いに素であることを示せ」なので「互いに素ではない」からの背理法は定番です。不合格者さんには難しく、合格者さんは正解してくるレベルなので、合否を分ける1問です。
小問2に関して、「3の倍数かつ7の倍数かつ8の倍数ある事を示せばよい」という部分は、不合格者さんには難しく、合格者さんは気付けるレベルです。3・7・8と3種類の倍数である事を示す部分が時間を要するため合格者さんでも難しく、正解できれば他者に差をつける1問となっています。
小問3に関して、小問2を正解できた受験生さんにとって「n²-1=168L」とおく事は難しくないでしょう。それ以降もやや思考を要する部分はありますが、小問2を正解できた人なら高確率で乗り越えてきます。よって、小問2とセットで、正解できれば他者に差をつける1問です。
小問3に関する追記。基本的には小問2を応用して「計算で解く」問題ですが、計算ができなかった人でも金庫破り(n=1・2・3・・・と代入していく)で解けます。
問3で金庫破りするコツ
- ①の右辺より、左辺のnは絶対に偶数ではない
- ①において、mが1増えるだけで右辺は大幅に増える
- ①において、nが1増えるだけで左辺は爆発的に増える
上記より、手計算の回数を減らせます。
n=41、m=116が正解です。
練習しておくと、概ねその辺りが正解だろうと見えるようになります。
2022年の様に数学全体が難しい場合「大問1・2・4・5を解き終えて試験時間が大幅に余る」というケースは十分に考えられます。そんな時、時間をムダに消費せず、金庫破りしてでも正解をこそぎ取っておけば不合格が合格にひっくり返る事はよくあります。1150点満点の九大入試で、多くの受験生が「合格ラインの±5点」に集まります。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:問1は正解したい
高校偏差値60の高校で落ちこぼれ「1番簡単な国立大学を目指せない」と苦しんでいる学生さんでも取れるようになっています。学区1位の高校で落ちこぼれ「熊本大学を目指せない」と苦しんでいる学生さんなら、余裕を持ってこれ以上のレベルになっています。
大問4

講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、難しく量はやや多いです。閃きの必要性に関して、強く必要です。理解する事さえ困難な問題文を理解し、それを応用する必要があります。知識の必要性に関して、やや強めに必要です。「平均値の定理を用いて」と提示されています。知っている事が前提の出題です。
問1に関して、証明問題です。与えられた式を導関数の定義に従って導き、目的の式を導出します。難関問題集でよく見かけるタイプですが、短い試験時間で再現するのは大変です。公式の証明を反復練習してきた学生さんに有利な問題です。問2に関して、証明問題です。証明に際して「平均値の定理」を使う事が指示されています。平均値の定理を知っていた場合は、すぐ正解できます。問3に関して、証明問題です。
- f(x)が増加関数なら、xが大きくなるほどf(x)が大きくなり
- それを積分した結果の大小も決まる
という流れです。公式の証明を練習してきた学生さんに有利な問題です。問4に関して、証明問題です。問3で使った②の式はシグマ記号をつけても成り立ちます。その不等式の要素3つを計算していくと、証明すべき③の式が現れ正解となります。
受験生としての解説
2022年の九大数学5問で1番難しい問題です。
非医歯薬系の志望者さんは解かなくても構いません。普段は「大問丸ごと0点だけは防ごう」と指導しておりますが、本問は丸ごと0点でも構いません。「医学科の合否を分ける問題」を見抜いて避け、節約したエネルギーを英語・物理・化学に回し「5教科トータルで合格に特化」した受験を行えば、才能の差を補って九大合格できます。
- 計算:★★★★★(難しい)
- 閃き:★★★★★(難しい)
- 知識:★★★★(やや難しい、平均値の定理が前提)
- 総合:★★★★★(難しい)
- 短評:医学科の合否を分ける問題
高校偏差値60の高校で落ちこぼれ「1番簡単な国立大学を目指せない」と苦しんでいる学生さんでも取れるようになっています。学区1位の高校で落ちこぼれ「熊本大学を目指せない」と苦しんでいる学生さんなら、少し余裕を持ってこれ以上のレベルになっています。
大問5

「微分積分」と「複素数平面」からの出題です。
計算量・難易度に関して、普通程度です。難しくはありませんが、問2まで媒介変数による積分計算が続き、問3から複素数平面の回転計算へ移ります。閃きの必要性に関して、少し必要です。問2までは積分の問題ですが、問3の「回転させた」という文言から「複素数平面」を使う発想が必要です。知識の必要性に関して、普通程度です。積分と複素数平面の基本的な知識で解けます。
問1に関して、証明問題です。「dx/dt<0、dy/dt<0」である事を示します。
ポイントは「実際にtで微分してみること」です。0<t<π/6という狭い区間なので、微分すれば証明完了は近そうです。
- dx/dt=-5sint-5sin5t
=-5(sint+sin5t)
(和積の公式より)
=-10sin3tcos2t - dy/dt=5cost-5cos5t
=5(cost-cos5t)
(和積の公式より)
=10sin3tsin2t - 0<t<π/6より
0<3t<π/2、0<2t<π/3
∴ sin3t>0、cos2t>0、sin2t>0
∴ dx/dt<0(これが正解です)dy/dt>0 - よって
(dy/dt)/(dx/dt)
=dy/dx<0(証明終了)
問2に関して、積分による面積計算です。
ポイントは「媒介変数tによる曲線Cの形」です。これは以下の様に表を作ると明らかです。
| t | 0 | → | π/6 |
| x | 6 | → | 2√3 |
| y | 0 | → | 2 |
- S=2√3・2・1/2+∫ydx(積分区間:2√3→6)
=2√3+√y・dx/dt・dt(積分区間:π/6→0)
=2√3+5∫(5sin²t+4sin5tsint-sin²5t)dt(積分区間:0→π/6) - ここで
sin²t=(1-cos2t)/2
sin5tsint=-(cos6t-cos4t)/2
sin²5t=(1-cos10t)/2
なので - S=2√3+5[2t-5/4・sin2t-1/3・sin6t+1/2・sin4t+1/20・sin10t]
(カッコの区間:0→π/6)
=5π/3(これが正解です)
問3に関して、曲線Cがx軸に関して対称であることを示します。また、C上の点を原点中心で反時計回りにπ/3だけ回転させた点がC上にあることを示します。
ポイントは「実際に動かしてみること」です。「x軸対称」ならば、ある点の構成要素に「-1」をかければ「x座標はそのまま、y座標は-1倍」ということが起こるはずです。「π/3だけ回転させた点」は曲線Cの方程式を満たすはずです。
- x(t)=5cost+cos5t
y(t)=5sint-sin5t
とおくと - x(-t)=5cost+cos5t=x(t)
y(-t)=-5sint+sin5t=-y(t) - よって区間0≦t≦πにおいて
点(x(t),y(t))と点(x(-t),y(-t))はx軸対称であるから
曲線Cはx軸対称な曲線である(証明終了)
続いて「π/3だけ回転させた点」に関して
- 曲線C上の点(x(t),y(t))を原点中心・反時計回りにπ/3だけ回転させた点を(X,Y)とおく
- X+Yi
={x(t)+y(t)i}(cosπ/3+isinπ/3)
=x(t)cosπ/3-/3+i{x(t)sinπ/3+y(t)cosπ/3}
となる - ここで
X=(5cost+cos5t)cosπ/3-(5sint-sin5t)sinπ/3
=5(costcosπ/3-sintsinπ/3)+cos5tcosπ/3+sin5tsinπ/3
=5cos(t+π/3)+cos(5t-π/3)
=5cos(t+π/3)+cos(5t+5π/3-2π)
=5cos(t+π/3)+cos5(t+π/3)
=x(t+π/3) - また
Y=(5cost+cos5t)sinπ/3+(5sint-sin5t)cosπ/3
=5(costsinπ/3+sintcosπ/3)+cos5tsinπ/3-sin5tcosπ/3
=5sin(t+π/3)-sin(5t-π/3)
=5sin(t+π/3)-sin(5t+5π/3-2π)
=5sin(t+π/3)-sin5(t+π/3)
=y(t+π/3) - 上記より、移動後の点(X,Y)は曲線C上の点である(証明終了)
問4に関して、作図問題です。曲線Cの概形を描きます。
ポイントは「問3の活用」です。
- 曲線Cはx軸対称
- 曲線Cは反時計回りにπ/3ずらしても曲線C
と判っているので、ほんの1部分さえ描ければ、曲線C全体につなげることができます。
- t:0 → π/6の時
x:6 → 2√3
y:0 → 2
であり - d²y/dx²
=d/dx(dy/dx)
=dt/dx・d/dt(dy/dx)
=dt/dx・d/dt(dy/dt・dt/dx)
=1/(-10sin3tcos³2t)・d/dt{10sin3tsin2t/(-10sin3tcos2t)}
=1/(-10sin3tcos³2t)・d/dt(-tan2t)
=1/(-10sin3tcos³2t)・(-2/cos²2t)
=1/5sin3tcos³2t>0
なので - 曲線Cのグラフの一部は
点(2√3,2)から点(0,6)にかけて
下に凸な曲線となる - 問3より、曲線Cはx軸対称なので
上記をx軸で反転したものも曲線Cの一部となる - 問3より、曲線C上の点を
原点中心・反時計回りにπ/3移動させた点も曲線C上にあるので
上記の曲線を原点中心・反時計回りに
π/3ずつ5回コピーしたもの(計6回分)が
正解の図形となる
九州大学としては珍しい「私立中学風の図形」でした。
受験生としての解説
2022年の九大数学5問で、2番めに簡単な問題です。
小問1に関して、微分して大小関係を調べるだけなので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問2に関して、簡単な面積計算なので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問3に関して、簡単な問題ではありませんが「問題集のコピーの様な問題」です。練習しておけば必ず解けるようになる問題なので、不合格者さんには厳しく、合格者さんは正解してきます。よって、合否を分ける1問です。
小問4に関して、小問3が正解できた学生さんにとっては難しくないレベルです。よって、小問3とセットで、合否を分ける1問です。
媒介変数は九大数学の中でも解きやすい問題が多いので、非医歯薬系の受験生さんでも乗り越えてください。他から点数を取るより楽です。
大問1・大問5「問題集のコピーの様な問題」を確実に正解しておけば、大問4の様な難問を解かずとも非医歯薬系の合格得点率56%を超える事ができます。
- 計算:★★★(普通)
- 閃き:★★(やや簡単)
- 知識:★★★(普通)
- 総合:★★(やや簡単)
- 短評:完答したい1問
高校偏差値60の高校で落ちこぼれ「1番簡単な国立大学を目指せない」と苦しんでいる学生さんでも取れるようになっています。学区1位の高校で落ちこぼれ「熊本大学を目指せない」と苦しんでいる学生さんなら、少し余裕を持ってこれ以上のレベルになっています。
九州大学の数学2021年・令和3年度
大問1

講師としての解説
「空間図形」からの出題です。
計算の量・難易度に関して、普通程度です。分数計算・ルート・平方完成で正解できます。閃きの必要性に関して、やや少なめです。問1を解く際に、四面体の体積を2パターンで表しイコールでつなぐ程度です。知識の必要性に関して、普通程度です。難関大限定「点と平面の距離の公式」の使用が模範解答となっています(教科書の範囲外です)
問1に関して、体積計算です。ポイントは「体積を2パターンで表すこと」です。
- 四面体OABCに内接する球の半径をrとすると
- 球の中心点I(r,r,r)となる
- ここで四面体の体積をVと置くと
V=r×(四面体の4つの面)×1/3
=r/3・(△OAB+△OBC+△OCA+△ABC)
=r/3・(1/2+1+1+3/2)
=4r/3…①
となる - 一方、四面体の体積Vは
底面:△OAB
高さ:辺OC
とみなし - V=△OAB×OC×1/3
=1/3…②
とも表せる - ①=②より
r=1/4(これが正解です)
問2に関して、球が平面ABCと交わった際にできる「円の面積の最大値」を答えます。
ポイントは「半径の最大値を求めること」です。「面積の最大値」を要求されていますが、「面積=半径²×π」なので、欲しいのは「半径の最大値」です。
- 球の中心点Iから平面ABCに下ろした垂線の足を点Hとし
IH=hとおく - 今、点Hは平面ABC上の点なので
→IH=→IA+α→AB+β→AC
=(1-r-α-β,-r+α,-r+2β)…③
を満たす実数α・βが存在する - さらに→IHは、→ABおよび→ACに直交するので
→IH・→AB=0
∴ 2α+β-1=0
→IH・→AC=0
∴ α+5β-r-1=0
となる
∴ α=(4-r)/9,β=(2r+1)/9…④ - ③④より
→IH=(2-5r)/9・(2,2,1)
であり - |→IH|=|2-5r|/3=h
となる - 球と平面ABCが交わる条件は
点Iから平面ABCへの垂線|→IH|より
球の半径rが大きいことなので
|2-5r|/3<r
∴ (4r-1)(r-1)<r
∴ 1/4<r<1…⑤ - この時、球と平面ABCの交わりによる
円の半径をRとおくと
三平方の定理より
R=√(r²-h²)
=√{-16/9・(r-5/8)²+1/4}…⑥ - よって⑤⑥より
Rが最大となるのは
r=5/8
の時であり
R=1/2
この時、円の面積は最大値
πR²=π/4(これが正解です)
となる
受験生としての解説
2021年の九大数学5問で、2番めに簡単な問題です。
小問1に関して、四面体の体積を
- 底面積×高さ÷3
- 内接球の半径×表面積÷3
という2通りで表すだけなので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問2に関して、細かく長い計算が続くため、基礎力を問われる1問です。不合格者さんには厳しく、合格者さんは乗り越えてくるレベルなので、合否を分ける1問です。
九大数学は5つの大問から「2完答+3部分点」という形を作れば、非医歯薬系の合格得点率56%に届きます。2021年は、大問1・大問3を確実に完答しておけば、難しい大問4・大問5を解かずとも九大合格できます。
- 計算:★★★(普通)
- 閃き:★★(やや簡単)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:完答したい1問
大問2

講師としての解説
「複素数平面」からの出題です。
計算の量・難易度に関して、やや簡単です。判別式、解と係数の関係、複素数の計算など、基本的なもので完答できます。閃きの必要性に関して、普通程度に必要です。複素数平面乗で実軸対称な図形を扱います。知識の必要性に関して、普通程度です。方程式の解が複素数の場合は「共役複素数も解となる」事などです。
問1に関して、与式が「実数解を持たない条件」を求めます。
ポイントは「判別式<0」です。cosθやtanθがあるとはいえ、与式はxの二次方程式です。よって「実数解を持たない ↔ 判別式<0」と持ち込めます。
- x²-(4cosθ)x+1/tanθ=0…①
- 実数解を持たない条件なので
判別式Dとして
D/4=4cos²θ-1/tanθ<0…② - 今、0<θ<π/4よりtanθ>0
ゆえに②の両辺にtanθをかけて
4cos²θtanθ-1<0
∴ 4sinθcosθ<1
∴ 2sin2θ<1
∴ sin2θ<1/2…③ - 0<θ<π/4より
0<2θ<π/2なので
③より
0<2θ<π/6
∴ 0<θ<π/12(これが正解です)
「判別式<0」から「θの範囲」に持ち込むだけなので、不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、問1の虚数解が描く「円の中心」を答えます。
ポイントは点A・点Bを表す複素数が「共役の関係」にある事です。点A・点Bは「実軸対称」で存在するので、点Cは実軸上に存在します。
- 問1の虚数解をα、βとおくと
β=α*となる(*はバーを表す) - 解と係数の関係より
α+β=α+α*=4cosθ…④
αβ=αα*=1/tanθ…⑤ - 3点A・B・Oの条件より
|α-γ|=|γ|かつγは実数
∴|α-γ|²=|γ|²
∴(α-γ)(α*-γ)=γ²
∴αα*-(α+α*)γ=0
∴1/tanθ -4cosθ・γ=0(∵④⑤)
∴γ=1/4sinθ…⑥
(これが正解です)
- 図形をヒントにした立式
- 複素数計算の処理(両辺2乗)
- 解と係数の関係の活用
少しだけ難しい要素が3連発ということで、不合格者さんには厳しく、合格者さんは正解してきます。
よって、合否を分ける1問です。
問3に関して、問2の条件に「直角三角形」を加えた時の「tanθの値」を答えます。
ポイントは「点Cが線分ABの中点」です。
- 条件より、点Cは線分ABの中点になるので
γ=(α+β)/2
=(α+α*)/2…⑦ - ④⑥⑦より
1/(4sinθ)=2cosθ
∴1=8sinθcosθ
∴8tanθcos²θ=1
∴8tanθ/(1+tanθ)=1
∴tan²θ-8tanθ+1=0
∴tanθ=4±√15 - 今
tanπ/12
=tan(π/3-π/4)
=(√3-1)/(1+√3)
=2-√3
であり、虚数解を持つ条件より
0<θ<π/12
なので
0<tanθ<2-√3 - よって
tanθ=4-√15(これが正解です)
問2が正解できた方には、同じ流れなので難しくありません。
よって、問2とセットで、合否を分ける1問です。
受験生としての解説
2021年の九大数学5問中、1番簡単な問題です。
大問4・大問5に比べ簡単なので、完答を目指したいところです。小問2がやや難しいですが、小問3の正解がセットになるタイプなので、ここは頑張りどころです。
- 計算:★★(やや簡単)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問3

講師としての解説
「微分積分」からの出題です。
計算の量・難易度に関して、普通程度です。増減表を書き、極限を調べ、部分積分で解きます。閃きの必要性に関して、普通程度です。問1において、x・y・tが自由に動き回るので基準を見つける必要があります。知識の必要性に関して、やや少ないです。存在条件に関する知識が必要です。
問1に関して、与式を満たす(x,y)の集合を作図します。
ポイントは「基準を見つけること」です。
- x・y・tと変数が3つある一方
- 与えられる不等式はわずか1本
これが本問の難しさの正体です。問題文に「x・yの集合を図示せよ」と書いてあるので、計算の最終形は「x・yの式」となります。つまり「tの関数」と考え「tを基準」にすればよいと解ります。
- f(t)=e^t-xtとおくと
f'(t)=e^t-x - (ⅰ)x<0の時
f'(t)>0となるためf(t)は単調増加する
t→-∞とした時に
limf(t)=-∞
となるため
全ての実数tに対して(※)が成り立つ(x,y)は存在しない - (ⅱ)x=0の時
f(t)=e^tより
全ての実数tで(※)が成り立つ条件は
y≦0 - (ⅲ)x>0の時
f(t)の増減表は以下の様になる
| t | logx | ||
| f'(t) | - | 0 | + |
| f(t) | ↘ | x(1-logx) | ↗ |
- よって、全ての実数tで(※)が成り立つ条件は
y≦x(1-logx) - (ⅰ)~(ⅲ)より
全ての実数tで(※)が成り立つ条件は
x=0 かつ y≦0
または
x>0 かつ y≦x(1-logx)
となる
以下、作図のためにy=x(1-logx)の形状を明らかにします
- g(x)=x(1-logx)とおくと
g'(x)=-logx
増減表は以下の様になる
| x | 0 | 1 | ||
| g'(x) | + | 0 | - | |
| g(x) | ↗ | 1 | ↘ |
- x→+0において
limg(x)=0 - x→∞において
limg(x)=-∞ - 以上を作図したものが正解となる
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
合否を分ける1問です。
問2に関して、問1で求めた図形に関し「x=0かつy≦0」を満たすものをSとした時、「Sをx軸のまわりに1回転させてできる立体の体積」を答えます。
- 求める体積をVとすると
V=∫π{g(x)}²dx(積分区間は1→e)
=π∫x²(1-logx)²dx
(以下、部分積分で解きます)
=π{[x³/3(1-logx)²]-∫x³/3・2(1-logx)(-1/x)dx}
=π{-1/3+2/3∫x²(1-logx)dx
(もう1回、部分積分するだけなので計算省略します)
=(2e³-17)/27
(これが正解です)
簡単な体積計算なので、不合格者さんでも正解してきます。
しかし、本問に参加するには「問1の正解」が必要です。
よって、問1とセットで、合否を分ける1問です。
受験生としての解説
2021年の九大数学5問で、3番目に簡単な問題です。
小問2が簡単なので、小問1の結果で「満点か0点」に分かれる怖い1問です。
比較的簡単な大問1~大問3を完答できれば、難しい大問4・大問5はほとんど得点できずとも、非医歯薬系の合格得点率56%を超えられます。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★(やや少ない)
- 総合:★★★(普通)
- 短評:本当は難しくない
大問4

講師としての解説
「微分」と「複素数平面」からの出題です。
計算量・難易度に関して、やや難しいです。複素数の煩雑な計算が続きます。最後は6乗根が出てきます。閃きの必要性に関して、やや強く必要です。問題文で与えられた解き方を理解し、その場で応用するタイプです。事前の準備がしにくい、頭の良い人ほど有利なパターンです。知識の必要性に関して、普通です。解き方は問題文で与えられるため、必要な知識は普通程度です。
問1に関して、証明問題です。n=2の時に「どのようなα、β、f(x)も平均値の性質を持つ」ことを示します。
ポイントは「言われた通りに実行すること」です。「平均値の性質」を理解するための誘導問題なので、「n=2」を代入すれば簡単になるはずです。
- 与式にn=2を代入すると
f(x)=a₂x²+a₁x+a₀
f'(x)=2a₂x+a₁…① - ゆえに
{f(β)-f(α)}/(β-α)
={a₂(β²-α²)+a₁(β-α)}/(β-α)
=a₂(α+β)+a₁…② - 今、①において
x=(α+β)/2
とすると①=②となる - この時
x=(α+β)/2は線分αβの中点であり
γの条件を満たすので
どのようなα、β、f(x)も平均値の性質をもつ
(証明終了)
言われた通りに実行すれば正解が出るので、不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、証明問題です。
- α=1-i
- b=1+i
- f(x)=x³+ax²+bx+c
上記3つが「平均値の性質」を持つための「実数a、b、cに関する必要十分条件」を答えます。
ポイントは「部品に分け、バラバラに考えること」です。問1の「n=2」に比べ、問2は条件が複雑になりました。この様な場合、{f(β)-f(α)}/(β-α)=f'(γ)を
| f(β)-f(α) | 左辺・分子 |
| β-α | 左辺・分母 |
| f'(γ) | 右辺 |
と分解し、1個ずつ丁寧に計算すると上手くいきます。
- 条件より
α+β=2、αβ=2 - f(β)-f(α)
=β³-α³+a(β²-α²)+b(β-α)
=(β-α){(α+β)²-αβ+a(α+β)+b} - {f(β)-f(α)}/(β-α)
=(α+β)²-αβ+a(α+β)+b
=2²-2+2a+b
=2a+b+2 - また
f’(x)=3x²+2ax+b…④ - 上記が平均値の性質を持つ時
③=④より
2a+b+2=3γ²+2aγ+b
∴ 3γ²+2aγ-2a-2=0
∴ γ={-a±√(a²+6a+6)}/3…⑤ - 今、α=1-i、β=1+iの実部がいずれも1なので
⑤のγが線分αβ上にあるためには
(⑤の実部)=-a/3=1
∴a=-3
が必要となる - この時、⑤にa=-3を代入すると
γ=1±√3i/3となり
実数b,cの値に関わらず
平均値の性質を十分に満たす - よって、求める必要十分条件は
a=-3 かつ 任意の実数b、c
(これが正解です)
「部品ごとに分解」して正解を導くことは、不合格者さんには難しく、合格者さんは乗り越えてきます。
その後「必要十分条件」につないで締めくくる部分は、合格者さんでも難しいです。
よって、正解できれば他者に差をつける1問です。
問3に関して、証明問題です。
- α=(1-i)/√2
- β=(1+i)/√2
- f(x)=x⁷
上記3つが平均値の性質を「もたない」ことを示します。
ポイントは「2種類の方法で点γを表すこと」です。
- 条件より
f'(x)=7x⁶
α=cos(-π/4)+isin(-π/4)
β=cosπ/4+isinπ/4 - ド・モアブルの定理より
α⁷=cos(-7/4・π)+isin(-7/4・π)=β
β⁷=cos7π/4+isin7π/4=α - 上記より
{f(β)-f(α)}/(β-α)
=(α-β)/(β-α)
=-1…① - 平均値の性質を持つ時
①=f'(γ)
となるため
7γ⁶=-1
∴ γ⁶=-1/7=1/7・(cosπ+isinπ)
∴ γ=1/⁶√7・(√3/2+i/2)…(A) - ところで、γが線分αβ上の点と仮定すると
γ=(1+ki)/√2(-1≦k≦1)…(B)
と表すことができるが
7<8=2³=(√2)⁶
∴ ⁶√7<√2
∴ 1/⁶√7>1/√2
より(A)と(B)が一致することはありえず矛盾する - よって、平均値の性質を持たないことを証明できた
(証明終了)
合格者さんでも難しいレベルです。
ただし「医学科の合否を分ける1問」と言うほど難しくもありません。
よって、正解できれば他者に差をつける1問です。
受験生としての解説
2021年の九大数学5問で2番めに難しい問題です。
非医歯薬系の受験生さんであれば、小問3は解けなくても構いません。比較的簡単な大問1~大問3で多めに得点を取り、難しい大問4・大問5から部分点を取れば合格ラインに届きます。
本問を解くために数学の難しい問題を練習するより、英語・物理・化学の基礎を固めた方が合格に近づけます。5教科トータルで考え「できるだけ簡単に合格する」という発想を持つと良いです。
ただし、小問3も部分点は狙えます。例えば、小問2と同様に条件式を分解し、部品ごとに計算することは医学科以外の受験生さんでもできます。特にド・モアブルの定理は、ここで初めて使うことになるので「α⁷=β、β⁷=α」を答案用紙に書いておけば、部分点になる可能性は高いです。
- 計算:★★★★(やや難しい、煩雑)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:小問2まででよい
大問5

講師としての解説
「整数」からの出題です。
計算量・難易度に関して、やや難しいです。場合の数・確率でよく使う「C」の計算と不等式の応用です。閃きの必要性に関して、強く必要です。医学科用の超難関問題集で訓練した人には「知識」と言える範囲ですが、非医歯薬系の受験生さんは対策しにくい問題です。知識の必要性に関して、普通です。コンビネーション、不等式、場合分け、普通の知識を使います。
問1に関して、証明問題です。自然数n,kが2≦k≦n-2を満たす時「nCk>n」であることを示します。
ポイントは「nCkが『n×(1より大きいものの集合体)』である」ことです。
- 2≦k≦n-2…①において
nCk=n!/{(n-k)!k!}
=n(n-1)・・・(n-k+1)/{k(k-1)・・・2・1}
=n・(n-1)/k・(n-2)/(k-1)・・・(n-k+1)/2…② - ①より
n-1>n-2≧k
n-2>k-1
・・・
n-k+1>2 - ゆえに
(n-1)/k>1
(n-2)/(k-1)>1
・・・
(n-k+1)/2>1 - よって
②>nとなるため
nCk>n
となる(証明終了)
小問1なので、なるべく正解したいですが、合格者さんでも難しいレベルです。
よって、正解できれば他者に差をつける1問です。
問2に関して、pを素数とした時、k≦nを満たす自然数の組(n,k)でnCk=pとなるものを答えます。
ポイントは「問1の利用」です。『2≦k≦n-2』がゴッソリ消えて『k=1,n-1,n』の3パターンだけ考えれば正解できます。
- nCk=p…③において
- (ⅰ)2≦k≦n-2の時
問1の結果と③より
n<p…④
となる - また③より
n!/{k!(n-k)!}=p
∴ n!=p・k!(n-k)!…⑤ - ⑤の右辺はpの倍数であるが
⑤の左辺は④よりpの倍数ではなため
⑤は矛盾している - よって、2≦k≦n-2において
題意を満たすkは存在しない - (ⅱ)k=1の時
③より
nC₁=p
∴ n=p - (ⅲ)k=n-1の時
③より
nCn-1=p
∴ n=p - (ⅳ)k=nの時
③より
nCn=p
∴ p=1
となるが、これはpが素数であることに矛盾する - よって(ⅰ)~(ⅳ)より
題意を満たす自然数の組み合わせは
(n,k)=(p,1)(p,p-1)
(これが正解です)
このタイプの難問は、ひとまず簡単な数値を代入すると良いです。例えば「k=1、k=n」を代入すると、式が極端な形になって法則性が見えてきます。
難問ですが「医学科専用」と言う程ではありません。
しかし、2021年の九大数学で突出して難しい1問です。
よって「医学科の合否を分ける問題」とみなし、非医歯薬系の受験生さんは解けなくて構いません。
受験生としての解説
2021年の九大数学5問で1番難しい問題です。
配点が50点もありますから白紙で提出せず、思いついた事を何かしら書いて部分点を拾ってください。
本問にはあまり深い入りせず、簡単な大問1~大問3を解けば、非医歯薬系の合格ラインを超えられます。
また、大問4は「時間をかけるほど正解に近づける」作りなので、こちらに時間を回すのも良いでしょう。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや難しい)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:部分点ねらい
九州大学の数学2020年・令和2年度
大問1

講師としての解説
「微分」からの出題です。
計算に関して、やや簡単です。分数の積分があります。閃きの必要性に関して、ほぼ不要です。微分して、増減表を書いて、作図するだけです。知識の必要性に関して、少し必要です。問題文の「直線が存在する条件」を「接線の式が成り立つようなtが存在する条件」と置き換える定石です。
誘導となる小問はありません。与式に接する直線が存在するような「定数aの値の範囲」を答えます。
ポイントは「先に接線の方程式を立てること」です。
- y=e^-x – e-^-2x…①
より
y’=-e^-x + 2e^-2x…② - x=tにおける①の接線の方程式は
y-(e^-t -e^-2t)=(-e^-t + 2e^-2t)(x-t) - この直線が(a,0)を通るとすると
-(e^-t – e^-2t)=(-e^-t + 2e^-2t)(a-t)
∴ (e^t -2)(a-t)=(e^t-1)…③
③を満たす「tが存在するようなaの範囲」が正解なので、これを求めます。
- t=log2の時③は成り立たないので
e^t-2≠0
ゆえに③より
a=t+1+1/(e^t-2) - 今、f(t)=t+1+1/(e^t-2)とおくと
f'(t)=1-e^t/(e^t-2)²
=(e^t-1)(e^t-4)/(e^t-2)²
増減表を描いて「y=f(t)のグラフの形」を明らかにします。
| t | 0 | log2 | 2log2 | ||||
| f'(t) | + | 0 | – | / | – | 0 | + |
| f(t) | ↗ | 0 | ↘ | / | ↘ | 3/2+2log2 | ↗ |
- t→∞:limf(t)=∞
t→-∞:limf(t)=-∞
t→log2+0:limf(t)=∞
t→log2-0:limf(t)=-∞
「y=aのグラフ」は横一直線です。2つのグラフが交わる範囲が正解なので
- 求めるaの値の範囲は
a≦0,3/2+2log2≦a
(これが正解です)
微分して接線の方程式を立て、増減表を描くだけなので、不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
受験生としての解説
2020年の九大数学5問で、1番簡単な問題です。
九大数学は全5問から「2完答+3部分点」で非医歯薬系の合格得点率56%を作れます。本問を完答しておけば、残り4問から「1完答+3部分点」となるため、完答を目指したい1問です。
- 計算:★★(やや簡単)
- 閃き:★(ほぼ不要)
- 知識:★★★(普通)
- 総合:★★(やや簡単)
- 短評:完答したい1問
高校偏差値60の高校で落ちこぼれ「1番簡単な国立大学を目指せない」と苦しんでいる学生さんでも取れるようになっています。学区1位の高校で落ちこぼれ「熊本大学を目指せない」と苦しんでいる学生さんなら、少し余裕を持ってこれ以上のレベルになっています。
大問2

講師としての解説
「高次方程式」と「整数」からの出題です。
計算に関して、やや難しいです。前半では因数分解によるやや煩雑な計算があり、後半では4本の合同式による煩雑な計算があります。閃きの必要性に関して、やや強く必要です。複素数から急に整数問題へスイッチしているので、適応する必要があります。また、絶対値の応用があります。知識の必要性に関して、普通程度です。虚数解の性質、合同式の知識が必要です。
問1に関して、与式のc,dをa,bを用いて表します。
ポイントは「虚数解の性質」です。
複素数が方程式の解だった時は「その共役複素数も解である」という性質を使います。「解である」という事は「因数分解できる」という事です。因数分解から「はみ出た項」は全て0となるので、c・dをa・bで表すことができます。
- 以下、複素数の表現において
「*」を「 ̄」の代わりに用いる
(例:|a|²=aa*) - w=(1+√3i)/2 とおくと
wはf(x)=0の解なので
共役な関係のw*も解となる - よって、f(x)は
(x-w)(x-w*)=x²-x+1
で割り切れる - 今
f(x)=x⁴+ax³+bx²+cx+d
=(x²-x+1){x²+(a-1)x+a+b}+(b+c-1)x-a-b+d
より
b+c-1=0、-a-b+d=0
となる - よって
c=1-b、d=a+b
(これが正解です)
不合格者さんには厳しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問2に関して、整数問題となります。
- f(1)を
7で割ると1余り
11で割ると10余る - f(-1)を
7で割ると3余り
11で割ると10余る - |a|≦40
|b|≦40
というf(x)に関し、f(x)=0の解を全て求めます。
ポイントは「合同式の活用」です。
問1の結果より、4本の合同式を立てることができます。これを解いていくとa・bの候補が複数挙がります。しかし、問題文で「a・bの絶対値は40以下」と定めてあるため、1つに絞れて正解・・・という流れです。
- f(x)に問1の結果を代入して
c,dを消去すると
f(x)=x⁴+ax³+bx²+(-b+1)x+a+b - x=1,-1を代入して
f(1)=2a+b+2
f(-1)=3b - ここで問題文の条件より
2a+b+2≡1(mod7)…①
3b≡3(mod7)…②
2a+b+2≡10(mod11)…③
3b≡3(mod11)…④
となる
では、まずbから求めていきましょう。
- ②に関して
3と7は互いに素なので
b≡1(mod7)
よって整数kを用いて
b=7k+1…⑤
と書ける - ⑤を④に代入すると
3(7k+1)≡10(mod11)
∴ 21k≡7≡84(mod11)
21と11は互い素なので
k≡4(mod11)
よって整数lを用いて
k=11l+4…⑥
と書ける - ⑤⑥より
b=7(11l+4)+1
=77l+29…⑦ - 今、|b|≦40より
⑦を満たす整数lは0だけである
よって
b=29
同じ方法でaも求まります。
- b≡1(mod7)を①に代入して
2a+3≡1(mod7)
∴2a≡-2(mod7)…⑧ - ⑧に関して
2と7は互いに素なので
a≡-1(mod7)
よって整数mを用いて
a≡7m-1…⑨
と書ける - ⑨とb=29を③に代入すると
2(7m-1)+29+2≡10(mod11)
∴14m≡-19≡14(mod11)
14と11は互いに素なので
m≡1(mod11)
よって整数nを用いて
m=11n+1…(10)
と書ける - ⑨(10)より
a=7(11n+1)-1
=77n+6…(11) - 今、|a|≦40より
(11)を満たす整数nは0だけである
よって
a=6
aとbが求まったので、最後の締めくくりです。
- 与式にa=6,b=29を代入すると
f(x)=(x²-x+1)(x²+7x+35)
よって、f(x)=0の解は
x=(1±√3i)/2 , (-7±√91i)/2
(これが正解です)
「医学科の合否を分ける難問」と言うほど難しくありません。
しかし、2020年の九大数学で突出して難しい1問です。
他に解きやすい問題がたくさんあるので、まずそちらに時間を回しましょう。
受験生としての解説
2020年の九大数学で1番難しい問題です。
小問1「高次方程式」は問題集でよく見かけるパターンなので、非医歯薬系の志望者さんでも正解したいところです。後半の合同式も決して「医学科以外は解けない」というレベルではありません。しかし、2020年は他に解きやすい問題がたくさんあるので、まずそちらに時間を使いましょう。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:小問1まで正解したい
大問3

講師としての解説
「空間ベクトル」からの出題です。
計算の量・難易度に関して、普通程度です。a,b,c3つのベクトルによる「内積・ベクトルの大きさ・なす角」を扱うので、やや煩雑な計算が続きます。閃きの必要性に関して、やや強めに必要です。「四面体の中心」と言える点が与えられていないため、自分で設定し、証明する必要があります。知識の必要性に関して、普通程度です。ベクトルの基本知識で解けます。
問1に関して、直線OBと直線CAのなす角θ(0≦θ≦π/2)を求めます。
ポイントは「内積」です。ベクトルで「なす角」と言われたら内積です。「各辺の中点を結ぶ直線」が直交する条件を使うと「内積=0」の式が3本立ちます。これを解くと正解・・・という流れです。
- 以下の様に、各辺の中点を設定する
| 辺 | 中点 |
|---|---|
| OA | P |
| OB | Q |
| OC | R |
| BC | S |
| CA | T |
| AB | U |
まず、ベクトル問題を解くための材料(=大きさ・内積)を集めます。
- 以下
aベクトルは「a」
bベクトルは「b」
cベクトルは「c」
で表現する - →PS=→OS-→OP
=(b+c-a)/2
同様にして
→QT=(c+a-b)/2
→RU=(a+b-c)/2 - l⊥m、m⊥n、n⊥lより
→PS・→QT=0
→QT・→RU=0
→RU・→PS=0 - ゆえに
(b+c-a)(c+a-b)=0
(c+a-b)(a+b-c)=0
(a+b-c)(b+c-a)=0 - ゆえに
|c|²=|a-b|²=AB²=5…①
|a|²=|b-c|²=BC²=3…②
|b|²=|c-a|²=CA²=4…③ - ゆえに
|c|=√5
|a|=√3
|b|=2
これで材料の1つ「大きさ」がそろいました。次は「内積」を求めます。
- ①②③より
|a-b|²=|a|²-2a・b+|b|²=5
|b-c|²=|b|²-2b・c+|c|²=3
|c-a|²=|c|²-2c・a+|a|²=4 - ゆえに
a・b=1
b・c=3
c・a=2
これで2つ目の材料「内積」がそろいました。
では、いよいよ問題を解きにかかります。
- 内積の式より
→OB・→CA
=|→OB||→CA|cosθ - ゆえに
cosθ=(→OB・→CA)/|→OB||→CA|
=b・(a-c)/2・2
=(1-3)/4
=-1/2 - よって
θ=2π/3…④
となるが、これは題意の
0≦θ≦π/2
に反する - よって
θ=π-④
=π/3(これが正解です)
となる
材料(=大きさ・内積)を集めて「なす角」を求める定番です。
よって、不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問2に関して、外接球の半径を答えます。
ポイントは「外接球の中心を自分で設定する」ことです。
問題文の中に「外接球の中心になりそうな点」はありません。しかし「直線l、m、n」が球の中心を通りそうな気はします。
- 線分PSの中点をDとおくと
→OD=(→OP+→OS)/2
=(a+b+c)/4
この点Dが「おそらく外接球の中心だろう」と決めつけて、解き進めます。
- |4→OD|²=|a+b+c|²
=|a|²+|b|²+|c|²+2a・b+2b・c+2c・a
=3+4+5+2・1+2・3+2・2
=24
∴|→OD|²=24/16=3/2
∴|→OD|=√6/2
「線分OD=√6/2」と判りました。問1で集めた「材料」を使い「AD=BD=CD=√6/2」を示せば正解となります。後はひたすら計算のみです。
- 4→AD=4(→OD-→OA)=-3a+b+c…⑤
4→BD=4(→OD-→OB)=a-3b+c…⑥
4→CD=4(→OD-→OC)=a+b-3c…⑦ - ⑤より
|4→AD|²=|-3a+b+c|²
=9|a|²+|b|²+|c|²-6a・b+2b・c-6c・a
=24
∴|→AD|=√6/2 - ⑥より
|4→BD|²=|a-3b+c|²
=|a|²+9|b|²+|c|²-6a・b-6b・c+2c・a
=24
∴|→BD|=√6/2 - ⑦より
|4→CD|²=|a+b-3c|²
=|a|²+|b|²+9|c|²+2a・b-6b・c-6c・a
=24
∴|→CD|=√6/2 - よって、点Dから4点O・A・B・Cまでの距離が
全て√6/2と示せたので
求める球の半径は√6/2(これが正解です)
となる
球の中心が与えられてないため、見た目より難しい問題です。
合格者さんでも一定数の不正解が出るレベルなので、正解できれば他者に差をつける1問です。
受験生としての解説
2020年の九大数学5問で、2番めに難しい問題です。
小問1の「なす角」を内積で求める問題は定番です。正解したい問題です。小問2は難しいですが「医学科・臨床科以外は解かなくてよい」と言うほどの難問でもありません。しかし、2020年は大問1・大問4・大問5が得点しやすいので、まずそちらを優先した方が良いでしょう。
九大数学は大問5つから「2完答+3部分点」で非医歯薬系の合格得点率56%を作れるので「できるだけ簡単に合格する」という発想を持ってください。
大問4がサイコロ問題(時間をかけるほど正解に近づけるタイプ)なので、小問2を早めに見切って大問4に時間を回すのは作戦として有効です。
- 計算:★★★(普通)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:小問2は解けなくてよい
大問4

講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、普通程度です。場合の数でおなじみ「C」を使った計算が続きます。閃きの必要性に関して、普通程度です。問1・問2で余事象を使い、問3で場合分けを使います。知識の必要性に関して、やや少ないです。基本レベルで解けます。
問1に関して、確率計算です。4つのサイコロの「積が25の倍数になる確率」を求めます。
ポイントは「余事象」です。
サイコロの積が25の倍数に「なる確率」を求めるのは大変ですが「ならない確率」を求めるのは簡単です。
- 4つのサイコロの積が25の倍数にならないのは
(ⅰ)5の目が1つ出た時
(ⅱ)5の目が1つも出ない時
の2通りである - (ⅰ)になる確率
₄C₁・1/6・(5/6)³
=500/6⁴…① - (ⅱ)になる確率
(5/6)⁴
=625/6⁴…② - よって、求める確率は
1-(①+②)
=19/144
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、確率計算です。4つのサイコロの「積が4の倍数になる確率」を答えます。
ポイントは「余事象」です。
サイコロの積が4の倍数に「なる確率」を求めるのは大変ですが「ならない確率」を求めるのは簡単です。
- 4つのサイコロの積が4の倍数にならないのは
(ⅰ)4つの目が奇数の時
(ⅱ)3つが奇数で残り1つが2か6の時
の2通りである - (ⅰ)になる確率
(3/6)⁴
=81/6⁴…③ - (ⅱ)になる確率
₄C₁・2/6・(3/6)³
=216/6⁴…④ - よって、求める確率は
1-(③+④)
=37/48
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、確率計算です。4つのサイコロの「積が100の倍数になる確率」を答えます。
ポイントは「5の個数で場合分け」することです。
様々なアプローチが考えられますが、できるだけ簡単に解きたいところです。
- 4つのサイコロの積が100の倍数になるには
25の倍数かつ4の倍数
となる必要がある - 5の目の個数で場合分けすると
(ⅰ)5が3つ出た時
(ⅱ)5が2つ出た時
の2通りである - (ⅰ)の時
残る1つの目は4となるため
求める確率は
₄C₁・(1/6)³・1/6
=4/6⁴…⑤ - (ⅱ)の時
残る2つのサイコロの積が4の倍数になるのは
(A)4が0個の時
(B)4が1個の時
(C)4が2個の時
に場合分けできる - (A)の時
残り2つのサイコロの出方は
(2,2)(2,6)(6,2)(6,6)
なので、確率は
4/6²…⑥ - (B)の時
残り1つのサイコロの出方は
4,5の目以外
なので、確率は
₂C₁・1/6・4/6
=8/6²…⑦ - (C)の時
確率は
1/6²…⑧ - ゆえに(ⅱ)になる確率は
₄C₂・(1/6)²・(⑥+⑦+⑧)
=78/6⁴…⑨ - よって、求める確率は
⑤+⑧
=41/648
(これが正解です)
合格者さんでも一定数が不正解になるレベルです。
正解できれば他者に差をつける1問です。
受験生としての解説
2020年の九大数学5問中、3番めの難易度です。
「場合の数・確率」は、時間をかけるほど正解に近づけます。合否の分かれ目となる「3番に簡単な大問」なので、時間を多めに使って高得点を目指したい1問です。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★(やや少ない)
- 総合:★★★(普通)
- 短評:時間をかけたい問題
大問5
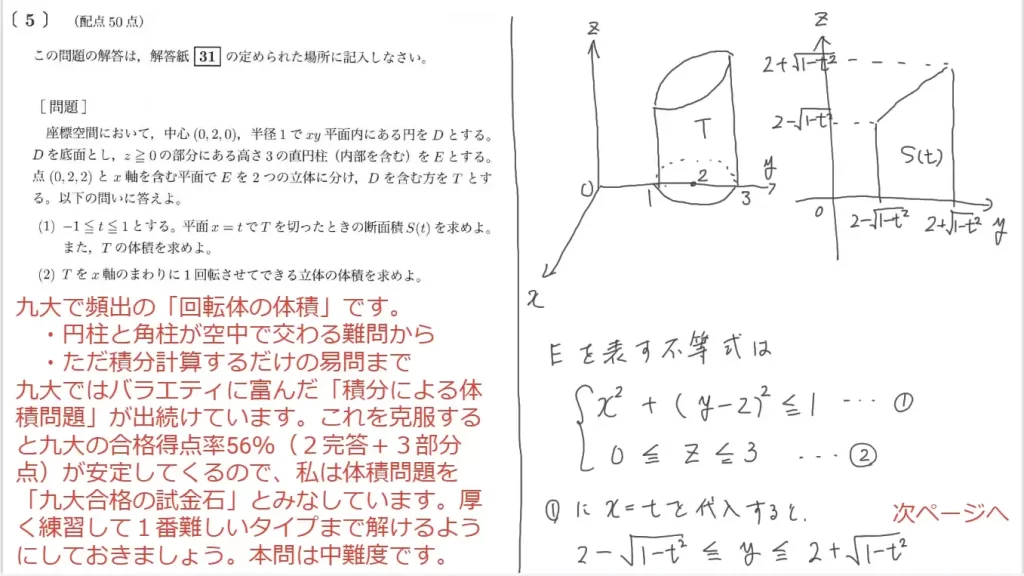
講師としての解説
「積分」による体積計算の出題です。
計算の量・難易度に関して、普通程度です。問1の断面積「y座標の値」がやや複雑ですが、九大ではよくある事です。閃きの必要性に関して、普通程度です。問2で回転体の体積を求める際に「切り口を回転させてから立体にする」と計算が楽になります。知識の必要性に関して、やや少なめです。積分による体積計算です。
問1に関して、面積計算です。円筒をx=tなる平面で切った切口(台形)の面積を答えます。
ポイントは「切口のy座標」です。
切口の形は台形なので、y座標さえわかれば断面積Sが求まります。Sをt(-1 → 1)で積分すればTの体積が求まるので、実質、y座標を求める問題です。
- 円Dの方程式は
x²+(y-2)²=1 - 平面x=tと円Dの交点のy座標は
t²+(y-2)²=1
∴ y=2±√(1-t²) - 点(0,2,2)とx軸を含む平面の方程式は
z=y
なので、切口の形状は
上底:2-√(1-t²)
下底:2+√(1-t²)
高さ:2√(1-t²)
の台形となる - よって
S(t)=4√(1-t²)
(これが正解です) - Tの体積をVとおくと
V=∫S(t)dt(積分範囲:-1→1)
=8∫√(1-t²)dt(積分範囲:0→1)
=8・π/4
=2π
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、積分による体積計算です。Tをx軸のまわりに1回転させてできる立体の体積を求めます。
ポイントは「回転体の切口が、切口の回転体」であることです。
これから求める「Tを回転させた立体の切口」は、問1で求めた台形を「原点中心に回転させたドーナツ形」に等しいです。
よって、問1で求めた台形を使います。
- 求める立体を
x=t(-1≦t≦1)
なる平面で切った切口は
問1の断面を原点中心に
1回転させたものに等しく
これをU(t)とおく - U(t)はドーナツ型であり
外側の半径:√2(2+√(1-t²))…①
内側の半径:2-√(1-t²)…②
より
U(t)=①²π-②²π
=π(5-t²+12√(1-t²)) - よって、求める立体の体積V’とすると
V’=∫U(t)dt(積分範囲:-1→1)
=28π/3+6π²
(これが正解です)
不合格者さんには厳しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
受験生としての解説
2020年の九大数学5問で、2番めに簡単な問題です。
小問1に関して、底円の方程式にx=tを代入するだけなので、全ての受験生さんが正解したい問題です。苦手とする学生さんは多いですが、九大の頻出分野ですし才能も必要ないので、ここは頑張って乗り越えてください。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★(やや少ない)
- 総合:★★★(普通)
- 短評:合否を分ける1問
九州大学の数学2019年・平成31年度
大問1

講師としての解説
「積分」からの出題です。
計算量・難易度に関して、やや簡単です。定積分の計算です。閃きの必要性に関して。ほぼ必要ありません。問題集のコピーの様な問題です。知識の必要性に関して、少ないです。部分積分と半角公式で正解できます。
誘導となる小問はありません。1手目に「カッコの2乗」を素直に開く事が少し難しいです。カッコ内は項が3つあるため、これを開くと項が6つに増えてしまいます。このカッコを素直に開くには、ある程度の計算力が必要です。本問を「難しい」と感じた学生さんは、積分の計算ドリルを1周する事をお勧めします。最後に極限がついてますが、これはオマケです。
- {sin(2nπt)-xt-y)²
=sin²(2nπt)+x²t²+y²–2xtsin(2nπt)+2xyt–2ysin(2πnt)…①
上記「黄色の項」は、普通の積分計算です。よって、赤と青を処理します。
- 半角公式より
sin²(2nπt)
={1-cos(4nπt)}/2…②
これで「赤の部分」も、普通の積分計算になりました。青の部分は「部分積分」で処理します。
- ∫tsin(2nπt)dt(積分区間:0→1)
=[t・{-cos(2nπt)/2nπ}]-∫{-cos(2nπt)/2nπ}dt
=-1/2nπ+[sin(2nπt)/(2nπ)²]¹₀
=-1/2nπ…③
①②③より、残りは平凡な積分計算だけとなりました。一気に片付けましょう。
- (与式)=2x/2nπ+[t/2-sin(4nπt)/8nπ+x²t³/3+y²t+xyt²-2y{-cos(2nπt)/2nπ}]¹₀
=x/nπ+1/2+x²/3+y²+xy
=(y+x/2)²+1/12(x+6/nπ)²-3/(nπ)²+1/2
上記は「x=-6/nπ」「y=-x/2」の時に、カッコ内が0になって「与式の最小値」を示します。
- In=-3/(nπ)²+1/2
- よって
lim In =1/2
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
受験生としての解説
2019年の九大数学5問で、1番簡単な問題です。
計算するだけなので、全ての受験生さんが正解したい問題です。九大数学は全5問から「2完答+3部分点」で非医歯薬系の合格得点率56%に届きます。本問を完答しておけば、残り「1完答+3部分点」で九大合格できます。
- 計算:★★(やや簡単)
- 閃き:★(ほぼ不要)
- 知識:★(計算)
- 総合:★(簡単)
- 短評:計算問題
大問2

講師としての解説
「恒等式」からの出題です。
計算量・難易度に関して、普通程度です。小問2において、係数比較の際にやや煩雑な計算があります。閃きの必要性に関して、普通程度です。小問1の「ともに2次以下」である事を示す部分で少し閃きが必要となります。知識の必要性に関して、普通程度です。恒等式の次数を求める際に、m次式・n次式と自分で設定する定石を知っておけば正解できます。
問1に関して、証明問題です。f(x)とg(x)がともに2次以下である事を示します。
ポイントは「f(x)をm次式・g(x)をn次式と仮定して計算を進めること」です。
- 左辺経由
- 右辺経由
2つの方法でf(x)とg(x)の次数を表してください。mかn一方だけでも3以上の場合は矛盾が発生します。背理法により「ともに2次以下」と証明・・・という流れです。
- f(x²)=(x²+2)g(x)+7…①
g(x³)=x⁴f(x)-3x²g(x)-6x²-2…② - f(x)≠0、g(x)≠0より
f(x)をm次式、g(x)をn次式とおく
(m・nは0以上の整数) - ①の両辺の次数より
2m=n+2…③ - ③において
mかnの一方が3以上の場合
もう一方も3以上となる…(A) - この時
②左辺の次数:3n=6(m-1)(∵③)
②右辺の次数:m+4またはn+2=2m(∵③) - ここで②において
(左辺の次数)-(右辺の次数)とすると
6(m-1)-(m+4)=5(m-2)>0(∵m≧3)
または
6(m-1)-2m=4(m-3/2)>0(∵m≧3)
となり
いずれの場合も矛盾する…(B) - よって(A)(B)より
m,nはともに2以下であるため
題意を証明できた(証明終了)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問2に関して、f(x)とg(x)を求める問題です。
ポイントは
- f(x)=ax²+bx+c
- g(x)=dx²+ex+h
とおいて考えることです。
問1の結果より「f(x)とg(x)は2次以下」なので、この事実を利用します。後は係数比較で正解・・・という流れです。
- ②より
g(0)=-2
ゆえに①より
f(0)=3
となる - (1)の結果より
f(x)とg(x)はともに2次以下なので
f(x)=ax²+bx+3…④
g(x)=cx²+dx-2…⑤
とおける - ①を④⑤を使って表すと
ax⁴+bx²+3=(x²+2)(cx²+dx-2)+7
=cx⁴+dx³+(2c-2)x²+2dx+3 - 両辺の係数を比較して
a=c
d=0
b=2c-2
より
f(x)=cx²+(2c-2)x+3…⑥
g(x)=cx²-2…⑦ - ②を⑥⑦を使って表すと
cx⁶-2=x⁴{cx²+(2c-2)x+3}-3x²(cx²-2)-6x²-2
=cx⁶+(2c-2)x⁵-(3c-3)x⁴-2 - 両辺の係数を比較して
c=1 - よって
f(x)=x²+3(これが正解です)
g(x)=x²-2(これが正解です)
係数比較するだけなので、不合格者さんでも正解してきます。
問1が不正解でも問2を正解できる事は重要です。
よって、全ての受験生さんが正解したい問題です。
受験生としての解説
2019年の九大数学5問で、2番めに簡単な問題です。
小問1に関して、恒等式を「m次・n次」と設定して解く方法は問題集に必ず載っているので、正解しておきたいところです。
- 計算:★★★(普通)
- 閃き:★★★(やや必要、証明問題)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:小問1を解けずとも小問2は解ける
高校偏差値60の高校で落ちこぼれ「1番簡単な国立大学を目指せない」と苦しんでいる学生さんでも取れるようになっています。学区1位の高校で落ちこぼれ「熊本大学を目指せない」と苦しんでいる学生さんなら、少し余裕を持ってこれ以上のレベルになっています。
大問3

講師としての解説
「複素数平面」と「確率」からの出題です。
計算量・難易度に関して、普通程度です。小問の条件に合わせてサイコロの出目を書き出します。閃きの必要性に関して、普通程度です。
- 方程式の解の条件
- 複素数平面
- 場合の数・確率
の3分野を行き来するため、やや思考を要します(普通は2分野)知識の必要性に関して、普通程度です。上記3分野の基本知識で正解できます。
問1に関して、確率計算です。与式の「2つの解」が複素数平面上で一致する確率を答えます。与式が「重解を持つ確率」なので「判別式=0」の式を立て、それを満たすサイコロの出目(a,b,c)を書き出せば正解です。問2に関して、確率計算です。与式の「2つの解」が単位円の周上にある確率を答えます。単位円の周上において
- 1と-1だけは実数(判別式≧0)
- 他の値は虚数(判別式<0)
なので、場合分けして考えます。それぞれの判別式を満たすサイコロの出目(a,b,c)を書き出せば正解です。問3に関して、確率計算です。与式の「2つの解z1・z2」と原点Oを結ぶ直線が60°で交わる確率を答えます。ポイントは、2つの解が必ず「共役の関係」になる事です。これにより2つの解と原点Oを結ぶ直線が60°で交わるのは、解の偏角が
- 120°
- 150°
の2パターンしか無いと解ります。よって、ここで解答範囲が小さく絞れたため、サイコロの出目(a,b,c)を書き出せば正解となります。
受験生としての解説
2019年の九大数学5問で、2番めに難しい問題です。
小問1に関して、判別式=0を満たすサイコロの出目を書き出すだけなので、全ての受験生さんが正解したい問題です。小問2に関して、基本的な考え方は小問1と同じですが「1と-1だけは実数で残りは虚数」と場合分けする部分が少し難しいため、合否を分ける1問です。小問3に関して、「医学科限定」と言うほど難しくありませんが、非医歯薬系の合格レベルは超えています。よって、正解できれば他者に差をつけられる1問です。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:小問2まで正解したい
高校偏差値60の高校で落ちこぼれ「1番簡単な国立大学を目指せない」と苦しんでいる学生さんでも取れるようになっています。学区1位の高校で落ちこぼれ「熊本大学を目指せない」と苦しんでいる学生さんなら、少し余裕を持ってこれ以上のレベルになっています。
大問4

講師としての解説
「数列」からの出題です。
計算量・難易度に関して、やや簡単です。漸化式の計算です。閃きの必要性に関して、普通程度です。出題のシチュエーションに合わせ、自分で漸化式を立てます。知識の必要性に関して、やや少ないです。「垂線を下ろす」というヒントがあるため「直交条件」や「三角関数」など、直角に関する知識を使うことになります。
誘導となる小問はありません。Pnのx座標をx=tと置き、直交条件を使って線分OBに下ろした「垂線の足の座標」を求める。その座標から、線分OAに垂線を下ろした足の座標を求める(これはy=0でx=そのまま)その座標から、線分ABに下ろした垂線の足の座標がPn+1なので漸化式が立ち、解けば正解できます。不格好な解き方ですが、才能が無くても思いつくし安全です。
- 直線ABの方程式は
y=-√3x+2√3…①
直線OBの方程式は
y=√3x…② - 点Pnのx座標をtとおくと
Pn(t,-√3t+2√3)
となる - 点Pnを通り直線OBと直交する
直線の方程式は
y=-x/√3+(-√3+1/√3)+2√3…③
であり、これは直線PnQnを表す - ②と③の交点が点Qnなので
点Qnのx座標=-t/2+3/2
ゆえに点Rnの座標は
Rn(-t/2+3/2,0) - 点Rnを通り直線ABと直交する
直線の方程式は
y=x/√3+1/√3(t/2-3/2)…④
であり、これは直線RnPn+1を表す - ④と①の交点が点Pn+1なので
点Pn+1のx座標=-t/8+15/8 - ここで
点Pnのx座標をtn
点Pn+1のx座標をtn+1
と表すと
tn+1=-tn/8+15/8…⑤
【ここは解答用紙に書かないメモ】
- ⑤の特性方程式は
α=-α/8+15/8…⑥
∴ α=5/3 - ⑤-⑥より
tn+1-α=-1/8(tn-α)
- ∴ tn+1-5/3=-1/8(tn-5/3)
∴ tn-5/3=(t1-5/3)(-1/8)^n-1
∴ tn=(t1-5/3)(-1/8)^n-1+5/3 - ここで
1≦t1≦2
なので
(n→∞の時)lim tn=5/3…⑦ - ⑦を①に代入して
y=√3/3…⑧ - よって、点Pnが限りなく近づく点は
(x,y)=(⑦,⑧)=(5/3,√3/3)
(これが正解です)
模範解答に比べ冗長ですが
この解き方なら才能が無い人でも試験中に思い付けます。
また、中学生でも正解できます。
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
受験生としての解説
2019年の九大数学5問、3番めの難易度です。
難しそうな大問3・大問5に比べ、本問は「正三角形」と「直交条件」が与えられているため、頑張れば解けそうな気がします(実際解けます)よって、大問3~5の中では本問で完答を目指すのが楽そうです。簡単な大問1・大問2を完答できた状態で本問も完答できれば、それだけで数学の得点率約60%となり非医歯薬系の合格ライン56%を超えてきます。
- 計算:★★(やや簡単)
- 閃き:★★★(普通)
- 知識:★★(やや簡単)
- 総合:★★★(普通)
- 短評:不格好でも安全・確実に
大問5

講師としての解説
「複素数平面」からの出題です。
計算量・難易度に関して、やや難しいです。複素数の煩雑な計算が続きます。閃きの必要性に関して、やや強く必要です。zが純虚数と判明したところでkiと置き換えたり、置き換えたkを軌跡のために三角関数へ再度置き換えたり、難しい条件(ウ)を処理したりと、試験中に考える要素が多いです。知識の必要性に関して、普通程度です。複素数平面の基本知識を一通り使えれば正解できます。
- 以下、ある複素数pと共役の関係にあるものを
p*と表す(「*」は「 ̄」の代わり) - 与式
w=(az+b)/(cz+1)…①
において
z=i
z=-i
とすると、条件(ア)より
i=(ai+b)/(ci+1)
-i=(-ai+b)/(-ci+1)
ゆえに
-c+i=ai+b…②
-c-i=-ai+b…③
となる - ②+③より
b=-c
②-③より
a=1
これらを①に代入すると
w=(z-c)/(cz+1)…④
となる - ④と条件(イ)より
|w|=|(z-c)/(cz+1)|=1
∴ |(z-c)|=|(cz+1)|…⑤ - 題意より、zは純虚数なので
実数kを用いて
z=ki
と表すと⑤は
|(ki-c)|=|(kci+1)|
∴ |(ki-c)|²=|(kci+1)|²
∴ (ki-c)(-ki-c*)=(kci+1)(-kc*i+1)
∴ k²+ki(c-c*)+|c|²=k²|c|²+ki(c-c*)+1
∴ k²(|c|²-1)-|c|²+1=0…⑥ - 題意より
⑥は任意のkで成立するので
|c|²=1
∴ cc*=1…⑦ - 今、条件(ウ)と④より
(z-c)/(cz+1)=-1…⑧
という式が成り立ってはならないため
⑧を成立させてしまうcの条件について考える - ⑧より
(c+1)z=c-1…⑧’
において
c=-1ではなりたたない - c≠-1の時
⑧’より
z=(c-1)/(c+1)
=(1-1/c)/(1+1/c)
=(1-c*)/(1+c*)(∵⑦)
=-(c*-1)/(c*+1)
=-z*
となるが、これはすなわち
z=-z*なる純虚数zにおいて
⑧が成り立つ事を意味しており不適である
ゆえに
c=-1…⑨
となる
これで与式からa,b,cを消去できました。正解まであと少しです。
- ここでz=kiと⑨を④に代入すると
w=(ki+1)/(-ki+1)
=(1+ki)²/(1-ki)(1+ki)
=(1-k²)/(1+k²)+2ki/(1+k²)
作図のために実部と虚部に分けました。実部がx座標、虚部がy座標になるため、これで作図できます。
- 実数x,yを用いて
z=x+yi
と表すと
x=(1-k²)/(1+k²)
y=2k/(1+k²) - kは任意の実数なので
k=tanθ(-π/2<θ<π/2)
と表すことができ
これにより
x=(1-tan²θ)/(1+tan²θ)
=(cos²θ-sin²θ)/(cos²θ+sin²θ)
=cos2θ
y=2tanθ/(1+tan²θ)
=2sinθcosθ/(cos²θ+sin²θ)
=sin2θ - よって与式は
w=cos2θ+isin2θ(-π/2<θ<π/2)
となり、作図は
「単位円から点(-1,0)を除いたもの」となる
(これが正解です)
合格者さんでも難しいレベルです。
しかし「医学科の合否を分ける1問」と言うほど難問ではありません。
よって、正解できれば他者に差をつける1問です。
受験生としての解説
2019年の九大数学5問で、1番難しい問題です。
(ア)に関して、問題文の通りに立式するだけで「wの式」からa・bを消すことができるので、全ての受験生さんが記述しておきたい部分です。
(イ)に関して、文章から「絶対値=1」を使う事は解りやすいので、全ての受験生さんが記述しておきたい部分です。移項して、絶対値を消すために両辺2乗するところも定番の流れです。
(ウ)に関して、「属さない」という条件から「cの値」を求める部分が難しいので、ここで行き詰まる事は仕方ないです(医学科・臨床科は正解必須です)
2019年は大問1・大問4が正解しやすく、大問2・大問3もそれほど難しくないので、簡単な順に優先してください。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:条件(ウ)が難しい
九州大学の数学2018年・平成30年度
大問1

講師としての解説
「空間ベクトル」と「双曲線」からの出題です。
計算量・難易度に関して、普通程度です。軌跡の計算で、出てくる式は比較的シンプルです。閃きの必要性に関して、やや少なめです。基本的に「問題集のコピーの様な問題」なので閃きは不要ですが、本問のシチュエーションに合わせる部分で頭を使います。知識の必要性に関して、普通程度です。軌跡問題の知識が必要です。
誘導となる小問はありません。x座標がdで定まった軌跡問題なので、ゴールは「yとzの式」になります。よって「x・y・z」の式を2本連立し「xを消去」する事が基本的な流れです。求める交点は直線AP上にあるため、実数kを使って「AP=kAQ」と表すことができます。よって「文字k」が1つ増えるので「x・y・z・k」の式を3本連立し「xとkを消去」すればよいと解ります。3本の式とは
- x座標に関する式
- y座標に関する式
- z座標に関する式
なので、すぐ立式できます。これを解けば正解・・・という流れです。
以下、ベクトルの「→」の代わりに「*」を使います。
<例>
「→X」→「X*」と表記
- 点Pの座標を(x,y,0)とおくと
x²-y²=1…①
かつ
x≧1…②
となる - また
直線APと平面x=dの交点を
Q(d,Y,Z)とおくと
3点A・P・Qは同一直線上にあるため
ある実数kを用いて
AP*=kAQ*…③
と書ける - ③より
(x,y,-1)=k(d,Y,Z-1)
ゆえに
x=kd…④
y=kY…⑤
-1=k(Z-1)…⑥ - 今、⑥において
Z=1は成り立たないので
Z-1≠0
ゆえに⑥より
k=1/(1-Z)…⑥’ - ⑥’を④⑤へ代入して
x=d/(1-Z)…④’
y=Y/(1-Z)…⑤’
このx・yは元々点P(x,y,0)から来ているので、①②へ代入できます。ここが本問のポイントです。
- ④’⑤’を①②へ代入して
{d/(1-Z)}²-{Y/(1-Z)}²=1…⑦
かつ
d/(1-Z)≧1…⑧ - ⑦より
Y²+(Z-1)²=d²…⑦’
⑧より
1-d≦Z<1…⑧’ - よって⑦’⑧’より
求める点Qの奇跡は
平面x=d上の点(d,0,1)を中心とする
半径dの円のz<1の部分
となる
(これが正解です)
不合格者さんの中に一定数の不正解者が出るレベルです。
合格者さんは正解してきます。
よって、合否を分ける1問より少し簡単な問題です。
受験生としての解説
2018年の九大数学で、2番めに簡単な問題です。
九大数学は大問5つから「2完答+3部分点」で非医歯薬系の合格点(得点率56%)を作れます。2018年は大問1・大問2が簡単だったので、本問は完答しておきたいところです。「難しい、難しい」と言われる九大数学ですが、合格点を取るだけなら大問1・大問2レベルで可能です。
- 計算:★★★(普通)
- 閃き:★★(やや少ない、問題集のコピーの様な問題)
- 知識:★★★(普通)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問2

講師としての解説
「図形と方程式」と「積分」からの出題です。
計算量・難易度に関して、普通程度です。主に軌跡の計算で、使われる数値はシンプルです。閃きの必要性に関して、やや少なめです。問題のシチュエーションに合わせて作図し、できるだけ簡単に面積を求めます。知識の必要性に関して、やや少なめです。「軌跡」と「積分による面積」の知識を使います。
以下、ベクトルの「→」の代わりに「*」で表します。
<例>「→OP」→「OP*」
問1に関して、面積計算です。線分PRが通過してできる図形の面積を答えます。
ポイントは「三角関数」です。
原点中心の円なので、各点は三角関数を使って容易に表せます。点Rのx座標・y座標を「sin²θ+cos²θ=1」に代入すると「点Rの軌跡」が求まります。ここで求める面積が「円の1/4+楕円の1/4」と解るので、積分せずとも図形的に正解できる・・・という流れです。
- 条件より
P(-3cosθ,3sinθ)
Q(3cosθ,3sinθ)
0≦θ<π/2…①
とおく - 点Rは線分PQの内分点なので
OR*=(OP*+2OQ*)/3
=(cosθ,3sinθ) - ここでR(x,y)とおくと
cosθ=x
sinθ=y/3 - cos²θ+sin²θ=1
より
x²+y²/9=1
となり、これは①より
楕円の第1象限部分を表している - よって
S=3・3・π・1/4+1・3・π・1/4
=3π
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、点Pを(-3,0)に固定した時の、線分PRが通過してできる図形の面積を答えます。
ポイントは「三角関数」です。
問1と同じ流れで正解できます。今回は「半円」なので、やはり積分せずとも面積計算できます。
- 条件より
Q(3cosθ,3sinθ)
0≦θ<π…②
とおく - 点Rは線分PQの内分点なので
OR*=(OP*+2OQ*)/3
=(-1+2cosθ,2sinθ) - ここで点R(x,y)とおくと
x=-1+2cosθ
y=2sinθ - cos²θ+sin²θ=1
より
(x+1)²/4+y²/4=1
∴ (x+1)²+y²=4…③
となり、これは②より
半径2の円の上半分を表している - よって
T=2・2・π・1/2
=2π
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、図形U(図形Sから図形Tを除いたもの)をy軸まわりに1回転させてできる「回転体の体積」を答えます。
ポイントは「回転させてから引く」ことです。
一気に計算すると大変なので、なるべく簡単にしましょう。問1で求めた「楕円の回転体」から、問2で求めた「半円の回転体」を引き算すると正解・・・という流れです。
- 図形Sの第1象限部分を
y軸まわりに回転した体積をV₁とおくと
V₁=∫x²πdy(積分区間:0→3)
=∫(1-y²/9)πdy
=π[y-y³/27]
=2π - ③より
x=-1±√(4-y²)
であり
図形Tの第1象限部分を
y軸まわりに回転した体積をV₂とおくと
V₂=∫x²πdy(積分区間:0→√3)
=∫{-1+√(4-y²)}²πdy
=(3√3-4π/3)π - よって、求める体積は
V₁-V₂=(2-3√3+4π/3)π
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
受験生としての解説
2018年の九大数学5問で、1番簡単な問題です。
小問1・小問2が誘導で、小問3が本番の勝負という構成です。しかし、小問3も九大としては簡単な部類なので完答したい問題です。九大数学は大問5つから「2完答+3部分点」で合格点(得点率56%)を作れます。2018年は簡単な大問1・大問2を完答しておけば、難しい大問4・大問5を解けずとも合格できます。
- 計算:★★★(普通)
- 閃き:★★(やや少ない)
- 知識:★★(やや少ない)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問3

講師としての解説
「数列」と「場合の数・確率」からの出題です。
計算量・難易度に関して、普通程度です。4パターンの確率について、漸化式を4連立するため煩雑な計算が続きます。しかし、難しくはありません。閃きの必要性に関して、普通程度です。やや複雑な問題シチュエーションの理解、それを漸化式で表す事など、普通程度の閃きが必要です。知識の必要性に関して、やや少ないです。漸化式の一般項を求める手順を知っていれば解けます。
誘導となる小問はありません。問題文で「p・q・r・s」が提示されているので、4パターンの確率に関する漸化式を解けばよいと解ります。n=1の時の確率が各々1/4と明らかなので、n回目からn+1回目への変化を1つずつ丁寧に探っていけば正解・・・という流れです。
- 条件より
p₁=q₁=r₁=s₁=1/4…①
pn+qn+rn+sn=1…② - n回目終了時の状態(pn~sn)と
n+1回目のカードによる
積を4で割った余りは下表の様になる
| n+1回目の カード→ | 1 | 2 | 3 | 4 |
| pn | 余り 0 | 0 | 0 | 0 |
| qn | 1 | 2 | 3 | 0 |
| rn | 2 | 0 | 2 | 0 |
| sn | 3 | 2 | 1 | 0 |
- ゆえに
pn+1=pn+1/4・qn+1/2・rn+1/4・sn…③
qn+1=1/4・qn+1/4・sn…④
rn+1=1/4・qn+1/2・rn+1/4・sn…⑤
sn+1=1/4・qn+1/4・sn…⑥ - ④⑥より
qn+1 = sn+1
また、①より
q₁=s₁
なので
qn=sn…⑦ - ゆえに④⑦より
qn+1 = 1/2・qn
∴ qn=q₁(1/2)^n-1
=(1/2)^n+1…③’
(これが正解です) - qn=snより
sn=(1/2)^n+1…⑥’
(これが正解です) - ③’⑥’を⑤に代入して
rn+1 =1/2・rn +(1/2)^n+2
(α=1/2α+(1/2)^n+2)
両辺に2^n+1をかけて
2^n+1・rn+1=2^n・rn+1/2 - ゆえに
{2^n・rn}は
初項1/2、公差1/2の等差数列なので
2^n・rn=1/2+(n-1)・1/2
=n/2
∴ rn=n(1/2)^n+1…⑤’
(これが正解です) - ②と③’⑤’⑥’より
pn=1-(③’+⑤’+⑥’)
=1-(n+2)(1/2)^n+1
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
受験生としての解説
2018年の九大数学5問で、3番めの難易度です。
誘導となる小問が無いため、ポイントを自分で判断すると
- 「p1=q1=r1=s1=1/4」に気づけるか
- p・q・r・sの「n回目→n+1回目」の漸化式を立てられるか
- 4つの漸化式を連立して正解を導けるか
となります。
やっかいなのは上記「ポイント2」が決して簡単ではなく、同時に「解答の序盤」に来ることです。よって、ポイント2ができない場合は白紙解答に近い状態で提出することになり、大量失点となります。
よって、対策としては
- n回目→n+1回目の漸化式を立てる練習をしておく
- 「p1=q1=r1=s1=1/4」だけは書いて白紙解答を避ける
となります。
2018年の九大数学は大問4・大問5が難しく、大問1・大問2が簡単なので、本問が「合否を分ける1問」となります。また、九大数学の「場合の数・確率」は時間をかけて思考・手作業を重ねるほど正解に近づける(部分点を拾える)分野です。よって、本問に多く時間を回したいところです。
そのために大切な事は
- 大問1・2を素早く解くこと
- 大問4・5が難しいと見抜き、適切に見切ること
です。
どうしても本問に取り付けない場合は、誘導問題で部分点を狙いやすい大問4に力を入れると良いです。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★(やや少ない)
- 総合:★★★(普通)
- 短評:完答したい
大問4

講師としての解説
「整数」からの出題です。
計算量・難易度に関して、やや難しいです。問2・背理法からの証明、問3・有理数の仮定からの処理で計算量が多いです。閃きの必要性に関して、やや強く必要です。
- 問1の「3の倍数ではない」から「a≡±1」とする発想
- 問2で条件を満たすxが存在した場合に「x<0」となる事
- 問3のa・bを求める時の式の処理
など、その場の閃きを要求されます。知識の必要性に関して、普通程度です。合同式の扱い方、背理法、有理数の定義、いずれも普通程度の知識です。
問1に関して、f(1)とf(2)を3で割った余りを求める問題です。
ポイントは、3で割った余りを「1・2ではなく±1と表すこと」です。
これにより、余りが「+1」でも「-1」でも余りの2乗が「1」となります。よって、計算を簡略化できます。
- 条件より、a,bは3の倍数ではないため
a≡±1(mod3)
b≡±1(mod3)
と書ける - 今
f(1)=a²+2b²+3
f(2)=4a²+4b²+17
なので
3を法とする合同式を立てると
f(1)≡1+2+3≡0(これが正解です)
f(2)≡4+4+17≡1(これが正解です)
不合格者さんでも正解してくるレベルです。
よって、全ての受験生さんが正解したい問題です。
問2に関して、証明問題です。f(x)=0を満たす「整数xが存在しない事を証明」します。
ポイントは「背理法」です。
「存在しない事を証明せよ」なので「存在する」と仮定し、その矛盾を突けば正解・・・という流れです。
- f(x)=2x³+a²x²+2bx²+1…①
f(x)=0を満たす整数x=αが存在すると仮定する - (ⅰ)α≧0の時
①の左辺≧1
となるため不適 - (ⅱ)α<0の時
2α³+a²α²+2b²α+1=0
∴ -α(2α²+a²α+2b)=1…② - ここで、2α²+a²α+2bは整数なので
-αは1の約数となるが
(ⅱ)の条件α<0より
α=-1となる - よって
f(-1)=a²-2b²-1=0…③
となるが
a²-2b²-1を
3を法とする合同式で表すと
a²-2b²-1
≡1-2-1
≡1
となるため③に矛盾する - よって
f(x)=0を満たす整数xは存在しない
(証明終了)
「x≧0の時、f(x)≧1」でxの条件をバッサリ消せる事に気付く部分がやや難しいです。
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問3に関して、f(x)=0を満たす有理数の組み合わせを求めます。
ポイントは、整数p・qを用いて「x=p/q」とおくことです。
【有理数の定義】
分母・分子ともに整数の分数(分母≠0)として表すことができる実数
有理数を扱う時の、定番の解き方となります。
- f(x)=0を満たす有理数xが存在する場合
互いに素な整数p・q(q≧2)を用いて
x=p/q
と書ける - f(p/q)
=2(p/q)³+a²(p/q)²+2b²・p/q+1
=0
∴ 2p³=-q(a²p²+2b²pq+q²)…④ - 今、a²p²+2b²pq+q²は整数であり
p,qは互いに素な整数(q≧2)なので
q=2
となる
一気に「q=2」が確定しました。ここが本問のポイントです。1ヶ所でも確定してしまえば、後は同じ流れで正解にたどり着けます。
- ④においてq=2とすると
2p³=-2(a²p²+4b²p+4)
p(p²+a²p+4b²)=-4…⑤ - p²+a²p+4b²は整数なので
pは4の約数となり
q=2と互いに素であることをふまえると
p=1または-1
となる - (A)p=1の時
⑤より
1+a²+4b²=-4
となるが
(左辺)≧1より、右辺に矛盾する - (B)p=-1の時
⑤より
-(1-a²+4b²)=-4
∴ a²-4b²
=(a+2b)(a-2b)
=-3 - よって、これを満たすa,bの組み合わせは
(a,b)=(1,1)(1,-1)(-1,1)(-1,-1)
(これが正解です)
であり、a,bが3の倍数でない条件にも適合する
定番そのままの解き方なので、正解したいところではあります。
しかし、不合格者さんには難しいでしょう。
合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
受験生として
2018年の九大数学5問で、2番めに難しい大問です。
問1に関して、合格者さんは正解するが不合格者さんには厳しいレベルなので、合否を分ける1問です。九大数学では小問(1)において
- 小問1だけでも正解して部分点をかせぐか
- 大問丸ごと0点になるか
で、合否が分かれる事がよくあります。「整数」は難しい分野ですが、定石を身に着け小問1だけでも解ける状態を作ることは、非医歯薬系の合格に直結します。また、3で割った余りは「1か2」の2つしかないので、上手な解き方を思いつかなくても、時間をかければ正解できます。
問2に関して、背理法を使った後で「aが存在するとしたら-1しかありえない(+1はダメ)」と導く部分がやや難しいですが、これも基本の定石で「ジャスト合格ライン」というレベルなので、合否を分ける1問です。非医歯薬系の受験生さんでもここまでは部分点を拾いたいところです。
問3に関して、「有理数=p/q」と置いて解き進める事も定石ですが、なかなか整数問題の定石まで完璧に身につける事も難しいので、正解できれば他者に差をつけられる1問と言えます。
「2番めに難しい大問」とはいえ、最後の小問3まで定石なので、非医歯薬系の志望者さんでも完答を狙えます。ただ、整数問題をガチガチに固めるよりは、英語・物理・化学の簡単な部分で他にやるべき事があるでしょう。「5教科トータルの作戦」が九大受験のコツです。
- 比較的簡単な大問1・大問2を完答
- 大問3から部分点
- 大問4を完答
とできた場合は、非医歯薬系の合格得点率56%を大きく超え、英語・化学・物理の失点を補うことができます。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:問2まで解きたい
大問5

講師としての解説
「複素数平面」からの出題です。
計算量・難易度に関して、やや難しいです。複雑な計算を要求されます。閃きの必要性に関して、やや強く必要です。与式は複雑ですが、ある1点(下記)に気付くと正解まで一気に流れます。知識の必要性に関して、普通程度です。特別な知識は不要ですが、複素数の基本式や実数・虚数に関して正確で柔軟な運用を求められます。
ポイントは「|z|²と|α|²が実数」であることです。
与式は複雑ですが、|z|²と|α|²が実数なら、複雑な部分を全部まとめて「=k」と置き換えることができます。
- 以下、ある複素数pと共役の関係にあるものを
「*」を使ってp*と表す( ̄の代わり) - 与式
α(|z|²+2)+i(2|α|²+1)z*=0…①
において
2|α|²+1≠0
より
z*=-α(|z|²+2)/i(2|α|²+1)
=(|z|²+2)/(2|α|²+1)・iα…①’ - 今、(|z|²+2)/(2|α|²+1)は実数なので
k=(|z|²+2)/(2|α|²+1)
とおくと、①’は
z*=kiα…②
となり
z=-kiα*…③
|z|²=zz*=k²|α|²…④
となる - ②③④を①に代入すると
α(k²|α|²+2)+i(2|α|²+1)kiα=0
∴ α{k²|α|²-(2|α|²+1)k+2}=0
∴ α(|α|²k-1)(k-2)=0…⑤ - 題意である「①をみたす複素数z」とは
⑤を満たす複素数zのことなので
(ⅰ)α=0
(ⅱ)k=1/|α|²
(ⅲ)k=2
におけるzのことを指す - (ⅰ)の時
③より
z=0 - (ⅱ)の時
③より
z=-1/|α|²・iα*
=-1/αα*・iα*
=-i/α - (ⅲ)の時
③より
z=-2iα* - (ⅰ)~(ⅲ)より
求める複素数zは
α=0の時
z=0(これが正解です)
α≠0の時
z=-i/α , -2iα*(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
受験生としての解説
2018年の九大数学5問の中で、1番難しい問題です。
- 複雑な実数部分を固めて「=k」と置くこと
- 複素数を左辺・右辺に分けて係数比較する事
は定石ではありますが、全てを完璧に仕上げる事は不可能なので(英語・物理・化学の簡単な事の方が得点効率が良いので)非医歯薬系の合格ラインより少し上、正解できれば他者に差をつけられる1問となります。
大問1・2を完答し、大問3・4から部分点を回収して合格得点率56%を確保できたなら、本問から高得点を取る必要はありません。しかし、本問も突出して難しくはないので、部分点を回収したいところです。大問3・大問4が頭打ちになった場合は、あえて大問5に注力するのも有効です。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:気づけば一気
九州大学の数学2017年・平成29年度
大問1

講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、やや簡単です。基本的な積分計算だけで量も多くありません。閃きの必要性に関して、やや少なめです。問題集のコピーの様な問題です。知識の必要性に関して、やや少なめです。直交条件や積分による面積計算の知識で正解できます。
問1に関して、曲線C₁とC₂が原点以外にも交点を持つための「aの条件」を答えます。
「交点を持つ条件」なので2式をイコールでつなぎます。「2倍角の公式」と「tanの公式」でsin・cosだけの式にし、sinxを消去してcosxの範囲を確認すれば正解・・・という流れです。
- y=atanx…①
y=sin2x…②
0<x<π/2…③ - ①②からyを消去して
atanx=sin2x…④ - ④を満たすx(0<x<π/2)が存在するような
aの条件を求めればよいので
④より
asinx/cosx=2sinxcosx
③より、sinx>0なので
a=cos²x - ③より
0<cosx<1
∴ 0<2cos²x<2
∴ 0<α<2
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、曲線C₁とC₂の接線が直交する時の「aとcos2p」の値を求めます。
ポイントは「接線が直交」という条件です。
直行条件の式(傾き×傾き=-1)を使います。その式を解けば「aとcos2p」が求まって正解・・・という流れです。
- ①②をxで微分すると
y’=a/cos²x…⑤
y’=2cos2x…⑥ - x=pは(1)の条件を満たすので
⑤⑥と直交条件より
a/cos²p・2cos2p=-1
∴ 2a(2cos²p-1)=-cos²p…⑦ - (1)より
a=2cos²pなので
⑦より
2a(a-1)=-a/2
∴ a=3/4(∵ 0<a<2)
(これが正解です) - また
cos2p=2cos²p-1
=a-1
=-1/4
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、積分による面積計算です。
ポイントは「tanxの積分」です。
【tanxの積分】
∫tanx dx
=∫sinx/cosx・dx
=∫-(cosx)’/cosx・dx
=-log|cosx|+C
(Cは積分定数)
上側の曲線C₂から下側のC₁を引き、積分すると正解・・・という流れです。
- 求める面積をSとおくと
S=∫(sin2x-3/4・tanx)dx(積分区間:0→p)
=[-1/2・cos2x+3/4・log(cosx)]
=-1/2・cos2p+3/4・log(cosp)+1/2
=5/8+3/8・log(3/8)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
受験生としての解説
2017年の九大数学で、2番めに簡単な問題です。
最頻出の「微分積分」かつ難易度は基本レベルということで、完答しておきたい1問です。九大数学は5つの大問から「2完答+3部分点」で非医歯薬系の合格ライン(得点率56%)に届きます。大問1・大問2の様な簡単な問題を正解しておけば、大問3・大問5の様な問題から部分点を取るだけで九大合格できます。
- 計算:★★(やや簡単)
- 閃き:★(簡単、問題集のコピーの様な問題)
- 知識:★★(やや簡単、tanの積分)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問2

講師としての解説
「空間ベクトル」からの出題です。
計算量・難易度に関して、簡単です。やや複雑な分数の式が出ますが、最終的に約分でバッサリ消えます。閃きの必要性に関して、ほぼ不要です。点Gが内分点になるため、自分で「実数t」を設定して解きますが、これは共通テストの頻出パターンです。知識の必要性に関して、簡単です。「内分点の式」と「内積」が必要ですが、これは基本レベルです。
問1に関して、点Aから線分CDに下ろした垂線の足「点Gの座標」を答えます。
ポイントは「内積=0」です。
点Gは線分CDの内分点なので「実数t」を使ってOCベクトルとODベクトルで表せます。点Gが判ればAGベクトルが判り、これがCDベクトルと直交するので「内積=0」から正解・・・という流れです。
以下、ベクトルの「→」の代わりに「*」を使います。
<例>
「→X」→「X*」と表記
- 点Gは線分CDの内分点なので
0≦t≦1なる実数tを用いて
OG*=(1-t)OC*+tOD*…①
と表すことができる - 今
AG*=OG*-OA*
=(at-a,bt,1)
であり
AG*⊥CDなので
AG*・CD*=0
∴ (at-a)・a+bt・b=0
∴ t=a²/(a²+b²)…② - ①②より、点Gの座標は
(a³/(a²+b²),a²b/(a²+b²),1)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、cosθの値を求めます。
ポイントは「内積」です。
ベクトルで「なす角θ」と言えば内積です。
- 問1と同様の方法で点Hを求め
- 要素のかけ算で内積を出し
- 三平方の定理でベクトルの大きさを求め
上記3つを内積の式に代入すればcosθが求まり正解・・・という流れです。
- (1)と同様にすると、点Hの座標は
(ab²/(a²+b²),b³/(a²+b²),1)
である - よって
AG*=(-ab²/(a²+b²),a²b/(a²+b²),1)
BH*=(ab²/(a²+b²),-a²b/(a²+b²),1) - ここで
|AG*|=√{(a²b²+a²+b²)/(a²+b²)}
|BH*|=√{(a²b²+a²+b²)/(a²+b²)}
であり
AG*・BH*
=(-a²b²+a²+b²)/(a²+b²) - cosθ=AG*・BH*/|AG*||BH*|
=(-a²b²+a²+b²)/(a²b²+a²+b²)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
受験生としての解説
2017年の九大数学5問で、1番簡単な問題です。
共通テストの頻出解法だけで正解できます。ぜひ完答したい1問です。
- 計算:★(簡単)
- 閃き:★(簡単)
- 知識:★(簡単)
- 総合:★(簡単)
- 短評:完答したい1問
大問3

講師としての解説
「数列」と「整数」からの出題です。
計算量・難易度に関して、やや難しいです。数列に関する煩雑な計算が続きます。閃きの必要性に関して、やや強めに必要です。特に問3は思考力を要求される問題です。知識の必要性に関して、やや強く必要です。合同式を数列で運用する知識、7のn乗倍数の表し方など、難しめの知識が必要です。
問1に関して、数列{an}の初項~第600項のうち「7の倍数である項の数」を答えます。
ポイントは「anが7の倍数となる条件を書き出す」ことです。
それは「an≡0(mod7)」です。
- 条件より
an=4n-3 - anが7の倍数の時
an≡0(mod7)
∴ 4n≡3≡24(mod7)
4と7は互いに素なので
n≡6(mod7) - 今、自然数kを用いて
n=7k-1
と表すと
1≦n≦600
より
1≦7k-1≦600
∴ 2/7≦k≦601/7 - kは自然数なので
1≦k≦85
より、7の倍数となる項は
85個
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2に関して、数列{an}において「7²の倍数である項の数」を答えます。
ポイントは「anを7でくくること」です。
問1で「7の倍数項」を求めたので、これを応用します。7で括ったカッコ内が更に7の倍数になる、という条件で立式すると「7²の倍数」となります。
- 問1より
anが7の倍数になる時
an=4(7k-1)-3
=7(4k-1)(k=1,2,…,85)
と書くことができる - この条件の下に
(4k-1)が7の倍数となれば
anは7²の倍数となる - この時
4k-1≡0(mod7)
∴ 4k≡1≡8(mod7)
4と7は互いに素なので
k≡2(mod7) - 今、自然数lを用いて
k=7l-5
と表すと
1≦k≦85
より
1≦7l-5≦85
∴ 6/7≦l≦90/7 - lは自然数なので
1≦l≦12
より、7²の倍数となる項は
12個
(これが正解です)
合格者さんでも一定数の不正解者が出るレベルです。
よって、正解できれば他者に差をつける1問です。
問3に関して、数列の積(a₁a₂…an)が「7⁴⁵の倍数となる最小の自然数n」を答えます。
- 問2より
anが7²の倍数になる時
an=7{4(7l-5)-1}
=7²(4l-3)(l=1,2,…,12)
と書くことができる - この条件の下に
(4l-3)が7の倍数となれば
anは7³の倍数となる - これを満たすlは
l=6
のみである
| l | 6 |
| k | k=7l-5より k=7×6-5=37 |
| n | n=7k-1より n=7×37-1=258 |
上表より、anが7³の倍数になるのは「n=258」の時です。
| an | kの値 | nの値 |
|---|---|---|
| 7²の倍数 | 2,9,16,23,30,37,44,51,58,65,72 | 13,62,…,258,…,503 |
| 7¹の倍数 | 1,2,3,…,37,…,85 | 6,13,20,…,258,…,594 |
7²の倍数・7¹の倍数が上表の通りなので、これらをヒントに7⁴⁵まで数えれば正解です。
- 以上より、n=258の時
積a₁a₂…a₂₅₈が持つ因数は
7³が1つ
7²が6つ
7¹が37つ
なので、因数7の個数は
37+6+1=44
となる - よって、7⁴⁵になるのは
n=258の次の7の倍数
すなわちn=265である
(これが正解です)
医学科の合否を分ける1問です。
医学科・臨床科以外の受験生さんは、解かなくてよいです。
受験生としての解説
2017年の九大数学5問で、1番難しい問題です。
小問1に関して、一般項「an=4n-3」を求め、7を法とする合同式を書き、合同式を満たすnの条件から正解を導く、というのは不合格者さんには厳しく、合格者さんはやり遂げてくるレベルです。よって、小問1は合否を分ける1問となります。
小問2に関して、小問1で求めた「anが7の倍数になるnの条件」を「数列anの式」に戻して7でくくり、くくったカッコの中身が「更に7の倍数」になる条件を求めるというのは、非医歯薬系の合格者さんでも難しい事です。よって、小問2は正解できれば他者に差をつけられる1問となります。
小問3に関して、小問2の条件を更に発展させ、7でくくったカッコの中身を更に7でくくり、そのカッコ内が7の倍数になる条件を求める事は大変です。その上で「因数7」の数が45個になるまで数えていく事は大変なので、これは「医学科の合否を分ける1問」とみなしてよいでしょう。
2017年の九大数学は
- 大問1「積分」がやや簡単
- 大問2「空間ベクトル」が簡単
- 大問3「数列」が難しい
と、難易度に差があります。配点は全て50点ずつなので、いかに大問1・大問2を確実に正解する事が大切か解ります。九大数学は大問5つから「2完答+3部分点」で合格できます。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや強めに必要)
- 知識:★★★★(やや難しい)
- 総合:★★★★(やや難しい)
- 短評:問1を確保したい
大問4

講師としての解説
「数列」と「場合の数・確率」からの出題です。
計算量・難易度に関して、やや簡単です。確率と数列を組み合わせたシンプルな計算が続きます。閃きの必要性に関して、やや簡単です。問2で与式を見て「n-1回目までゲームが終わらない確率」と発想を転換する部分や、問3の式変形などで少し工夫があります。知識の必要性に関して、やや簡単です。場合の数で「C」の計算ができること、数列で漸化式を立てられること等が必要です。
問1に関して、確率計算です。Aが「4回目に勝つ確率」と「7回目に勝つ確率」を答えます。Aが4回目に勝つためには、少なくともAが4回目に球を引く必要があります。それが起きるのは
- 球を引く権利が3回連続で移動しないパターン
- 球を引く権利が3回連続で移動するパターン
の2つです。よって、各々について確率計算すれば正解できます。
問2に関して、確率計算です。求める「dn」は「n回目の勝負が始まる確率」を表しています。逆に言えば「n-1回目までに勝負が終わらない確率」なので「1/2^n-1」となります。
問3に関して、漸化式を立てる問題です。Aの「n-2回目」と「n+1回目」の間にある関係を漸化式で表します。「n+1回目にAが球を引く確率」について「n-2回目」の状態からパターンを探りましょう。
| n-2回目に 球を引く人 | 必要な玉の出方 | 確率 |
|---|---|---|
| A | 3連続白 3連続青 | 1/4^3 + 1/4^3 |
| B | 青が1個 白が2個 | 3C1・1/4・1/4^2 |
| C | 青が2個 白が1個 | 3C2・1/4^2・1/4 |
「n-2回目」に球を引くのはA・B・Cの3パターンなので、この3パターンについて確率計算し、小問2の「dn」を応用して式変形すれば正解です。
受験生としての解説
2017年の九大数学5問で、3番目の難易度です。
小問1に関して、シンプルな確率計算なので不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問2に関して、「dn → n-1回目までにゲームが終わらない確率」という発想の転換は、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問3に関して、確率に関する漸化式を立てる事は簡単ではありませんが、その中でも本問は簡単な部類です。合格者さんは確実に正解してくるレベル、不合格者さんには一定数の不正解者が出るレベルなので、合否を分ける1問です。
九大受験における「場合の数・確率」は、時間をかけて手探りするほど正解に近づけます。よって
- 簡単な大問1・大問2を完答
- 大問4に時間を多めに使って厚く部分点
- 難しい大問3・大問5から薄く部分点
という流れで簡単な順に得点していけば、戸畑高校で落ちこぼれて退学になるような学生さんでも九大合格できます。
- 計算:★★(やや簡単)
- 閃き:★★(やや簡単)
- 知識:★★(やや簡単)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問5
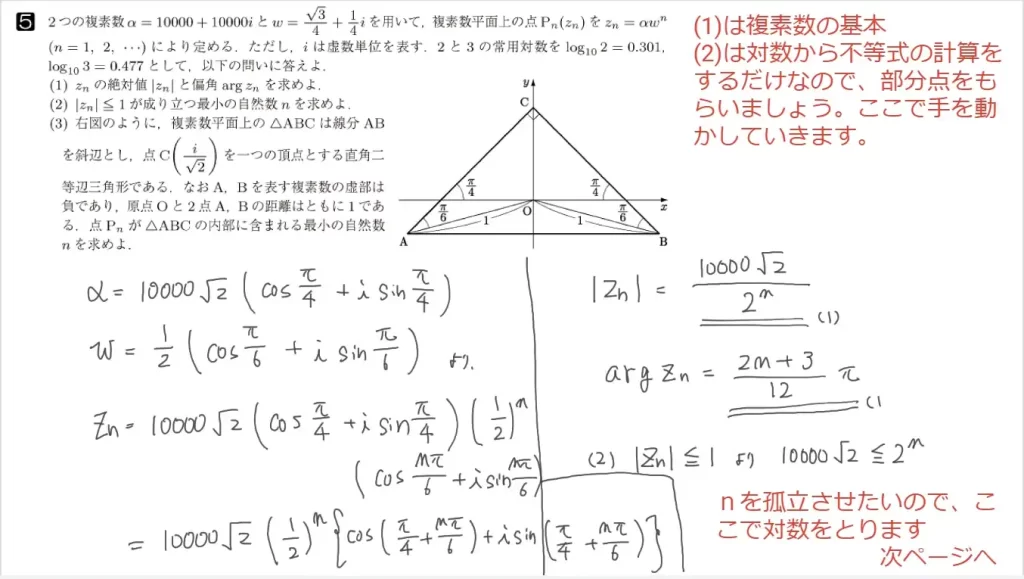
講師としての解説
「複素数平面」からの出題です。
計算量・難易度に関して、やや難しいです。ド・モアブルの定理、対数計算、不等式による評価などがあります。閃きの必要性に関して、やや多めに必要です。小問3のシチュエーションは問題集であまり見かけないため思考を要します。知識の必要性に関して、普通程度です。複素数平面の基礎知識、対数計算、不等式による評価を使います。
問1に関して、複素数znの絶対値・偏角を答えます。複素数「zn=αw^n」を構成する「α」と「w」は問題文で与えられています。両方とも「絶対値×偏角」の形へ式変形し「α×w^n」でかけ算すれば、znが求まって正解となります。
問2に関して、|zn|≦1が成り立つ最小の自然数nを求める問題です。|zn|は既に問1で求めています。よって代入し、分母を右辺へ送ると「10000√2≦2^n」となります。「最小のnを求めよ」という指示なのでnを孤立させたい・・・そこで両辺に「log」を使います、底は10です。後は式変形をして左辺をnだけ(n≧・・・の形)にすれば「n≧13.7」となり「自然数nの最小は14」で正解となります。
問3に関して、点Pnが三角形ABCの内部に含まれる時の、nが取りうる最小値を求めます。問2の結論より「nは14以上」と判っているので、n=14、15、16・・・と小さい順に代入して正解を探します。nの値によって「zの絶対値・偏角」が確定するので、三角形ABCと比較していくとn=15が正解と解ります。
受験生としての解説
2017年の九大数学で、2番めに難しい大問です。
小問1に関して、複素数を「絶対値×偏角」に式変形するだけなので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問2に関して、急に対数を使う事は少し難しいですが、問1の直後に問2の問題文で「|zn|≦1」と指定するのは、かなり解りやすい誘導です。よって、不合格者さんでも正解してくるので、全ての受験生さんが正解したい問題です。
小問3に関して、問題集で練習する事が難しい、本問独特のシチュエーションです。よって、合格者さんでもやや厳しいレベルなので、正解できれば他者に差をつける1問となります。その場の応用力(=頭の良さ、才能)もしくは、本問を「普通」と感じられるほどのハイレベルな訓練(医学科対策)が必要なので、非医歯薬系の受験生酸は不正解で構いません。
2017年は
- 大問1・大問2・大問4が簡単
- 大問3は計算が複雑
という事で、おそらく時間に追われいるでしょう。簡単な順に得点してください。難しい問題を捨てても、非医歯薬系の合格得点率56%に届きます。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:小問2まで正解したい
九州大学の数学2016年・平成28年度
大問1

講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、普通程度です。難しい計算はありませんが、小問3で極限を求めるために一工夫あります。閃きの必要性に関して、ほぼ必要ありません。問題集のコピーの様な問題です。知識の必要性に関して、やや簡単です。「1/6公式」と「logの極限」が必要ですが、いずれも基本的なものです。
問1に関して、証明問題です。aをnの式で表し、a>1を示します。曲線C1・C2の式からyを消去し、x=n+1を代入すれば、「a=」の形を作れて正解となります。続いて、aの式の右辺をf(x)と置き、f(x)が単調増加する事を微分で調べ、端点x=1においてa>1となる事を示せば証明完了です。
問2に関して、面積計算です。領域SnとTnの面積を答えます。まずSnに関して、y=logxを積分した面積から「下側の三角形」を引くと正解できます。続いてTnに関して、「1/6公式」を使って積分すれば正解できます。
問3に関して、極限値の計算問題です。与式で提示された極限値を答えます。与式がやや複雑ですが、怖がる必要はありません。
- 与式を組む
- 約分する
- 何が極限値の計算を邪魔しているか見つける
- 邪魔しているものに焦点を当てて処理する
この手順で正解できます。
受験生としての解説
2016年の九大数学5問で、1番簡単な問題です。
小問1に関して、交点の座標からaの値を求める事、「a=f(x)」の形をとり「f(1)>1」と単調像から「a>1」を証明する事、いずれも不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問2に関して、「logの積分」をして三角形を引くだけのSn、「1/6公式」を使うだけのTn、いずれも不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問3に関して、式変形が難しく、不合格者さんの中には解けない人もいるが合格者さんは正解してくるレベルです。よって、合否を分ける1問となります。式全体を見ると難しいですが、「極限値をジャマしているものを消す」という意識を持っておくと、自然と正解にたどり着けるようになります。
九大数学は5つの大問から「2完答+3部分点」で非医歯薬系の合格得点率56%を作れます。本問を完答しておけば、残り4問から「1完答+3部分点」で済みます。そうなれば、熊本大学の合格者がほとんど出ない「2番手高校」の学生さんでも九大合格できます。難しい問題を避け、簡単な問題を確実に拾いましょう。才能の無い学生さんでも、才能の差を補って九大合格できます。
- 計算:★★★(普通)
- 閃き:★(ほぼ不要)
- 知識:★★(やや簡単、1/6公式)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問2

講師としての解説
「平面図形」からの出題です。
計算量・難易度に関して、簡単です。メネラウスの定理による分数計算がある程度です。閃きの必要性に関して、普通程度に必要です。小問4で三角形PQRを抜き出す際に一工夫あります。知識の必要性に関して、やや簡単です。しかし、九大受験生が手薄にしがちな「メネラウスの定理・チェバの定理」なので油断できません。
問1に関して、計算問題です。三角形の各頂点から伸ばした線分が1点で交わるシチュエーションです。よって、チェバの定理そのままで正解となります。
問2に関して、線分の長さの割合を求める問題です。メネラウスの定理そのままで正解となります。⊿ACEと直線BFにメネラウスの定理を用いると「AP:PE=3:t」と判り、kが求まります。同様に⊿BCD直線AEにメネラウスの定理を用いると「CR:RD=(3-3t):2t」と判り、lが求まります。
問3に関して、面積計算です。⊿BCQと⊿BCFは各々の底辺BQ・BFとみなすと高さが等しいため、BQ:BFがそのまま面積比を表します。よって⊿ABFと直線CDにメネラウスの定理を用いて「BF:BQ=3:2」と判り「⊿BCQ=⊿ABC×1/4×2/3=1/6」で正解となります。
問4に関して、面積計算です。ポイントは「⊿PQRを抜き出すこと」です。⊿PQRを直に計算しようとせず、問3の要領で⊿BCQ・⊿ACR・⊿ABPの面積を求めてください。後は「⊿PQR=⊿ABC-(⊿BCQ+⊿ACR+⊿ABP)」で正解となります。
受験生としての解説
2016年の九大数学5問で、3番目の難易度です。
小問1・小問2に関して、チェバの定理・メネラウスの定理そのままなので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問3に関して、⊿BCQが⊿BCFの一部である事は不合格者さんでも気づきます。そして、問2のおかげでメネラウスの定理を使う発想も持っています。よって、不合格者さんでも正解してくるので、全ての受験生さんが正解したい問題です。
小問4に関して、「⊿PQRを抜き出す」という発想は不合格者さんには難しく、合格者さんには丁度できるというレベルです。よって、合否を分ける1問となります。
九大受験生が手薄にしがちな「メネラウスの定理・チェバの定理」からの出題という事で、忘れていた場合は大問丸ごと0点になってしまいます。一方で、問題自体は簡単なので満点も取りやすいという、かなり怖い出題でした。
数学に限らず英語・物理・化学でも、九州大学で珍しい分野が出題された際は、難易度が大きく下がる傾向にあります。具体的には「基本事項の確認問題」だけで合格点を取れる場合が多いです。この様な分野を練習しておけば、才能の無い学生さんでも、才能の差を補って九大合格できます。
- 計算:★(簡単)
- 閃き:★★★(普通、小問4で一工夫)
- 知識:★★(やや簡単、メネラウスの定理)
- 総合:★★(やや簡単)
- 短評:満点にも0点にもなりやすい怖い1問
大問3

講師としての解説
「確率」と「数列」からの出題です。
計算量・難易度に関して、簡単です。計算らしい計算はありません。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。知識の必要性に関して、やや少ないです。確率に関する漸化式を立てられれば十分です。
問1に関して、確率計算です。サイコロを2回投げた後、コインがP0の位置に戻る確率を答えます。1回目にどの目が出ていようと、2投目でコインがP0へ行くサイコロの目は1つです。よって「1/6」が正解となります。
問2に関して、確率計算です。サイコロを3回投げた後、コインがP0の位置に戻る確率を答えます。問1と同様、2回目終了後にコインがどの位置にあろうと、3回目のサイコロでP0に戻る目は1つです。しかし、問1の様に「最後の1投の直前の状態」を書き出そうとすると、サイコロ2投で6×6=36パターンもあるため大変です。そこで、数学の技術を使います。サイコロを2回投げた後
- P0にある状態(問1の正解なので確率1/6)
- P0にない状態(確率1-1/6=5/6)
に分けて考えると、2パターンの計算で正解できます。いずれの場合も、サイコロ3投目でコインがP0に戻る目は1つなので「1/6×1/6+(1-5/6)×1/6」と立式でき、正解は「1/6」です。
問3に関して、確率計算です。サイコロをn回投げた後、コインがP0の位置に戻る確率を答えます。「n回目」なので全パターン書き出す作戦は使えません。よって問2を応用し、サイコロをn-1回投げた後
- P0にある状態(pn-1とおく)
- P0にない状態(すると1-pn-1となる)
に分けて考えます。いずれの場合も、サイコロn投目でP0に戻る目は1つなので「pn-1×1/6+(1-pn-1)×1/6」と立式でき、正解は「1/6」です。
受験生としての解説
2016年の九大数学5問で、2番めに簡単な問題です。
小問1・小問2に関して、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問3に関して、合格者さんは正解するが、不合格者さんの一定数が正解できないレベルです。よって、落とすと痛い1問となります。
よって、完答したい大問です。「場合の数・確率」が苦手で、小問3の漸化式を立てられない受験生さんでも、小問2までは部分点を拾っておきましょう。サイコロ3回の出目は全部で216パターンしかないので、全て書き出す事は可能です。
- 計算:★(簡単)
- 閃き:★(ほぼ不要)
- 知識:★★(やや簡単)
- 総合:★(簡単)
- 短評:完答したい1問
大問4

講師としての解説
「整数」からの出題です。
計算量・難易度に関して、普通程度です。合同式の計算が続きますが難しくはありません。閃きの必要性に関して、普通程度です。出題がやや独特なので合わせる必要があります。知識の必要性に関して、普通程度です。整数問題で定番の「桁ごとに分解する」解法を使います。
問1に関して、証明問題です。問題文の
- 「an+1は、10anを13で割った余りに等しい」とは
- 「10の(n+1)乗を13で割った余りは、10anを13で割った余りに等しい」という事なので
anに関する式「10^n ≡ an」の両辺を10倍すれば、どうにかなりそうな気がします。実際にやってみると「10^n+1 ≡ 10an」となり、立式した時点で証明終了となります。
問2に関して、計算問題です。問題文には「a1、a2、・・・a6、を求めよと書いてありますが、要するに10、100、1000、・・・1000000まで13で割った余りを求めればよいです。よって
- 10^1を13で割った余り・・・余り10=a1
- 10^2を13で割った余り・・・「100=13×7+9」より、余り9=a2
- 10^3を13で割った余り・・・「1000=13×76+12」より、余り12=a3
- 10^4を13で割った余り・・・「10000=13×769+3」より、余り3=a4
- 10^5を13で割った余り・・・「100000=13×7692+4」より、余り4=a5
- 10^6を13で割った余り・・・「1000000=13×76923+1」より、余り1=a6
と計算すれば、小学生でも正解できます。小問1の関係式を小問2に応用できない人でも点数を拾えます。
【模範解答(小問1を小問2で応用)】
- 10=13×0+10より、a1=10
- 10^2≡10a1なので、100=13×7+9より、a2=9
- 10^3≡10a2なので、90=13×6+12より、a3=12
- 10^4≡10a3なので、120=13×9+3より、a4=3
- 10^5≡10a4なので、30=13×2+4より、a5=4
- 10^6≡10a5なので、40=13×3+1より、a6=1
問3に関して、合同式の応用問題です。「◯2016▲」という6桁の整数の内、13で割り切れるものを答えます。
- 自然数N=b2016c(1≦b≦9、0≦c≦9)と置く
- N=b・10^5+2・10^4+1・10^2+6・10^1+cなので
- N≡b・a5+2・a4+1・a2+6・a1+c≡4b+c-3≡0(mod13)
- 4b+c≡3
- よってこれを満たす(b,c)=(2,8)(3,4)(4,0)(5,9)(6,5)(7,1)(9,6)が正解
上記が模範解答です。各桁をバラバラにして足し算で表しす定番です。これに問1・問2を応用して合同式を加えると、正解を示す合同式を得られます。
【小学生でも正解できる方法】
- 120160÷13=9243余り1
- 120161÷13=9243余り2
- ・・・
- 120169÷13=9243余り10
- よって、左端が1の時、13で割り切れる数は無い
- 220160÷13=16935余り5
- ・・・
- 220168÷13=16936余り0
- よって(2,8)が正解の1つ
- 320160÷13=24627余り9
- 以下ず~っと割算で、総合90回ぐらいですが「余りが1ずつ増える」ので、実際は10回ほどで済みます
- 920169÷13=70782余り3
- よって(2,8)(3,4)(4,0)(5,9)(6,5)(7,1)(9,6)が正解
受験生としての解説
2016年の九大数学5問で、1番難しい問題です。
小問1・小問2に関して、不合格者さんでも正解してくるレベルなので、全ての受験生さんが正解したい問題です。
小問3に関して、模範解答の「ケタ数ごとに分解して解く方法」は整数問題の定石ですが、不合格者さんには難しいです。合格者さんは正解してくるので、合否を分ける1問です。よって「小問3を小学生でも正解できる解き方」が重要です。
- サイコロの出目を全パターン書き出したり
- x=1から順に値を入れて「金庫破り」したり
- 本問の様に強引に計算で突破したり
九大数学の「場合の数・確率」は必ずしも「正規の解き方」を使わずとも正解を出せる場合があります。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:完答したい1問
大問5

講師としての解説
「複素数平面」からの出題です。
計算量・難易度に関して、普通程度です。ドモアブルの定理を使った複素数の計算、三角関数の計算があります。閃きの必要性に関して、やや少ないです。式変形を続けていく問題ですが、テクニカルな式変形はありません。知識の必要性に関して、やや少ないです。ドモアブルの定理、三角関数の公式を使えれば正解できます。
問1に関して、証明問題です。問題文で「zの式」が与えられており、問1の問題文で「zのn乗」「zの-n乗」を使う事もわかっています。よって、ド・モアブルの定理から
- z^n=cosnθ+isinθ
- z^-n=cos(-n)θ+isin(-n)θ
とします。式を整えて
- z^n=cosnθ+isinnθ・・・①
- 1/z^n=cosnθ-isinnθ・・・②
「①+②」と「①-②」で証明完了です。
問2に関して、2倍角・3倍角の公式より
- cos2x=2cos²x-1
- cos3x=4cos³x-3cosx
与式に代入、全ての項を「cosx」で統一すれば
- 2cos³x-cos²x-2cosx+1=0
- (cosx-1)(cosx+1)(2cosx-1)=0
0≦x≦2πより
- cosx=-1,1/2,1
- x=0,1/3π,π,5/3π(これが正解です)
問3に関して、まず半角公式でsinの「2乗」を消します。
- 与式=(1-cos40°)/2+(1-cos80°)/2+(1-cos120°)/2+(1-cos160°)/2
- =2-1/2(cos40°+cos80°+cos120°+cos160°)・・・③
「cos120°=-1/2」なので、残りを処理します。和積の公式より
- cos40°+cos160°
- =2cos(40°+160°)/2・cos(40°-160°)/2
- =cos100°
- =cos(180°-80°)
- =-cos80°・・・④
④を③に戻せば
- 与式=2-1/2(-cos80°+cos80°-1/2)
- =9/4(これが正解です)
受験生としての解説
2016年の九大数学5問で、2番めに難しい問題です。
問1に関して、ドモアブルの定理で「zのn乗・-n乗」を出し足し算・引き算するだけなので、不合格者さんでも正解してきます。よって全ての受験生さんが正解したい問題です。
問2に関して、2倍角・3倍角の公式を使うだけです。その後の因数分解も「cosx=1」が明らかなので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
問3に関して、不合格者さんにはやや難しいですが、合格者さんは正解してくるレベルなので、合否を分ける1問です。
- 計算:★★★(普通)
- 閃き:★★(少し必要)
- 知識:★★(やや簡単)
- 総合:★★(やや簡単)
- 短評:完答したい1問
九州大学の数学2015年・平成27年度
大問1

講師としての解説
「積分」からの出題です。
計算量・難易度に関して、普通程度です。問3はやや煩雑な計算となりますが、難しくはありません。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。知識の必要性に関して、普通程度です。問2は「1/6公式」を使えれば素早く解けます。
問1に関して、直線lと曲線C1が異なる2つの交点を持つための「aの範囲」を求めます。まず問題文の条件から解ることは
- 直線lの式より、直線lは(-4,0)を必ず通る
- 曲線C₁の作図より、曲線C₁は「y=-x²+2x」のグラフの第1象限である
という事です。よって、問1の正解である「直線lの傾きの範囲」は
- 0以上
- 曲線C₁と直線lの接点まで
となります。よって「曲線C₁と直線lが接する条件」を求めれば正解できるので、判別式D₁として
- D₁=(a-2)²-16a=0
- ∴ a=10±4√6
- 作図よりa=10-4√6の時が「第1象限の接点」と解るので
- 正解は「0≦a<10-4√6」です
問2に関して、面積計算です。曲線C₁と直線lで囲まれた面積S₁を求めます。まず、問題を見た感じ「おそらく1/6公式を使うだろう」と解るので、曲線と直線の2交点をα・β(α<β)と起きます。曲線C₁と直線lの式から「yを消去した方程式」の2解がα・βなので、この式に解の公式を使うと
- α=-(a-2)-√a²-20a+4
- β=-(a-2)+√a²-20a+4
となります。よって「1/6公式」を使うと
- S₁=∫{(-x²+2x)-a(x+4)}dx(積分範囲:α~β)
- =-∫(x-α)(x-β)dx
- =1/6(β-α)₃(←1/6公式)
- =1/6(√a²-20a+4)³(これが正解です)
問3に関して、証明問題です。「S₁=S₂なるaが存在する事」を証明するので、まずS₂を求めます。
- 問2のS₁と全く同じプロセス(交点をγ・δと置き、1/6公式に持ち込む)なので、計算を省略します
- S₂=4/3 – 1/6(√a²-12a+4)³
続いて、「S₁=S₂なるaが0<a<1/5の範囲に存在する」事を示します。
- S₁=S ₂の式を左辺に集めると「(√a²-20a+4)³+(√a²-12a+4)³-8=0」
- f(a)=左辺と置くと
- f(a)は0≦a≦1/5の範囲で連続であり
- f(0)=8>0
- f(1/5)=(-999+41√41)/125
- <(-999+41×7)/125
- =-712/125<0
- よって中間値の定理より、f(a)=0を満たすaが0<a<1/5の範囲に少なくとも1つ存在する事を示せた(証明終了)
受験生としての解説
2015年の九大数学で1番簡単な問題です。
小問1に関して、曲線と直線が共有点を持つ条件は作図から明らかなので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問2に関して、1/6公式に持ち込む事が解りやすいので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問3に関して、小問2と同様の方法でS₂を導き、「S₁=S₂」と立式する所までは不合格者さんでもやってきます。ここから中間値の定理に持ち込む部分が不合格者さんには厳しいです。合格者さんは正解してくるレベルなので、合否を分ける1問です。
九大数学は5つの大問から「2完答+3部分点」で非医歯薬系の合格得点率56%を作れます。合格点を取るだけなら大問1・大問2のレベルで可能なので、難しい事は避け、簡単な事を確実に正解してください。
- 計算:★★★(普通)
- 閃き:★★(やや簡単)
- 知識:★★(やや簡単)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問2

講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、普通程度です。問2までは簡単ですが、問3の不等式で一工夫あります。閃きの必要性に関して、少ないです。問題集のコピーの様な問題です。知識の必要性に関して、少ないです。問1・問2は基本レベル、問3は少し難しい計算ですが定番です。
問1に関して、証明問題です。与式が単調減少する事を示すので「微分<0」に持ち込みます。よって、まず与式を微分すると
- y’=-(logx+2)/x²(logx)³
- x>1においてlogx>0より
- y'<0(証明完了)
となります。
問2に関して、不定積分の計算問題です。与式の「1/x」に注目してください。「(logx)’=1/x」なので、この積分計算は「真っ直ぐ計算できる」と解ります。
- 与式=∫(logx)’/(logx)² dx
- =-1/logx +C(Cは積分定数)
となります。
問3に関して、証明問題です。
- 問2で行った積分が「滑らかな面積計算」
- 問3の左辺が「ブロックを組み合わせた面積」
という事で、積分による「滑り台の面積」とシグマ記号による「階段の面積」の比較問題です。問1で「y=1/x(logx)²が単調減少である」事を示しているため、以下の関係が成り立ちます。
- k-1≦x≦k(k=3,4,5…)の時
- 1/k≦1/x
- 1/k(logk)²≦1/x(logx)²
上式の両辺は、グラフにおいて、「x=kの時のy座標」と「x=xの時のy座標」を表しているため「x軸からの高さ」を比較していると言えます。つまり「針の長さ」を比較しているようなものです。
針の長さで「1/k(logk)²≦1/x(logx)²」が成り立つなら、針に「横幅1」を与えて「長方形の面積」にしても、同じ関係が成り立つのではないか?という事でインテグラル(∫)をつけます。
- ∫1/k(logk)²dx<∫1/x(logx)²dx(∫の積分区間は「k-1~k」で幅1です)
- 左辺は簡単に計算できる(xが無い)ので、左辺だけ計算すると
- 1/k(logk)²<∫1/x(logx)² dx
これで針に「幅1」を与えて長方形にしても、上の関係が維持されると解りました。
ならば今度は、「幅1」と言わず、一定区間を与えて「幅3~n」にしたらどうだろう?という事で、シグマ記号を使って「3~n」まで集めます。
- ∑1/k(logk)²<∑∫1/x(logx)² dx
- 上式∫の積分区間は「k-1~k」、シグマ記号の区間は「k=3~n」なので
- 右辺=∫1/x(logx)² dx(∫の区間は2~n)
- =[-1/logx](区間は2~n)
- =1/log2 - 1/logn
- < 1/log2(証明完了)
となります。
受験生としての解説
2015年の九大数学5問で、3番めの難易度です。
小問1に関して、微分して「y’<0」を示すだけなので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問2に関して、「(logx)’=1/x」だから「与式の積分計算は簡単に終わる」という事は、不合格者さんでも気づけます。よって、全ての受験生さんが正解したい問題です。
小問3に関して、「区分求積法」による面積比較は、合格者さんでも一定数が不正解になるレベルです。よって、正解できれば他者に差をつける1問となります。
小問1・小問2を落とさないでください。小問3は正解できなくても「非医歯薬系の下位~中位合格」ならできます。小問3は問題集「区分求積法」のやや簡単な応用なので身につけてほしいですが、英語・物理・化学の勉強を考えると簡単ではないでしょう。5科目トータルで九大合格を考えるなら、落とせるレベルです。
- 計算:★★★(普通)
- 閃き:★★(少し必要)
- 知識:★★(少し必要)
- 総合:★★★(普通)
- 短評:なるべく完答したい
大問3

講師としての解説
「積分」からの出題です。
計算量・難易度に関して、普通程度です。積分による体積計算では、計算過程が複雑になる事が普通ですが、その中ではシンプルな方です。閃きの必要性に関して、やや強く必要です。医学科の受験生さんにとっては「知識」の範囲ですが、非医歯薬系の受験生さんだと「閃き」に頼る部分は強いです。知識の必要性に関して、普通程度です。作図と積分計算ができれば十分です。
問1に関して、計算問題です。「y座標の範囲をkを用いて示せ」と難しく書いてありますが、要するに「影の両端の座標」を見つければ正解です。左右1つずつ、丁寧に出していけば簡単です。上画像の様に⊿ABCを設定して考えます。
【影の左端】ドームが地面と接する部分
- ドームの底円の方程式:x²+y²=1
- 今、x=kなる平面でドームを切った「切り口」を考えるので
k²+y²=1 - yでまとめて
y=±√1-k² - 上の画像より「y>0」なので
y=√1-k²=影の左端の座標
【影の右端】ドームをかすめた太陽光が地面に当たる部分
- ACsinπ/6=AB
- ∴ AC=2AB
- 上の画像より「AB=影の左端の座標」なので
AB=√1-k² - よって
影の右端の座標=AC=2AB=2√1-k²
正解は「影の左端<y<影の右端」なので、「√1-k²<y<2√1-k²」となります。
問2に関して、面積計算です。問1で求めた影を「-1<k<1」の範囲で積分するだけです。
- ∫(影の長さ)dk (-1<k<1)
- =∫(線分AC)dk-(ドーム底円の右半分)
- =\(\int _{-1}^{1}2 \sqrt{1-k^{2}}dk\)-π/2
- =2(半径1の円の上半分)-π/2
- =π/2(これが正解です)
問3に関して、体積計算です。問1で求めた「影の長さ」を「影の面積」にすれば正解できます。影の面積をx軸方向に積分すれば、体積が求まって正解となります。
受験生としての解説
2015年の九大数学5問で、2番めに難しい問題です。
問1に関して、ドームの底円「x²+y²=1」に「x=k」を代入して「y=√1-k²」とする部分が不合格者さんには難しく、合格者さんは突破してきます。よって、合否を分ける1問です。
問2に関して、問1さえ突破できれば不合格者さんでも正解できる問題です。よって、問1とセットで、合否を分ける1問です。
問3に関して、問1・問2が正解できた人にとっては「問3も本質的に同じ」と解るので、不合格者さんでも正解できるレベルです。よって、問1とセットで、合否を分ける1問です。
積分による「空間図形の体積」を求める問題は、九州大学の定番です。ここを得意にしておけば
- 簡単な大問2つ+体積計算=3完答
- 簡単な大問1つ+体積計算=2完答
という事で「簡単な大問」が1つの年でも、2つの年でも、「2完答+3部分点=得点率56%」の安定感が増します。
頭の良い学生さんに有利な「整数・数列・複素数」などと異なり、微分積分は才能が無くても練習すれば解けるようになります。才能が無い学生さんほど大事にしたい1問です。
- 計算:★★★(普通)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:九大の定番
大問4

講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、簡単です。基本的に分数のかけ算です。閃きの必要性に関して、普通程度です。問題のシチュエーションに合わせて解答方法を考えます。知識の必要性に関して、ほぼ不要です。優秀な中学生なら正解できます。
問1に関して、確率計算です。2回の操作後に硬貨をもらう条件は
- 1回目に赤球を引く・・・確率2/3
- 2回目も赤球を引く・・・確率1/3
なので、正解は「2/3 × 1/3 =2/9」となります。
問2に関して、証明問題です。自然数nに対し「2n-1回目の操作で硬貨をもらうことはない」・・・①ことを示します。
(ⅰ)n=1の時、袋の中の玉は(赤,青)=(2,1)なので
- 赤玉を引く:(2,1)→(1,2)
- 青球を引く:(2,1)→(3,0)
より、硬貨もらうことはありません。
(ⅱ)n=kの時、①が成り立つと仮定すると、2k-1回目の終了時点の袋の中身は(3,0)または(1,2)となるため、袋の玉の存在パターンは以下の様になります。
| 2k-1回目 | 2k回目 | 2k+1回目 |
| (3,0) | (2,1) | (3,0) |
| (1,2) | (0,3) 硬貨獲得 | (1,2) |
ゆえに、n=k+1の時も①は成り立ちます。
(ⅰ)(ⅱ)より、奇数回目の操作で硬貨をもらうことはありません(証明完了)
問3に関して、確率計算です。8回目の操作で初めて硬貨をもらう確率を答えます。7回目まで1度も「青玉が3個」の状態になってはいけないので
| 1回目 | 2回目 | 3回目 |
| (2,1) | (3,0) | (2,1) |
| (1,2) |
という具合に、奇数回目に袋の中身が(2,1)になる事を繰り返して、8回目に届かせる必要があります。上の流れを(ア)と名付けると、(ア)が起こる確率は「1/3×1/1+2/3×2/3=7/9」となります。
そして、7回目・8回目で「連続で赤玉を引き、硬貨をもらう確率」を(イ)とすると、(イ)が起こる確率は問1より「2/9」です。
よって、求める確率は(ア)が3回(イ)が1回なので「(7/9)³×2/9=686/6561」が正解です。
問4に関して、確率計算です。「8回の操作で硬貨を1回だけもらう確率」を答えます。問3との違いは、2回目・4回目・6回目に硬貨をもらってもよい点です。よって、その場合は
| 偶数回目 | 奇数回目 | 偶数回目 |
| (0,3) 硬貨獲得 | (1,2) | (2,1) |
というプロセスを経て(2,1)の状態に復帰する必要があります。この流れを(ウ)と名付けると、(ウ)が起こる確率は「1/1×2/3=2/3」となります。よって
- 2回目に硬貨をもらう確率(イウアア)=2/9 × 2/3 × 7/9 × 7/9=588/6561
- 4回目に〃(アイウア)=588/6561
- 6回目に〃(アアイウ)=588/6561
- よって、求める値=686/6561 + 588/6561 ×3=2450/6561(これが正解です)
受験生としての解説
2015年の九大数学5問で、2番めに簡単な問題です。
問1に関して、不合格者さんでも正解してくるので、全ての受験生さんが正解したい問題です。
問2に関して、証明問題なので不合格者さんには難しい出題です。合格者さんは正解してくるので、合否を分ける1問です。
問3に関して、硬貨をもらうタイミングが「8回目」と確定しているので1回目・2回目・・・8回目と、計算でゴリ押しできます。よって、不合格者さんでも正解してくるので、全ての受験生さんが正解したい問題です。
問4に関して、硬貨をもらうタイミングが複雑になったため、不合格者さんには厳しい出題です。合格者さんは正解してくるレベルなので、合否を分ける1問です。
九大数学は全5問から「2完答+3部分点」で非医歯薬系の合格得点率56%を作れます。よって、2番めに簡単な本問は完答したい1問です。しかし「場合の数・確率」は個性の強い分野で、苦手とする受験生さんも多いです。本問を難しいと感じた場合は、ひとまず小問1だけは解き、大問2(3番めに簡単な大問)に移ってください。大問2も九大としては「普通~やや簡単」なので、完答を狙える1問です。
そして、概ね5つの大問を解き終わり、試験終了を待つだけの状態になったら大問4に戻り
- 小問2「証明問題」をあきらめ
- 小問3・小問4「8回の操作」を解いてください
小問3・小問4は「8回の操作」なので、玉の出入りは「2の8乗=256パターン」です。全パターン書き出せば小学生でも正解できます。
- 計算:★(簡単)
- 閃き:★★★(普通)
- 知識:★(ほぼ不要)
- 総合:★★(やや簡単)
- 短評:問2以外は正解したい
大問5

講師としての解説
「整数」からの出題です。
計算量・難易度に関して、やや難しいです。小問2までは簡単ですが、小問3で整数のやや難しい計算があります。閃きの必要性に関して、強く必要です。小問3を解く際に、小問1・小問2を応用する必要があります。それができた上で更に整数の計算を進め、何個あるかさえ解らない正解の組み合わせを全て答えます。知識の必要性に関して、普通程度です。整数問題の知識があれば十分です。
問1に関して、証明問題です。「2^n-1が3の倍数」である事を示すので、最終形は3(・・・)となるのでしょう。「nは正の偶数」と書いてあるので「n=2m、mは自然数」とおいてスタートです。
- 2^n -1
- =2-2m -1
- 4m -1
- (3+1)m -1
- =mC₀・3^n・1⁰+mC₁・3^m-1・1¹+・・・mCm・3⁰・1^m-1
- =3^m+mC₂・3^m-1+mC₂・3^m-2+・・・+mCm-1・3+1-1
- =3(3^m-1+mC₁・3^m-2+・・・+mCm-1)
となり、上式の括弧内は整数なので、与式はnが正の偶数の時3の倍数となります(証明終了)他には「数学的帰納法」を使っても証明できます。
問2に関して、証明問題です。「互いに素である事を示せ」なので「互いに素ではない」と仮定し、背理法に持ち込むのが良いです。
- 2^n+1と2^n-1が互いに素でないと仮定する
- 両者の最大公約数をdとおくと、dは2以上の自然数となり
- 2^n+1=da・・・①
- 2^n-1=db・・・②
- と書ける(a、bは互いに素な自然数でa>b)
- ①-②より、d(a-b)=2
- ∴ d=2、a-b=1となる
- ①にd=2を代入すると「2^n +1=2a」より「2^n=2a-1」
- 上式は左辺が偶数で右辺が奇数となり矛盾する
- よって、2^n+1と2^n-1は互いに素である(証明終了)
問3に関して、計算問題です。与式を満たす素数p・qの組み合わせを全て答える問題です(正解は1組です)
- 2^p-1 -1=pq^2・・・③
- (ⅰ)p=2の時
- 与式:2²⁻¹-1=2q²
- ∴ q²=1/2
- これを満たす素数qは存在しません
- (ⅱ)p≧3の時
- pが3以上の素数の時、p-1は正の偶数となります
- p-1が正の偶数という事は、問1の結果より「③の左辺=3の倍数」となります
- よって、③の右辺=pq^2=3k(kは自然数)と書けます
- 今、問題文より「pとqは異なる素数」なので
- p=3 または q=3です
- p=3を③に代入すると
- 2³⁻¹-1=3q²
- ∴ q²=1
- ですが、qは素数なので不適です。
- よって、pは「5以上の素数」と確定し、よって「q=3」と確定します
- これらを③に戻すと
- 2^p-1 -1=9p
- p-1は正の偶数なので、p≧5を考慮すると
- p-1=2r(rは2以上の自然数)とおけて
- 2^2r-1=9p
- ∴ (2^r)^2-1²=9p
- ∴ (2^r+1)(2^r-1)=9p
- 問2の結果より、2^r+1と2^r-1(≧3)は互いに素なので
- 2^r+1=9
2^r-1=p・・・④ - または2^r+1=p
2^r-1=9・・・⑤ - よって、④を満たす(r,p)=(3,7)
- ⑤を満たすrとpは存在しないため
- 正解は(p,q)=(7,3)となります
受験生としての解説
2015年の九大数学5問で、1番難しい問題です。
問1に関して、「n=2m」と置いて計算を進める事、「最終形は3(・・・)の形になること」が問題文から見えるので、不合格者さんでも一定数は正解してきます。よって、全ての受験生さんが正解したい問題です。
問2に関して、背理法に持ち込むことはすぐ思いつきたいところです。「互いに素である」と仮定した時に「最大公約数d」を置いて2つの数をつなぐ事も定番。置いた後 ~ 証明終了までの式変形もシンプルという事で、一見難しそうな問題ですが、正解したいレベルです。合否を分ける1問です。
問3に関して、問1・問2に比べ急激に難度が上がっています。「医学科の合否を分ける問題」なので、非医歯薬系の志望者さんは解けなくて大丈夫です。小問3を正解するより、英語・物理・化学の簡単な問題から点数を拾ってください。
- 計算:★★★★(やや難しい)
- 閃き:★★★★★(強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:小問3は医学科の合否を分ける問題
九州大学の数学2014年・平成26年度
大問1

講師としての解説
「積分」からの出題です。
計算量・難易度に関して、やや簡単です。部分積分と半角公式を使います。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。知識の必要性に関して、少ないです。接線の方程式、回転体の体積、いずれも基本です。
問1に関して、計算問題です。接線の方程式と接点の座標(a,b)を答えます。ポイントは「先に方程式を立ててしまうこと」です。x=aにおける接線の方程式を立て、それが(a,b)を通ると考えれば正解できます。
- f'(x)=1-cosxより
- 直線lの方程式は
- y-b=(1-cosa)(x-a) となります
- ∴ y=(1-cosa)x+acosa-a+b・・・①
- 題意より①の傾きが1/2なので
- 1-cosa=1/2
- ∴ cosa=1/2
- 今、0≦a≦π/2より
- a=π/3
- ∴ b=a-sina=π/3-√3/2
- よって(a,b)=(π/3,π/3-√3/2)(これが正解です)
- また①にa,bを代入して
- 直線l:y=1/2x+π/6-√3/2(これが正解です)
問2に関して、回転体の体積を求める問題です。
- V=∫πy²dx(積分区間は0→π/3)
- =π∫(x-sinx)²dx
- =π∫(x²-2xsinx+sin²x)dx
- =π(∫x²dx-2∫xsinxdx+∫sin²xdx)
ポイントは上記3つの積分計算を同時に行わず、1つ1つ丁寧に行う事です。
- ∫x²dx(積分区間は0→π/3)
- =[1/3x³]
- =π³/81・・・(A)
- ∫xsinxdx(積分区間は0→π/3)
- =[x(-cosx)]-∫(-cosx)dx(←部分積分です)
- =-π/3cosπ/3+[sinx]
- =-π/6+√3/2・・・(B)
- ∫sin²xdx(積分区間は0→π/3)
- =∫(1-cos2x)/2dx
- =1/2[x-1/2sin2x]
- =1/2(π/3-√3/4)・・・(C)
よって、上記(A)(B)(C)をVの式に戻して
- V=(π³/81+π/2-9√3/8)π(これが正解です)
受験生としての解説
2014年の九大数学5問で、1番簡単な問題です。
問1に関して、接線の方程式を立てて接点を求めるだけなので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
問2に関して、回転体の体積ですが、最も難しいのは「sin²xの積分」と「部分積分」です。この2つは不合格者さんでも正解してくるので、全ての受験生さんが正解したい問題です。
九大数学は出題5問から「2完答+3部分点」で非医歯薬系の合格得点率56%を作れます。本問は2014年の残り4問より簡単なので、完答を目指したいところです。本問を完答して残り「1完答+3部分点」の状態を作れば、才能の無い学生さんでも九大合格できます。
- 計算:★★(やや簡単)
- 閃き:★(ほぼ不要)
- 知識:★(少ない)
- 総合:★(簡単)
- 短評:完答したい1問
大問2

講師としての解説
「整数」からの出題です。
計算量・難易度に関して、やや簡単です。扱う数が3の倍数なので計算過程はややシンプルです。閃きの必要性に関して、やや強く必要です。整数問題なので、試験中に気づかねばならない要素は多めです。特に小問3は珍しい終わり方です(赤本・模範解答)知識の必要性に関して、やや少ないです。3の倍数に関する整数問題の経験があればよいです。
問1に関して、証明問題です。任意の自然数aの2乗を3で割った余りが0か1になる事を示します。ポイントは「3で割った」という部分です。自然数kを使い、aを「3k、3k-1、3k-2」の3パターンに場合分けして検証すれば正解できます。
- (ⅰ)a=3kの時
- a²=3・3k²より、3で割った余りは0となる
- (ⅱ)a=3k-1の時
- a²=(3k-1)²
- =3(3k²-2k)+1より、余りは1
- (ⅲ)a=3k-2の時
- a²=(3k-2)²
- =3(3k²-4k+1)+1より、余りは1
- (ⅰ)~(ⅲ)より題意を示せた(証明終了)
問2に関して、証明問題です。与式「a²+b²=3c²」を満たす自然数a・b・cが全て3の倍数である事を示します。ポイントは、唯一の具体的な数値である「3」です。
- 右辺「3c²」は3の倍数
- ∴ 左辺「a²+b²」も3の倍数
- ∴ 「a²」と「b²」は共に3の倍数(ここがポイント)
- 「a=3α、b=3β」とおくと
- 左辺=a²+b²=3²(α²+β²)=右辺=3c²
- ∴ c²=3(α²+β²)
- 上式よりc²は3の倍数であり、それはcが3の倍数である事を意味する
- よって、a・b・cは全て3で割り切れる(証明終了)
問3に関して、証明問題です。「実は、問2を満たすa・b・cは存在しない」ことを証明します。ポイントは、与式を満たすa・b・cが「1例たりとも存在しない」という強烈な条件です。「存在する」と仮定して計算を進めれば、強烈な矛盾が生じるはずです。その時点で正解となります。
- 問2より、自然数α・β・γを使って「a=3α、b=3β、c=3γ」と表すことができる
- 与式より、(3α)²+(3β)²=3(3γ)²
- ∴ α²+β²=3γ²
- 上式は、与式を「a→α、b→β、c→γ」と置き換えたものに等しい
- ゆえに、上式の関係を永久に続けられることになるが、自然数a・b・cは有限の値であるため矛盾する
- よって、与式を満たす自然数a・b・cは存在しない(証明終了)
受験生としての解説
2014年の九大数学5問で、3番めの難易度です。
問1に関して、任意の自然数aを「3k、3k-1、3k-2」の3パターンで表すことは、不合格者さんの一定数で不正解者が出るレベルです。よって、合否を分ける1問より、少し簡単な問題です。
問2に関して、「a²+b²が3の倍数」なら「a²」と「b²」も3の倍数、と気付く部分が不合格者さんには厳しいです。合格者さんは乗り越えてくるので、合否を分ける1問です。
問3に関して、「有限の値a・b・cを3で永久に割り続けられるから矛盾する」と導く部分は、合格者さんでもやや難しいです。よって、正解できれば他者に差をつける1問です。
2014年は、大問1・大問4が簡単です。よって、本問から高得点を取れば、大問1・大問2・大問4の3つだけで「非医歯薬系の合格得点率56%」に肉薄できます。
証明問題3連発という事で、苦手とする学生さんは多いですが、小問2までは頑張って正解したいところです。小問3に関して、九大合格レベルの学生さんなら「正解の直前」まではたどり着けます。しかし、正解への着地方法が独特なので、その点で苦労する人は多いでしょう。
逆に言えば、小問2まで解ければ九大合格できるので、才能の無い学生さんほど「小問2が解ける学力」を大事にしてください。
- 計算:★★(やや簡単)
- 閃き:★★★★(やや強く必要)
- 知識:★★(やや少ない)
- 総合:★★★(普通)
- 短評:小問2が合否の分かれ目
大問3

講師としての解説
計算量・難易度に関して、普通程度です。楕円と絶対値のついた図形の交点、最大値・最小値問題などやや煩雑な計算があります。閃きの必要性に関して、やや強めに必要です。最大値・最小値問題を解く際に図形的な考え方が必要となります。知識の必要性に関して、普通程度です。楕円、絶対値付きの図形、最大値・最小値問題の解き方などです。
問1に関して、値の範囲を求める問題です。直線と楕円が交点を持つためのaの条件を答えます。図形的な制約が無いので「判別式≧0」に持ち込んで大丈夫です。判別式≧0を解けば正解となります。
「接点は交点と言えるのか?」について。
問題文で指定が無いので、細かい部分は気にしなくて大丈夫です。「>」でも「≧」でもOKです。
問2に関して、作図問題です。|x|+|y|=1が表す図形を描きます。グラフにおける第1~4象限で絶対値の符号が変わります。正方形を45°傾けた図形が正解です。問3に関して、最大値・最小値問題です。問1で使った楕円に対し、問2で使った正方形を拡大・縮小し、交点を持つ範囲の最大値・最小値を求めます。拡大縮小に際して「=k」と置いて「kの最大値・最小値」で考える事は定石です。
- 最大値:正方形が楕円を飲み込む配置
- 最小値:楕円が正方形を飲み込む配置
で求まります。
受験生としての解説
2014年の九大数学5問で、2番めに難しい問題です。
小問1は「判別式≧0」で正解できるいつものパターンなので正解したいところです。小問2の作図も九大受験生なら問題ないでしょう。小問3に関して、問題集で類題の経験がある学生さんは、比較的楽に解けます。完全に初見の学生さんは、強く閃きが必要になるでしょう。
2014年は大問1・大問4が簡単なので、この2つを完答できている場合は、小問3にこだわり過ぎなくて大丈夫です。「2完答+3部分点」で非医歯薬系の合格ライン56%に届きます。
- 計算:★★★(普通)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:小問2までは正解したい
大問4
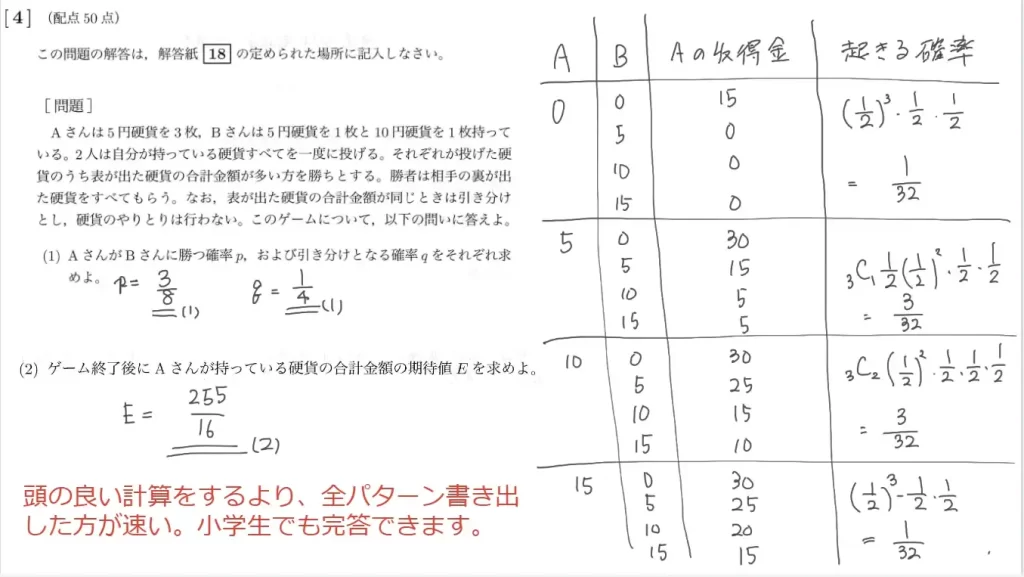
講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、簡単です。分数のかけ算があります。閃きの必要性に関して、やや弱いです。問題のシチュエーションを理解する必要はありますが、シンプルです。知識の必要性に関して、ほぼ不要です。優秀な中学生なら正解できます。
問1に関して、確率計算です。コイン投げゲームでAさんがBさんに勝つ確率・引き分ける確率を答えます。「場合の数・確率」は場合の数や確率に関する式を立て計算していく分野ですが、九大入試では頭を使わず、肉体労働で全パターン書き出せる場合がよくあります。計算で解けば才能のある頭の良い学生さんほど有利になりますし、一部でも計算が間違っていれば一気に0点になる危険も付きまといます。ならば、全て書き出してしまえば良いです。問2に関して、計算問題です。Aさんが獲得する金額の期待値を答えます。表に沿って期待値を足し算すれば正解できます。
受験生としての解説
2014年の九大数学5問で、2番めに簡単な問題です。
手探りしている内に「全パターン書き出した方が良い」と解れば、1番簡単な問題になります。本問を完答しておけば、残り大問4つから「1完答+3部分点」で非医歯薬系の合格得点率56%を作れます。
- 計算:★(簡単)
- 閃き:★★(少し必要)
- 知識:★(簡単)
- 総合:★(簡単)
- 短評:全パターン書き出すと速い
大問5

講師としての解説
「微分」からの出題です。
計算量・難易度に関して、普通程度です。論理展開の問題なので計算は難しくありません。閃きの必要性に関して、強く必要です。超難関や医学科用の特別な訓練を受けてない学生さんには、かなり閃きを要する問題です。知識の必要性に関して、やや強く必要です。平均値の定理、極値の条件、不等式の運用など、医学科用の問題集で見かけるタイプです。
誘導となる小問はありません。「極値を1つだけ持つ事の証明」なので
- f'(α)=0となるx=αが1つだけ存在する
- x=αの前後でf'(x)の符号が変化する
ことを示せばよいです。
上記1に関して、平均値の定理を使えば、f'(x)が定められた区間内に1つずつしか解を持たない事を示せます。上記2に関して、平均値の定理より、その区間内の解の前後でf'(x)の符号が反転しなければ、f(x)が単調増加また単調減少してしまい矛盾が発生します。よって「1と2と背理法」より証明終了となります。
受験生としての解説
2014年の九大数学5問で、1番難しい問題です。
大問4が中学生でも正解できるのに対し、大問5は九大合格者でもなかなか正解できないレベルです。「医学科の合否を分ける問題」とみなし、不正解でも構いません。九大数学は全5問から「2完答+3部分点」で非医歯薬系の合格得点率56%を作れるので、難しい問題は避け、簡単な問題を確実に拾ってください。
一方、大問1つの配点が50点と非常に大きいです。何か適当に書いて10%でも部分点を拾えれば、それだけで5点になります。これは九大英語なら
- 4択内容一致問題と同じ点数
- 4択語彙問題より1・2点高い点数
であり、他科目の「1問正解」に相当します。白紙で提出せず、何でもいいから書いてください。
- 上記1・2を示せば正解できる事は解ったが
- その方法が解らない
と採点者に伝わる答案(答案というより手紙)を作れば、正解できずとも部分点をもらえる場合があります。
- 計算:★★★(普通)
- 閃き:★★★★★(強く必要)
- 知識:★★★★(やや強く必要)
- 総合:★★★★★(難しい)
- 短評:医学科の合否を分ける問題
九州大学の数学2013年・平成25年度
大問1

講師としての解説
「積分」からの出題です。
計算量・難易度に関して、普通程度です。小問2でtanを自分で導入する計算があります。定番ですが少し難しいです。閃きの必要性に関して、少し必要です。基本的に「問題集のコピーの様な問題」ですが、計算過程で少し思考を要します。知識の必要性に関して、少ないです。定積分と三角関数ができれば十分です。
問1に関して、計算問題です。曲線と直線で囲まれた面積を答えます。台形から引き算すると楽に計算できます。問2に関して、極限値を求める問題です。2つの接線が作る角θは、2つの接線が「x軸と成す角」の足し算で表すことができます(θ=α+(-β)、βの値がマイナスなので)tanを使えばx座標・y座標だけで計算できる(斜めの要素を省ける)ので使ってください。最後にcosθの極限値を求めてtanθの極限値にかければ、正解の極限値asinθを得られます。
受験生としての解説
2013年の九大数学5問で、2番目に簡単な問題です。
九大数学は5つの大問から「2完答+3部分点」で非医歯薬系の合格得点率56%を作ることができます。そして、多くの年度で「完答しておきたい2問」の内1つは、大問1に来ています。2013年も(小問2が少し大変ですが)大問1は完答を目指したい1問です。大問1を完答し、残り4問から「1完答+3部分点」の状態を作れば、才能の無い学生さんでも安定して合格点を取ることができます。
- 計算:★★★(普通)
- 閃き:★★(やや少なめ)
- 知識:★(少ない)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問2

講師としての解説
「空間ベクトル」からの出題です。
計算量・難易度に関して、普通程度です。ベクトルの計算が続きますが、複雑にはなりません。閃きの必要性に関して、やや少ないです。ベクトル問題としては比較的簡単な部類です。知識の必要性に関して、やや少ないです。空間ベクトルの解法の定石を知っていれば、定石のまま正解できます。
誘導となる小問はありません。解き方の方向性を決めるため、手を動かす前に材料を確認するとベクトル問題は解きやすくなります。本問の場合
- 点Mと点Nは位置がハッキリしている
- 点Qは正解そのものと言えるので実数sを使って表す
- PQベクトル ⊥ OMベクトル
- PQベクトル ⊥ ONベクトル
- 問題文で内積値が2つ与えられている
という材料があります。これだけ材料があって、実質的に求めるのは点Qだけなので、それほど難しい問題ではないと解ります。具体的には、作図して考えずとも計算式を解くだけで正解できると予測が立ちます。予測が立ったら心に余裕を持ってスタートです。点Qは辺CB上にあるので、ある実数sを使ってsCBベクトルと表せます。「直線PQ⊥平面OMN」より
- PQ・OM=0
- PQ・ON=0
という2本の式が出てきます。未知の値は「実数s」と「PQベクトルの大きさ」の2つなので、「未知数2つ、式2本」の連立方程式を解いて正解となります。
受験生としての解説
2013年の九大数学5問で、1番目簡単な問題です
2013年は大問5「行列」が難しく、大問1~4が「標準~やや簡単」で似た難易度でした。その4問の中でも解きやすい・クセが無いのが本問です。完答を目指したい1問です。特に大問1で「tanの扱い」が解らず完答できなかった学生さんは、本問で挽回したいところです。大問1が完答できた学生さんは、もし本問も完答できれば合格得点率56%(2完答+3部分点)にほぼ届きます。簡単だからこそポイントと言える1問でした。
- 計算:★★★(普通)
- 閃き:★★(やや少なめ)
- 知識:★★(やや少ない)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問3

講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、簡単です。分数の計算だけです。閃きの必要性に関して、普通程度です。問題のシチュエーションを試験中に理解する必要があります。しかし、九大としては難しくない方です。知識の必要性に関して、ほぼ不要です。中学生でも正解できる問題です。
問1に関して、確率計算です。操作Lを2回行った後、コインの表が1枚になる確率を答えます。問題のシチュエーションがやや特殊なので、計算式を考えるより全パターン書き出した方が速く安全に正解できます。問2に関して、期待値を求める問題です。操作L→Rの順に操作した後、表になったコインの枚数の期待値を答えます。これも表を作って全パターン書き出せば、素早く安全に正解できます。問3に関して、操作L→R→Lの順に操作した後、全てのコインが表になる確率を答えます。問2で操作L→Rの状態を求めているので、活用してください。3回目の操作でコイン全部が表になれる状態だけをピックアップして場合分けすれば、素早く安全に正解できます。
受験生としての解説
2013年の九大数学で、3番めの難易度です。
計算せずとも、全パターン書き出せば中学生でも正解できる事を活用してください。2013年は、簡単な大問1・大問2を完答し、本問を全パターン書き出して完答すれば、非医歯薬系の合格得点率56%(2完答+3部分点)を作れます。合格するだけなら、難しい大問5に関わらなくて済むので、簡単な問題を確実に拾っていきましょう。
- 計算:★(簡単)
- 閃き:★★★(普通)
- 知識:★(ほぼ不要)
- 総合:★★(やや簡単)
- 短評:書き出せば誰でも正解できる
大問4

講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、普通程度です。回転体の体積問題としては式が少し複雑で、結果として積分計算も煩雑となります。しかし、量は多いですが難易度は普通です。閃きの必要性に関して、普通程度です。回転体の体積計算がやや複雑なので、それに対応する必要があります。知識の必要性に関して、やや少なめです。回転体の体積計算です。
問1に関して、円の中心座標と半径を求める問題です。中心の座標が与えられてないので自分で設定し、式を立てて解けば正解できます。円の中心が、原点と点Bを通る直線上にある事を利用すると、計算で少し楽をできます。問2に関して、回転体の体積計算です。回転軸がx軸でもy軸でもないため、まず平行移動させてx軸周りの回転体として考えます(平行移動させても体積は変化しない)後は円Sの回転体から円Tの回転体をくり抜く計算を地道に行えば正解できます。
受験生としての解説
2013年の九大数学5問で、2番目に難しい問題です。
例年の九大数学ですと「2番めに難しい問題」は、完答を意識せず部分点を狙います(2完答+3部分点で合格できるため)しかし、本問は九大で定番の「回転体の体積問題」であり、計算も複雑なだけで難しくないので、完答しておきたいレベルです。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★(やや少ない)
- 総合:★★★(普通)
- 短評:回転体の体積は九大の定番
大問5
講師としての解説
「行列」からの出題です。
現在は指導要領の範囲外なので、解説は割愛します。
受験生としての解説
2013年の九大数学5問で、1番難しい問題です。
2013年は大問1~4が「普通~やや簡単」で同程度なので、突出して難しい大問5は部分点を拾えれば十分です。
九州大学の数学2012年・平成24年度
大問1

講師としての解説
「積分」からの出題です。
計算量・難易度に関して、普通程度です。回転体の体積を積分計算します。円を回転させるため計算がやや煩雑になりますが、難しくはありません。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。知識の必要性に関して、やや少ないです。積分による回転体の体積計算ができれば十分です。
誘導となる小問はありません。問題の設定より
- 円の上側の部分を回転させた立体から
- 円の下側にできるスキマを回転させた立体を引けばよい
と解ります。円の上側・下側の式は、円の式を「y=」の形にすれば求まります。後は計算をすれば正解となります。途中のルートが絡む積分では「置換積分」しても構いませんし、図形的に「円の一部」と考えれば積分計算を省いて楽ができます。
受験生としての解説
2012年の九大数学5問で、1番簡単な問題です。
九大数学は全5問から「2完答+3部分点」で非医歯薬系の合格得点率56%に届きます。本問を完答しておけば、残り4問から「1完答+3部分点」で済むため合格が安定します。難しい問題を避け、簡単な問題を確実に正解しましょう。そうすれば才能が無い学生さんでも九大合格できます。
- 計算:★★★(普通)
- 閃き:★(ほぼ不要)
- 知識:★★(やや少ない)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問2
講師としての解説
「行列」からの出題です。
現在は指導要領の範囲外なので、解説は割愛します。
受験生としての解説
2012年の九大数学5問で、2番めに簡単な問題です。
大問3

講師としての解説
「解の存在条件」からの出題です。
計算量・難易度に関して、やや難しいです。問1の計算はやや煩雑であり、問2は自分で不等式を組み立てます。閃きの必要性に関して、やや強く必要です。絶対値に惑わされず定数分離に持ち込むことや、問2で自分で不等式を組み立てる部分などです。知識の必要性に関して、普通程度です。定数分離から解の存在条件に持ち込む流れを知っておく必要があります。
問1に関して、与式が実数解を持つようなaの範囲を求めます。a、x、nと3つの文字がありますが「nは自然数」なので「3や5と同じ」と気付いてください。実質、aとxの式なので、aを分離してxの塊をf(x)と置き、y=aのグラフとy=f(x)のグラフの「交点の条件」に持ち込めばよいです。しかし、素直に「a=」としてしまうと、絶対値が分母に来るため色々と気持ち悪いです(不完全解答で0点になる危険がある)そこで、絶対値が分子に来るよう「aを右辺」に分離し「√n/a」という形で定数分離します(nは自然数なので、この形でも定数分離できる)後は左辺をf(x)と置き、絶対値で場合分けして、f(x)を微分して増減表を書き、作図からグラフの交点に持ち込めば正解です。問2に関して、問1が全ての自然数nで成り立つようなaの値を求めます。「aの値の範囲」を定めている不等式左右のnに関し、「左右のnによる式が取りうる値」を各々求めれば、求めるべきaの範囲となります。
受験生としての解説
2012年の九大数学5問で、1番難しい問題です。
基本的に、九大数学で1番難しい問題は「医学科の合否を分ける問題」なので、非医歯薬系の受験生さんは正解できなくて構いません。特に、難問~超難問の場合は「大問丸ごと0点」でも大丈夫です。しかし、本問に関しては、小問2の不等式の組み立てでも「やや難しい」レベル、小問1なら「やや難しい~普通」レベルです。捨てるほど難しくありません。また、微積系(もしくは微積を使わない関数系)は九大数学の主軸なので、小問1は解けるようにしておきましょう。小問2は、模範解答を読んで理解できるレベルになっておきましょう。
そうすれば、九大数学5問中「簡単な2問」からの完答率が上がります。合格点(2完答+3部分点)を安定して作れるようになります。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:1番難しいが医学科専用という程ではない
大問4

講師としての解説
「数列」からの出題です。
計算量・難易度に関して、やや難しいです。数列の極限に関する計算が続きます。閃きの必要性に関して、普通程度です。最初から正解の形が見えにくいので、計算を進める中で気付いていく必要があります。知識の必要性に関して、やや強めに必要です。小問3の式変形において「β^2-β+1=0」から「β^2=β-1」として代入する(βが消えないのに、次数を下げるためだけにβを代入する)定石を知っておく必要があります。
問1に関して、証明問題です。a1、a2、a3が整数である事を示します。n=1,2,3と簡単なので、代入して計算を進めれば正解できます。解と係数の関係より、pとqの式に繋げれば良いです。問2に関して、証明問題です。「an+1/an」の極限値が整数である事を示します。分母分子を「αのn乗」と「βのn乗」で割ると極限値が求まります。問3に関して、条件を満たすp・qの値を全て求める問題です。問2の変形版で|α|・|β|の片方だけが「1より小」になります。問2より計算がやや煩雑ですが、考え方のベースは同じです。
受験生としての解説
2012年の九大数学5問で、2番めに難しい問題です。
1番難しい大問3と難易度は大差ないです。よって、両方から部分点を取りたいところです。小問1に関して、n=1・2・3を代入して計算するだけなのでこれは正解しておきましょう。小問2に関して、式の形がやや複雑ですが、分母分子を「αのn乗」と「βのn乗」で割るだけなので、九大対策の難関問題集より簡単です。ここまでは正解しておきたいところです。小問3に関して、「医学科専用」と言うほど難しくないですが、非医歯薬系の受験生さんは解けなくても構いません。九大数学は5つの大問から「2完答+3部分点」で合格できるので、本問は部分点を拾ってください
- 計算:★★★★(やや難しい)
- 閃き:★★★(普通)
- 知識:★★★★(やや強く必要)
- 総合:★★★★(やや難しい)
- 短評:難しいが医学科専用という程ではない
大問5
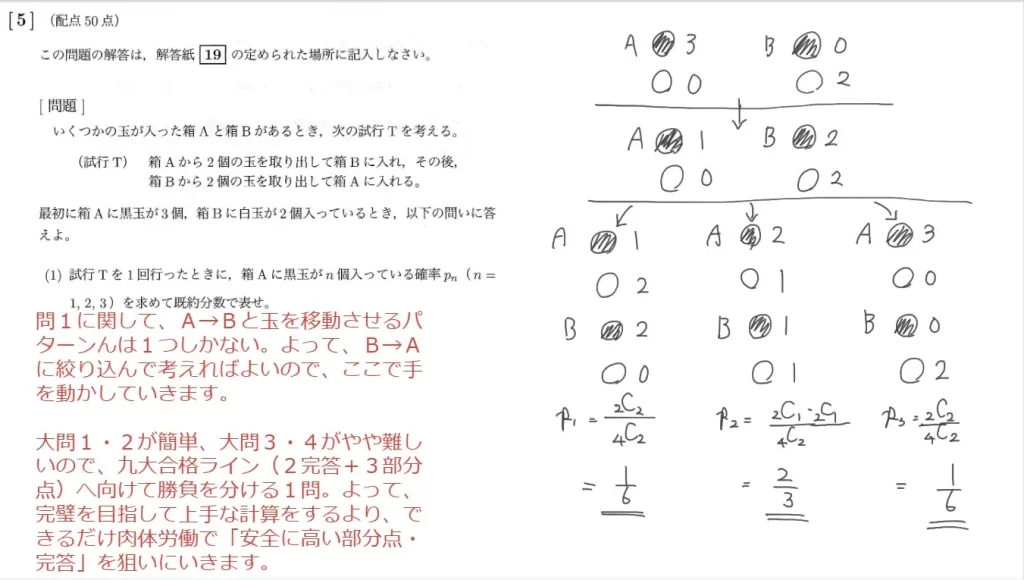
講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、簡単です。分数のかけ算で正解できます。閃きの必要性に関して、普通程度です。問題のシチュエーションに合わせて試験現場で考え、玉の出入りを書き出していきます。知識の必要性に関して、ほぼ不要です。中学生でも正解できます。
問1に関して、確率計算です。1回目の試行後に、箱Aに黒玉が入っている個数・確率を計算します。試行回数は1回・玉の移動パターンは3つしかないので、全パターン書き出せば安全に正解できます。問2に関して、確率計算です。2回目の試行後に、箱Aに黒玉が入っている個数・確率を計算します。問1より少し複雑ですが、箱に入る玉のパターンを書き出し、各々に関して確率計算すれば正解できます。問3に関して、確率計算です。3回目の試行後に、箱Aの中身が全て黒玉になっている確率を答えます。問2を応用すれば簡単に正解できます。よって、問2で玉の流れを丁寧に書き出しておく事が「完答のポイント」となります。
受験生としての解説
2012年の九大数学5問で、3番めの難易度です。
九大の「場合の数・確率」は頭で考えると難しいですが、手を使ってパターンを書き出せば、中学生でも正解できる問題がよくあります。これが3番めに難しいという事は、才能が無くても九大合格できるという事です。
九大数学は全5問から「2完答+3部分点」で、非医歯薬系の合格得点率56%に届きます。
計算:★(簡単)
閃き:★★★(普通)
知識:★(ほぼ不要)
総合:★★(やや簡単)
短評:中学生でも完答できる
九州大学の数学2011年・平成23年度
大問1

講師としての解説
「積分」からの出題です。
計算量・難易度に関して、やや簡単です。積分による面積計算ですが、最後まで簡単な数値が続きます。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。知識の必要性に関して、少なめです。積分による面積計算ができれば正解できます。
問1に関して、計算問題です。点Hの座標を求めます。グラフ上でy=xと直線PHは直交しているため、PHの傾きは-1と解ります。よって、直線PHの式を立て、y=xとの交点を求めれば正解です。問2に関して、計算問題です。y=x、直線PH、y=√xで囲まれた面積を答えます。点Hからx軸に垂線を下ろすと、√xの積分範囲で台形が2枚現れます。2枚の台形の面積から∫√xdxを引き算すると正解となります。問3に関して、計算問題です。y=√xとy=xで囲まれた面積が問2で求めた面積と等しくなる時の「tの値」を答えます。2つの面積を「=」でつなぐとtの二次方程式になります。それを解き、t>1の条件と照らし合わせると正解となります。
受験生としての解説
2011年の九大数学5問で、1番簡単な問題です。
小問1~小問3まで「問題集のコピーの様な問題」なことに加え難易度も簡単なので、全ての受験生さんが正解したい問題です。
九大数学は大問5つから「2完答+3部分点」で、非医歯薬系の合格得点率56%を作れます。本問を完答して残り「1完答+3部分点」の状態を作れば、才能の無い学生さんでも安定して合格点を取れます。
- 計算:★★(やや簡単)
- 閃き:★(ほぼ不要)
- 知識:★(少ない)
- 総合:★(簡単)
- 短評:完答したい1問
大問2

講師としての解説
「関数」からの出題です。
計算量・難易度に関して、普通程度です。微分して増減表を書き、大小関係と極限を調べます。閃きの必要性に関して、やや少なめです。小問3「極小値の位置」で場合分けが発生する際に少し思考を要します。知識の必要性に関して、やや少なめです。問題文の「3点で交わる」という文言から「y=kのグラフと3回交わる」と置き換えて考える定石を使います。
問1に関して、計算問題です。f(x)の極大値・極小値を答えます。微分して増減表をかけば正解できます。問2に関して、証明問題です。与えられた不等式が成り立つ事を証明します。「g(x)=右辺-左辺≧0」を示せば安全に正解できます。また「g(x)=左辺」と置いて単調減少から「左辺≦右辺」を示せばスマートな計算になります。証明した不等式をxで割って「はさみうちの原理」に持ち込めば、もう1つの設問である極限値も正解できます。問3に関して、与えられた2式のグラフが異なる3点で交わる条件を答えます。まず、2式からyを消去した式が「異なる3つの実数解」を持つ条件に帰着させます。次に、定数kを右辺に分離させ、左辺のグラフとy=kのグラフが3回交わる条件で考える定番の流れです。問2より、左辺の極限値(x→∞)は0なので、aの値によって(極小値がx軸より上か下かによって)場合分けが発生し、各々の条件で「グラフが3回交わる条件」を答えると正解となります。
受験生としての解説
2011年の九大数学5問で、3番めの難易度です。
小問1に関して、微分して増減表を書くだけなので、全ての受験生さんが正解したい問題です。小問2に関して、「はさみうちの原理」を使うとはいえ「合否を分ける問題」と言うほど難しくないので、落とすと痛い失点になります。全ての受験生さんが正解したい問題です。小問3に関して、合否を分ける1問です。グラフが3回交わるだけなら簡単な問題ですが「極小値の位置」で場合分けが発生しているため、普通程度の難しさになっています。
非医歯薬系の合格得点率56%(2完答+3部分点)の内、2完答を大問1・大問2で作れます。この2問の完答で九州大学へ合格できるならかなりお得です。完答を目指したい1問です。
- 計算:★★★(普通)
- 閃き:★★(やや少ない)
- 知識:★★(やや少ない)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問3

講師としての解説
「数列」からの出題です。
計算量・難易度に関して、普通程度です。量は少ないですが、式変形で一工夫あります。閃きの必要性に関して、普通程度です。小問3「an=tanθn」と自分で置いて考える部分で思考を要します。知識の必要性に関して、やや少なめです。数列の知識とtanθの公式で正解できます。
問1に関して、漸化式の一般項を求める問題です。与式を変形し一般項anを答えます。与式にn=1・2・3・・・と代入していくと「√3、-√3、√3、-√3・・・」の繰り返しと判り正解です。問2に関して、計算問題です「tanπ/12」の値を求めます。「π/12=π/3-π/4」と分割し、tanの引き算の公式に持ち込むと正解できます。本問から10年後、2021年九大数学・大問2(2)で全く同じ式変形を使います。問3に関して、与式を満たす最小の自然数kを求めます。問1の関係式に対し「an=tanθn」と置いてn=1・2・3・4・5・6・7・8・・・と代入していくと「4回ごとに同じ値」が繰り返されていると解ります。よって、問1と同じ要領でk=4が正解となります。
受験生としての解説
2011年の九大数学5問で、1番難しい問題です。
小問1に関して、n=1・2・3・・・と順に入れるだけなので、全ての受験生さんが正解したい問題です。小問2に関して、テクニカルな式変形ですが問題集を練習していれば同様の式変形は必ず見かけるので、落とすと痛い1問です。小問3に関して、難易度は普通ですが、九大としては珍しい形式で「頭の良い人ほど有利」な問題なので、不正解でも構いません。
才能で負けている学生さんは、頻出問題、基本問題、問題集のコピーの様な問題の3つで合格点を作っていきましょう。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★(やや少ない)
- 総合:★★★(普通)
- 短評:小問2まで正解したい
大問4

講師としての解説
「ベクトル」からの出題です。
計算量・難易度に関して、普通程度です。安全で不器用な解き方をした場合は「普通程度」で、上手な解き方をすれば「やや少ない」となります。閃きの必要性に関して、普通程度です。小問2において
- 平面ABCに垂直なベクトルnを仮定
- 点Fが三角形ABCの外心である事からの正弦定理
という2パターンの定石がありますが、いずれもやや思考力が必要です。知識の必要性に関して、普通程度です。空間ベクトルの定石を使うと正解できます。
問1に関して、計算問題です。4点O・A・B・Cを通る球の中心Dの座標を答えます。点Dの座標を(a,b,c)と仮定し、球の半径をrと仮定すると
- DOベクトルの大きさ=r
- DAベクトルの大きさ=r
- DBベクトルの大きさ=r
- DCベクトルの大きさ=r
と式が4本立ち「未知数4つ、式4本」で連立方程式を解くと正解できます。頭の良い人はもっと上手な解き方をしますが、九大に合格するだけなら安全で不器用な解法で十分です。問2に関して、計算問題です。点Dから平面ABCに下ろした「垂線の長さ」を答えます。
- 平面ABCに垂直なベクトルnを仮定し、内積を利用する解き方
- 点Fが三角形ABCの外心であることから、正弦定理を利用する解き方
などで正解できます。問3に関して、四面体ABCDの体積を求めます。問2でDFの長さ(四面体の高さ)を求めたので、底面(三角形ABC)の面積を計算すれば正解できます。
受験生としての解説
2011年の九大数学5問で、2番めに難しい問題です。
小問1に関して、連立方程式を解くだけなので、全ての受験生さんが正解したい問題です。小問2に関して、平面に垂線を下ろした時の定石を知っておく必要があり、合否を分ける1問です。小問3に関して、合否を分ける1問です。本問自体はやや簡単ですが、小問2の正解(DFの長さ)が無いと解けないため、小問2とセットで大きな配点となります。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:小問2が合否を分ける
大問5

講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、簡単です。分数のかけ算が中心です。閃きの必要性に関して、普通です。小問3までは少し必要で、小問4で一工夫あります。知識の必要性に関して、やや少ないです。C記号の計算、確率計算、期待値計算の知識が必要です。
問1に関して、確率計算です。2回の操作でカードが最初の配置に戻るのは「1回目と2回目に同じ球を引いた場合」です。問2に関して、確率計算です。球を2回引いて、カードの並びが4・3・2・1になるのは「1と4」と「2と3」の球が選ばれた場合です。問3に関して、確率計算です。2回の操作後に1のカードが左端にあるのは
- 1回目で1が移動し、2回目で1が左端に戻る
- 1が一度も移動しない
の2パターンです。問4に関して、期待値計算です。3回の操作後に「左端にあるカードの数の期待値」を答えます。問1~問3を通して「1のカードに関する確率」を調べてきました。よって、確率100%からそれを引くと「2・3・4のカードの確率」が求まります。2・3・4のカードには「対称性」があり、確率は均等なので「1を除いた確率÷3」で2・3・4の確率が求まります。後は期待値計算で正解です。
受験生としての解説
2011年の九大数学5問で、2番めに簡単な問題です。
小問1~小問3に関して、簡単な確率計算なので、全ての受験生さんが正解したい問題です。小問4に関して、合否を分ける1問です。余事象とカード2・3・4の対称性に気づけば正解できます。しかし、仮に解けないとしても、球の引き方(=カードの移動パターン)は最終問題ですら216通りしかないので、全パターン書き出せば正解できます。
- 計算:★(簡単)
- 閃き:★★★(普通)
- 知識:★★(やや少ない)
- 総合:★★(やや簡単)
- 短評:完答したい1問
九州大学の数学2010年・平成22年度
大問1

講師としての解説
「図形と計量」からの出題です。
計算量・難易度に関して、やや簡単です。基本的に余弦定理の式を解く程度です。小問3における不等式の使い方が少し難しいです。閃きの必要性に関して、普通程度です。小問2までは簡単ですが、小問3が思考を要する問題です。知識の必要性に関して、やや少ないです。余弦定理の知識で解けます。
問1に関して、CPの2乗の長さを答える問題です。与えられた情報が「辺の長さ」しかないので、余弦定理を使うだろうと想像できます。2枚の三角形は∠Aを共有しているので、2枚の三角形に対して余弦定理で∠Aを表し、イコールでつないで解けば正解となります。問2に関して、CP=aなる時のtの値を答える問題です。問1の計算結果に「CP=a」を代入すると正解できます。t≧0に注意してください。問3に関して、∠Aと∠Bの関係を答える問題です。問題文が「∠Aと∠Bに関する条件を求めよ」という曖昧な表現なので、不等式を立てて関係性をハッキリさせれば正解できます。不等式を立てる際には問2を応用してください。問2において、tが2つある方の「b≧a」という関係が正解のベースとなります。
受験生としての解説
2010年の九大数学5問で、3番めの難易度です。
九大数学では全5問中「1番簡単な問題」が大問1に来る場合が多く、本問も小問2までなら「1番簡単」と感じる難易度です。しかし、小問3の不等式の変形で「普通程度」の難易度に上がるため、解けなくて焦らないよう注意してください。2010年の簡単な問題は、大問2と大問4です。
九大数学は全5問から「2完答+3部分点」で、非医歯薬系の合格得点率56%を作れます。難しい問題は避け、簡単な問題を確実に拾えば、才能の無い学生さんでも九大合格できます。
- 計算:★★(やや簡単)
- 閃き:★★★(普通)
- 知識:★★(やや少ない)
- 総合:★★(やや簡単)
- 短評:小問3で難度が上がる
大問2

講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、簡単です。分数のかけ算で正解できます。閃きの必要性に関して、普通程度です。問題のシチュエーションを試験中に理解し、解答方法を自分で決めます。知識の必要性に関して、ほぼ不要です。中学生でも正解できます。
問1に関して、期待値計算です。サイコロを2回振った時の得点期待値を答えます。難しい計算をせずとも、全パターン書き出せば素早く安全に正解できます。問2に関して、期待値計算です。1投目に6が出た時は、2投目を放棄した方が期待値が上がります。その値を答えます。本問も計算するより全パターン書き出した方が素早く安全に正解できます。問3に関して、期待値計算です。競技者にとって最も得になる2投目の振り方を答えます。最初の目をkとして期待値の式を立てればキレイに解答できます。それが難しい人は全パターン書き出し、競技者が損しないギリギリの目を答えれば正解となります。
受験生としての解説
2010年の九大数学5問で、1番簡単な問題です。
最後の小問3までサイコロを振る回数は2回のままなので、出目の全パターンは36通りです。難しい計算式を立てずとも、全て書き出せば安全に正解できます。完答を目指したい1問です。
- 計算:★(簡単)
- 閃き:★★★(普通)
- 知識:★(少ない)
- 総合:★★(やや簡単)
- 短評:書き出せば中学生でも正解できる
大問3

講師としての解説
「微分」と「数列」からの出題です。
計算量・難易度に関して、普通程度です。2本の曲線に対し接線と交点を繰り返し計算し、漸化式に持ち込みます。閃きの必要性に関して、やや少ないです。問題は複雑ですが、解き方は基本的に1本道です。知識の必要性に関して、普通程度です。微分、接線、漸化式、シグマ記号など普通の事が普通にできれば大丈夫です。
問1に関して、接線との交点の座標を求める問題です。x=tにおける接線の方程式を立て、曲線の式と連立すれば正解できます。問2に関して、三角形の面積を求めます。角頂点はP1,Q1,P2であり具体的に求められる点なので難しくはないでしょう。ベクトル要素による「三角形の面積の公式」を導けるようにしておきましょう。問3に関して、三角形の面積を求めます。角頂点はPn,Qn,Pn+1で一般化されています。点Pnのx座標を「x=an」と置けば、問2と同じです。問4に関して、シグマ記号による級数計算です。等比数列の和の公式を導けるようにしておけば正解できます。
受験生としての解説
2010年の九大数学5問で、2番目に難しい問題です。
問題の設定がやや複雑ですが「x=an」と置いて漸化式に持ち込む事さえ気づけば、ほぼ1本道の問題です。才能が無くても正解できるタイプの問題なので、才能が無い学生さんほど完答したい問題です。
全パターン書き出せば正解できる大問2と本問を完答すれば、残りは「0完答+3部分点」で非医歯薬系の合格得点率56%を作れます。
- 計算:★★★(普通)
- 閃き:★★(やや少ない)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:やや複雑だが考える事は少ない
大問4

講師としての解説
「いろいろな曲線」からの出題です。
計算量・難易度に関して、普通程度です。曲線の長さに関する積分計算があります。閃きの必要性に関して、普通程度です。問1では移動する円の周上を動く点をベクトルで表示します。問2ではtの事を一旦忘れ「yをx方向に積分している」と気づく必要があります。知識の必要性に関して、普通程度です。「曲線の長さに関する積分」は基本ではありますが、常に使い続けるものでもないため、少し難しいです。
問1に関して、計算問題です。点Pの座標を求めます。点Pは円上を周回する点ですが、円自体が右向きに移動しているため複雑な動きとなっています。この様な点を表すのに便利な道具がベクトルです。
- 円の中心へ向かうOQベクトル
- 円の中心から点Pへ向かうQPベクトル
と分割して考えることで簡単に点Pの座標を表示できます。問2に関して、点Pの描く軌跡とx軸がなす部分の面積を求めます。点Pがパラメタtで表示されている事が難しさのポイントです。一旦tの事を忘れ、何を求められているか考えてみてください。「点Pのy座標をx軸方向に積分する問題」である事を思い出せば、後は媒介変数tによる積分計算をするだけで正解できます。問3に関して、計算問題です。曲線Cの長さを求めます。曲線を求める積分公式を使うわけですが、丸暗記で済ませている学生さんは忘れやすい部分です。丸暗記せず、理屈を理解しておけば簡単な問題となります。
受験生としての解説
2010年の九大数学5問で、2番めに簡単な問題です。
- 転がる円の上を周る点
- その点が作る軌跡
- 曲線の長さ
と3種類の基礎を問われる出題でしたが、逆に言えば、練習しておけば練習そのままの問題です。最後の小問3ですら「曲線の公式」そのままで正解できます。よって本問は完答しておきたい1問となります。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:基本の集合体
大問5
講師としての解説
「行列」からの出題です。
現在は指導要領の範囲外なので、解説は割愛します。
受験生としての解説
2010年の九大数学5問で、1番難しい問題です。
九州大学の数学2009年・平成21年度
大問1

講師としての解説
「ベクトル」からの出題です。
計算量・難易度に関して、やや簡単です。平方完成で最小値を求めます。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。そして問題集より簡単です。知識の必要性に関して、少ないです。二次関数の最小値を「軸の位置」で場合分けする程度です。
問1に関して、計算問題です。「CPベクトルの2乗」を求めます。直線ACの方程式を求め、直交条件から直線OCの方程式を導き、点Cの座標を確定させます。CPベクトル=OPベクトル-OCベクトルより正解できます。問2に関して、計算問題です。問1で求めた「CPベクトルの2乗」の最小値を答えます。条件よりsは定数扱いできるので、tの二次関数と見なします。グラフは下向きに凸なので、平方完成より最小値が求まります。軸の位置によって最小値を2通りに場合分けすれば正解となります。
受験生としての解説
2009年の九大数学5問で、1番簡単な問題です。
平方完成による最小値を求めるだけの問題なので、完答を目指したい1問です。九大数学は全5問から「2完答+3部分点」で非医歯薬系の合格得点率56%に届きます。2完答の内1つを本問で達成しておけば、残り4問から「1完答+3部分点」で済むため合格が安定します。
- 計算:★★(やや簡単)
- 閃き:★(ほぼ不要)
- 知識:★(少ない)
- 総合:★(簡単)
- 短評:完答したい1問
大問2

講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、普通程度です。偶数・奇数に場合分けしながら確率計算についての漸化式を立てます。閃きの必要性に関して、強く必要です。複雑なシチュエーションを理解しつつ、それを数列の計算に落とし込み、偶数と奇数で場合分けしながら解答を進める必要があります。知識の必要性に関して、普通程度です。漸化式、シグマ記号、偶数・奇数の表し方などの定石を使います。
問1に関して、確率計算です。カード操作を1回・2回行った時に、カードの合計値が偶数になる確率を答えます。問題のシチュエーションを理解させるための誘導問題ですが、既に少し難しいです。2回目終了時に2枚のカードの和が偶数になるのは、連続で奇数・偶数を引いた時なので、それを数式で表すと正解できます。問2に関して、漸化式を立てる問題です。n回目とn+1回目の操作間にある関係を漸化式で答えます。n回目終了時にカードの和が偶数・奇数の2パターンに分かれるため、各々について確率計算し足し合わせれば正解となります。問3に関して、「M-N/M+N」をkで置き換える問題です。ここまでは偶数をM・奇数をNで表してきましたが、偶数・奇数を両方兼ねるkを使って表します。偶数は「k=2m」奇数は「k=2m+1」と表せるため、これを使って計算を進め、M・Nに置き換えると正解となります。問4に関して、pnをnとkで表す問題です。問1~問3を応用し、確率の式を一般化して終了となります。
受験生としての解説
2009年の九大数学5問で、2番目に難しい問題です。
本問の難しさは、偶数・奇数の両方を兼ねる「k」にあります。よって、kが出てこない小問2までは普通の問題なので正解したいところです。逆にkが出てくる小問3以降は「医学科の合否を分ける問題」とみなし、切り捨てても構いません。
- 計算:★★★(普通)
- 閃き:★★★★★(強く必要)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:小問2まで正解したい
大問3

講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、やや難しいです。見た目は簡単ですが「a=0の可能性」が出たり「xの2/3乗をtで置換」したり煩雑です。閃きの必要性に関して、やや少なめです。積分計算による面積計算を目指す定番の流れです。知識の必要性に関して、普通程度です。直交条件、軌跡の表示、面積計算、普通の事を一通り求められます。
問1に関して、点Aの座標を求める問題です。x=aからの法線を求める際に、計算過程でaが分母に来ます。よって「a=0」の確認を注意してください。交点の座標と極限値の計算は難しくありません。問2に関して、曲線C1・C2の交点を求める問題です。問1でC2の座標が解ったので、そこから軌跡を求め、軌跡がC1と交わる点を求めます。点Aのx・y座標はaを媒介して表示されているで、x・yの式からaを消去すれば正解できます。途中「xの2/3乗」が出てきて計算が複雑になりますが、tと置き換えると楽になります。問3に関して、面積計算です。問2で「C1・C2の交点」が求まったので、挟まれた区間の面積を答えます。本問はただ積分計算をするだけで、問2が解けた人へのボーナス点の様な問題です。
受験生としての解説
2009年の九大数学5問で、3番めの難易度です。
計算が煩雑で完答までに疲れる問題ですが、やっている事は普通です。私立中学的な図形は無いし、医学部的な式変形もありません。楽して解ける問題ではありませんが、特別な事は必要ないので、才能の無い学生さんはこの様な問題を確実に正解できるよう準備してください。努力すれば誰でも解けるようになる問題です。
- 計算:★★★★(やや難しい)
- 閃き:★★(やや少なめ)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:才能が無い人ほど重視したい1問
大問4
「行列」からの出題です。
現在は指導要領の範囲外なので、解説は割愛します。
大問5

講師としての解説
「微分」からの出題です。
計算量・難易度に関して、普通程度です。速度ベクトル・加速度ベクトルに関する計算が続きます。閃きの必要性に関して、やや少なめです。問題集のコピーの様な問題です。知識の必要性に関して、やや強めに必要です。「速度ベクトル・加速度ベクトル」という練習で手が届きにくい分野からの出題です。ただ、問題集に必ず載っているレベルなので、訓練しておけば比較的楽に解ける問題でもあります。
問1に関して、速度ベクトルを答える問題です。ゴールは(dx/dt,dy/dt)なので、x要素・y要素ごと別々に丁寧に計算していけば正解できます。問2に関して、加速度ベクトルαを答える問題です。問1で「速度ベクトル」を求めたので、それを時間tでもう1度微分すると求まります。記号が複雑で混乱しそうな場合は「dx/dt=X」「dy/dt=Y」と置き換えると解りやすくなります。問3に関して、加速度ベクトルの大きさの最大値を答える問題です。問2で「加速度ベクトル」を求めたので、これをsの関数とみなし最大値を求めます。最大値以外は求めなくてよいので、計算を複雑にしている「eの2s乗」は簡単な文字に置き換えて考えれば良いです。
受験生としての解説
2009年の九大数学5問で、2番めに簡単な問題です。
速度ベクトルは、数学Ⅲの中でも勉強が行き届きにくい分野です。問題自体はやや簡単なのですが、知識不足の状態で正解を出せるレベルでもないため、怖い出題でした。逆に言えば、才能が無くてもキチンと勉強しておけば合格点を取れる1問です。
- 計算:★★★(普通)
- 閃き:★★(やや少なめ)
- 知識:★★★★(やや難しい)
- 総合:★★★(普通)
- 短評:落とすと痛い1問
九州大学の数学2008年・平成20年度
大問1

講師としての解説
「微分」からの出題です。
計算量・難易度に関して、普通程度です。2回微分からの増減表、逆関数、不等式の運用があります。閃きの必要性に関して、少し必要です。問題集のコピーの様な問題です。知識の必要性に関して、やや少なめです。上記計算に関する基本知識が必要です。
問1に関して、計算問題です。2回微分して増減表を書き、極限を調べ、グラフを描けば正解です。問2に関して、逆関数を答える問題です。与式を変形して「x=」の形を作り、xとyを入れ替えれば正解できます。問3に関して、逆関数の極限値を求めます。問2で求めた逆関数に問3の値を代入して計算すれば正解できます。最後に「極限の公式」が必要になるので憶えておきましょう。
受験生としての解説
2008年の九大数学5問で、1番簡単な問題です。
微分して、増減表を書いて、作図して、逆関数を求めれば正解ということで、才能が無い学生さんでも訓練すれば必ずできるようになります。
九大数学は大問5つから「2完答+3部分点」で非医歯薬系の合格得点率56%を作れます。5問の内1・2問は本問の様な「訓練しておけば必ず正解できる大問」が毎年含まれているので、そこから「2完答の内1つでも」稼げば、残り4問「1完答+3部分点」の状態にできます。難しい問題は避け、簡単な問題から合格点を確実に拾ってください。
- 計算:★★★(普通)
- 閃き:★★(少し必要)
- 知識:★★(やや少ない)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問2

講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、普通程度です。確率計算・シグマ記号の計算があります。閃きの必要性に関して、普通程度です。問題のシチュエーションがやや複雑なので、それに合わせた立式で思考力を使います。知識の必要性に関して、ほぼ不要です。シグマ記号の計算ぐらいです。
問1に関して、確率計算です。1点・10点という極端な数値を使うことで、受験生さんにシチュエーションを理解させる問題です。問2に関して、確率計算です。問1の得点を「n点」と一般化する問題です。kより大きい得点・k以下の得点の2パターンでカードの引き方が変わるため、確率の式が変化します。問3に関して、期待値計算です。問2で「得点の一般化」を行ったので、期待値を計算してシグマ記号で集めよう、という問題です。このタイプの計算問題としては、やや簡単な部類です。
受験生としての解説
2008年の九大数学5問で、2番めに簡単な問題です。
小問1に関して、具体的な数値で計算できるため、全ての受験生さんが正解したい問題です。小問2に関して、数値が一般化(n化)して難易度が上がっていますが「確率計算の一般化」としては、出てくる数式がシンプルなので、落とせない問題です。場合分けもあって大変なのですが、ここは乗り越えたいところです。小問3に関して、小問2が解けた人ならセットで正解できるでしょう。
本問が解けなかった場合は、3番めに簡単な大問4の完答を目指してください。本問「場合の数・確率」は分野を苦手とする学生さんが多く、問題のシチュエーションを試験現場で理解しないといけないため、完答確率が不安定になりやすいですが、大問4「微分積分」は逆に安定性の高い分野です。
大問1・大問2を完答しておけば、残り3問から「0完答+3部分点」で非医歯薬系の合格得点率56%を作れます。難しい問題は避け、簡単な問題を確実に拾ってください。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★(ほぼ不要)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問3

講師としての解説
「平面ベクトル」からの出題です。
計算量・難易度に関して、やや簡単です。計算は少ないですが、三角形OABを「a+b-c」と表す事に気づく部分がやや難しいです。閃きの必要性に関して、普通程度です。小問3のシチュエーションを受け入れ、作図に持ち込む部分で少し思考を要します。知識の必要性に関して、やや少なめです。1辺を共有した三角形の面積比を扱えれば十分です。
問1に関して、OQベクトルを求める問題です。⊿OAPと⊿OBPは辺OPを共有しているので、AQ:BQがそのまま三角形の面積比になっています。それを知らない場合は、点A・点Bから辺OPに垂線を下ろせば見えてきます。問2に関して、OPベクトルを求める問題です。ポイントは⊿OABの面積を「a+b-c」で表せる事です。これが見えれば問1と同じ方法で、OQ:PQが⊿OABと⊿ABPの面積比に等しい事から正解が求まります。問3に関して、シチュエーションを変えてOPベクトルを求める問題です。突然出てきた円ですが、このシチュエーションでは
- 中心と接点を結ぶ角が90°になる
- 中心から全ての接点までの長さが半径rになる
ぐらいしか使い道が無いので、逆に言えば、これを使って正解に導くと解ります。そうすると「中心→接点」の線分が「三角形の高さ」になっている事が見え、正解となります。
受験生としての解説
2008年の九大数学5問で、2番めに難しい問題です。
小問1は全受験生さんが正解したい問題です。小問2は「⊿OAB=a+b-c」と気付けるかが勝負どころです。小問3は九大受験生なら正解したいレベルですが、2008年は他にも得点源がたくさんあるので、不正解でも構いません。
簡単な大問1・大問2を完答し、本問と大問4から半分ほど部分点を拾っておけば、仮に難しい大問5が0点でも非医歯薬系の合格得点率56%に届きます。
- 計算:★★(やや簡単)
- 閃き:★★★(普通)
- 知識:★★(やや少なめ)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問4
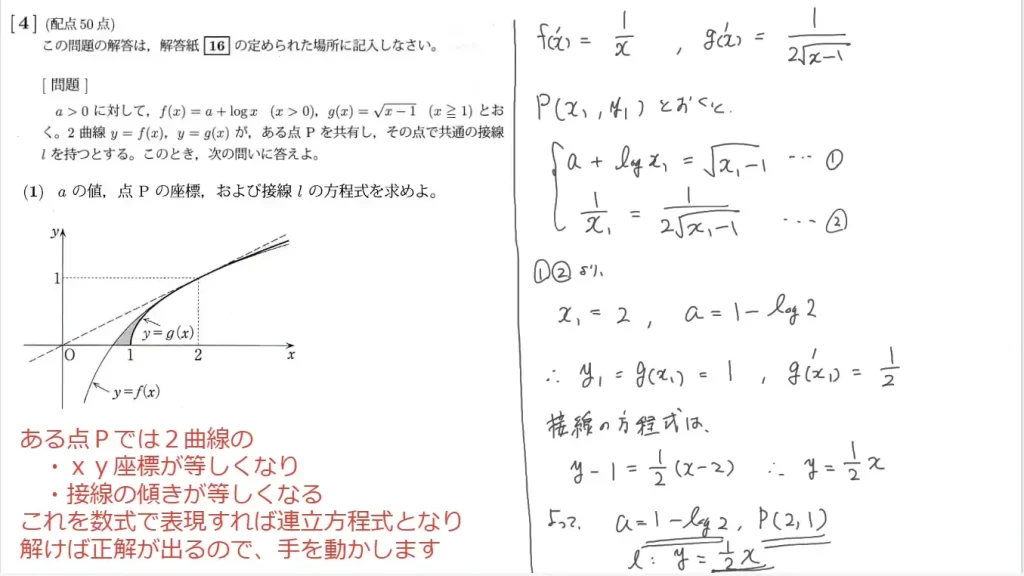
講師としての解説
「積分」からの出題です。
計算量・難易度に関して、普通程度です。微分して増減表を作り積分計算しますが、与えられる式はやや簡単です。閃きの必要性に関して、やや少なめです。問題集のコピーの様な問題です。知識の必要性に関して、やや少なめです。ルートの微分、増減表、積分の基本レベルを問われています。
問1に関して、計算問題です。aの値、Pの座標、直線lの式、と一気に問われていますが「芋づる式」に解けるので難しくありません。問題文から使えそうな条件は「点Pを共有し、点Pで共通の接線を持つ」だけなので、この2つを数式にしてください。連立方程式を解けば正解です。問2に関して、証明問題です。2曲線が点P以外は共有点を持たない事を示します。2曲線の式を引き算した関数を作り、その関数のグラフが「x軸と1回しか交わらない」ことに落とし込めば正解できます。つまり、微分して、増減表を書いて、単調減少を示すだけです。問3に関して、面積計算です。問2の結果で「y=f(x)とy=g(x)の上下関係」がハッキリしたので、積分計算して完答となります。
受験生としての解説
2008年の九大数学5問で、3番めの難易度です。
大問2「場合の数・確率」が苦手で完答できなかった場合は、本問から完答を目指してください。問題集のコピーの様な問題なので、大問1・大問2より簡単だと感じる学生さんも多いと思います。
- 計算:★★★(普通)
- 閃き:★★(やや少なめ)
- 知識:★★(やや少なめ)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問5

講師としての解説
「三角関数」からの出題です。
計算量・難易度に関して、普通程度です。三角関数の基本的な計算が続きます。自分で不等式を設定する部分がやや難しいです。閃きの必要性に関して、やや強めに必要です。小問3で「角θが2πを超えない個数=円を配置できる個数」と気づく必要があります。知識の必要性に関して、普通程度です。図形と三角関数の基本知識で解けます。
問1に関して、sinθの値を求める問題です。与えられた条件を作図し、図中のθを使います。ポイントは、円Qと円Rの中心を結ぶことです。直角三角形が発生するのでsinθ/2の計算に持ち込めます。三角関数の公式でsinθに戻すと正解です。問2に関して、証明問題です。「π/3<θ<π/2」を証明します。問1で「sinθ/2=3/5」と値を出しているので、これを利用して自分で不等式を設定します。「sinπ/6<3/5<sinπ/4」なので「π/6<θ/2<π/4」となり、全体を2倍すれば証明完了となります。問3に関して、円Rの周囲に配置できる円Qの個数を求めます。問1・問2を活用し「θを足していき、2π(360°)をギリギリ超えない個数が求める円の個数」と気付ければ正解できます。
受験生としての解説
2008年の九大数学5問で、1番難しい問題です。
小問1は、全受験生さんが正解しておきたいレベル。小問2は、自分で不等式を設定する問題としては簡単な部類なので、九大受験生なら解けてほしいレベルです。しかし、2008年は本問を正解できなくても非医歯薬系の合格得点率56%を作れるので、不正解でも構いません。小問3は「医学科限定」というほど難しくありませんが、難問なので医学科・臨床科以外の受験生さんは解けなくて構いません。
- 大問1~大問4から確実に合格点を作ること
- 英語・物理・化学の簡単な問題を確実に正解できること
の方が大切です。
- 計算:★★★(普通)
- 閃き:★★★★(やや難しい)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:小問2まで正解したい
九州大学の数学2007年・平成19年度
大問1

講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、やや簡単です。積分による面積計算ですが、値は簡単なものだけです。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。知識の必要性に関して、やや少なめです。増減表、作図、面積計算で十分です。
問1に関して、証明問題です。「f(x)-g(x)≧0」の証明ということで、左辺をh(x)と置いて「h(x)の最小値≧0」に持ち込めば正解できます。問2に関して、面積Sの最小値を与えるx=pを求める問題です。積分計算で面積Sを求めた後、Sを「pの関数」とみなし微分して増減表を書けば正解できます。
受験生としての解説
2007年の九大数学5問で、1番簡単な問題です。
問1・問2ともに全ての受験生さんが正解しておきたいレベルです。
本問が解けない場合は、大問2・大問4からの完答を目指してください。特に大問4「場合の数・確率」は、時間をかければ必ず正解に行き着くタイプなので、試験時間を回す価値があります。
九大数学は全5問から「2完答+3部分点」で非医歯薬系の合格得点率56%を作れます。難しい問題は避け、簡単な問題を確実に正解すれば、才能が無い学生さんでも九大合格できます。
- 計算:★★(やや簡単)
- 閃き:★(ほぼ不要)
- 知識:★★(やや少ない)
- 総合:★(簡単)
- 短評:完答したい1問
大問2
「行列」からの出題です。
現在は指導要領の範囲外なので、解説は割愛します。
大問3

講師としての解説
「空間ベクトル」からの出題です。
計算量・難易度に関して、やや簡単です。三角形の面積や内積などベクトルの計算ですが、値は簡単です。閃きの必要性に関して、やや強めに必要です。点A・B・Cを通る平面と球が同時に登場するため、適応する必要があります。知識の必要性に関して、普通程度です。ベクトルにおける平面と球の扱い方を知っておく必要があります。
問1に関して、証明問題と面積計算です。まず「垂直の証明」ですが、ベクトルで垂直と言えば「内積=0」です。内積はDC、DO、ABベクトルの要素をかけて足せば0になります。次に「面積計算」ですが、点Dが線分ABの中点かつDC⊥ADなので「線分DCが三角形の高さ」になっていると気づけば正解です。問2に関して、線分OHの長さを求めます。DCベクトルとDOベクトルはxyz要素が明らかなので「内積」の値が解ります。つまり「なす角」をθと置くとcosθの値が求まります。cosθが解ればsinθの値も求まり「OH=ODsinθ」なので正解となります。問3に関して、四面体ABCPの体積の最大値を求めます。ポイントは「点Pの位置」で、HOを真っすぐ伸ばした球との交点がPの時、四面体の高さが最大(体積が最大)となります。HOは問2で求めており、OPは球の半径なので、体積はすぐ計算でき正解となります。
受験生としての解説
2007年の九大数学5問で、2番めに難しい問題です。
小問1は「内積=0」と「三角形=底辺×高さ×1/2」なので、全受験生さんが正解したい問題です。小問2は簡単ではありませんが、問題集のコピーの様な問題なので合否を分ける1問です。小問3は九大の標準レベルという問題ですが、2007年は大問1・大問2・大問4が簡単なので、不正解でも構いません。
「2完答+3部分点」で非医歯薬系の合格得点率56%に届くので、難しい問題は避け、簡単な問題を確実に拾えば、才能の無い学生さんでも九大合格できます。
- 計算:★★(やや簡単)
- 閃き:★★★★(やや強く必要)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:小問2まで正解したい
大問4

講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、普通程度です。場合の数を「総当りで確認」れば安全に正解できるので、肉体労働してください。閃きの必要性に関して、やや少なめです。総当たりで表を作った方が簡単だと気づく部分で閃きが必要です。知識の必要性に関して、ほぼ不要です。判別式を知っていれば中学生でも正解できます。
問1に関して、場合の数を求める問題です。与式が実数解を持つ積acの値を調べ、(a,c)の取りうる値の個数を調べます。実数解という事で「判別式=b^2-4ac」を書くと問題文の「ac」が姿を表します。サイコロbの値1~6で6パターンに場合分けし、各々に「ac」の正解を調べていけば素早く安全に正解できます。問2に関して、確率計算です。与式が「有理数の解」を持つ確率を答えます。つまり「解の公式」における「b^2-4ac」が平方数となり「ルートが消える」ことが条件となります。要するに「何か2乗になればよい」ので、問1同様、サイコロbの出目1~6パターンに分けて、各々「acの値」を検証すれば正解できます。
受験生としての解説
2007年の九大数学5問で、2番めに簡単な問題です。
小問1・小問2ともに、全ての受験生さんが正解したい問題です。全パターンを書き出すだけで大問1つ完答できるので、才能の無い学生さんほど大事にしたい1問です。こういう問題を確実に拾って「2完答+3部分点」を作れば九大合格できます。
本問が解けない場合は、1番簡単な大問1を完答し、本問と差が無い大問2の完答を目指してください。そして大問3で多めに部分点を取って得点率56%とし、英語・物理・化学に負担を回さないようにしたいところです。
- 計算:★★★(普通)
- 閃き:★★(やや少なめ)
- 知識:★(ほぼ不要)
- 総合:★(簡単)
- 短評:完答したい1問
大問5

講師としての解説
「三角関数」からの出題です。
計算量・難易度に関して、やや難しいです。絶対値・必要十分条件・三角関数の周期などを使い、自分で立式して解答を進めていきます。閃きの必要性に関して、やや強めに必要です。問題文で提示されたルールを理解して受け入れ、その場で応用していくタイプです。知識の必要性に関して、やや強めに必要です。三角関数の周期を中心に、絶対値・必要十分条件・整数などを柔軟に使える必要があります。
問1に関して、関数|sinx|の基本周期を答える問題です。「基本周期の定義」が問題文で与えられているので、まず理解してください。与式は恒等式なので「x=0」の時も成り立ちます。よって、x=0を代入し出てきたp=πが正解となります。この時点では「必要条件」でしかないため、折返し「p=π」で与式を計算し「十分条件」である事も確認すれば正解となります。問2に関して、pがf(x)の周期ならばf(π/2)=-f(π/2)=0である事を示します。問1で使った「周期関数の定義」は問2でも使えるので「x=-π/2」を代入すると、示すべき式の形となり正解できます。問2はもう1つ問題があり「mpがπの整数倍であり、npが2πの整数倍である」事を示します。k・lを整数として「mp/2=kπ」「mp/2=lπ」と置いて計算を進めると正解できます。問3に関して、問2の結果を使って「|sinmx|sinnxの基本周期」を求めます。問2の結果より「mp=2k’π」「np=2l’π」とできるので、2式からpを消去して「nk’=2ml’」と書き換え、m・nが互いに素である事を利用して計算を進めていくと正解できます。
受験生としての解説
2007年の九大数学5問で、1番難しい問題です。
小問1は、九州大学を目指すなら解けてほしいレベルです。しかし「落とすと痛い失点」という簡単さではなく(むしろ小問1から難しいです)また2007年の大問1~4の簡単さを考えれば、不正解でも構いません。小問1を正解するより、大問1・大問4を完答する方が楽です。よって、更に難易度が上がる小問2・小問3は「医学科の合否を分ける問題」とみなし、不正解で構いません。
白紙で提出せず、どんなツマラナイ事でも良いので書いてください。配点が50点もあるので、10%でも正解にかすれば部分点が5点も入ります。これは英語・物理・化学の「4択問題から1問正解」の価値があります。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや強めに必要)
- 知識:★★★★(やや多く必要)
- 総合:★★★★★(難しい)
- 短評:医学科の合否を分ける1問
九州大学の数学2006年・平成18年度
大問1

講師としての解説
「曲線のグラフ」からの出題です。
計算量・難易度に関して、普通程度です。小問2で不等式を設定して「はさみうちの原理」に持ち込む部分が少し難しいです。閃きの必要性に関して、普通程度です。小問2が普通程度に難しいです。知識の必要性に関して、普通程度です。はさみうちの原理に持ち込む流れを知っておく必要があります。
問1に関して、証明問題です。与式がx>0の範囲で「2つの実数解」を持つ事を示します。右辺が定数分離の形になっているので、左辺をf(x)と置いて微分・増減表から作図します。そして、右辺のグラフとの交点を確認すれば正解できます。問題集のコピーの様な問題です。問2に関して、証明問題です。与えられた不等式が成り立つ事を証明し、anの極限値を求めます。問1の与式を左辺に集めたものをg(x)と置き、y=g(x)のグラフが「最初の不等式」のxの範囲内で
- 左端<0
- 単調増加
- 右端>0
である事を示せば、最初の不等式は証明完了です。反対に2番めの不等式では、その範囲内において
- 左端>0
- 単調減少
- g(x)の極限値<0
である事を示せば証明完了となります。最後に「はさみうちの原理」よりanの極限値が求まって終了です。
受験生としての解説
2006年の九大数学5問で、2番めに簡単な問題です。
小問1は「問題集のコピーの様な問題」なので、全ての受験生さんが正解したいところです。小問2も問題集のコピーの様な問題ではありますが「中間値の定理」と「はさみうちの原理」を使いこなす事は、コピー問題であっても少し難しいです。
そこで「数学5問全体」から考えてみましょう。本問は「2番めに簡単な大問」なので、九大非医歯薬系の合格得点率56%(2完答+3部分点)に届かせるためには、完答しておきたい1問と解ります。少し大変ですが、九大の標準レベルなので、本問が完答できるよう準備してください。
問題集を反復しておけば、才能の無い学生さんでも必ず解けるようになる1問です。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:頑張って完答したい1問
大問2

講師としての解説
「ベクトル」からの出題です
計算量・難易度に関して、やや簡単です。ベクトルの簡単な計算が続きます。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。知識の必要性に関して、やや少なめです。内積が使えれば十分です。
問1に関して、内分点PとQをベクトル表示する問題です。OPベクトルを2種類の方法で表し、イコールでつなぎ、係数比較すれば正解できます。問2に関して、ORベクトルを答えます。線分AMとQRが直交している事から「内積=0」の式が立ちます。内積の式を解くと、辺OAに対する線分ORの「長さの比」が求まるので、OAベクトルにかければ正解となります。問3に関して、問2の条件下で「ORがOAの中点」だった場合を答えます。「問2で求めた長さの比=1/2」の式を解くと正解となります。
受験生としての解説
2006年の九大数学5問で、1番簡単な問題です。
全ての受験生さんが完答しておきたい1問です。2006年の九大数学は、最後の小問まで簡単な大問が本問1つなので、なんとか完答を拾っておきたいところです。
もし解けなかった場合は、次に簡単な大問1・大問4から完答を目指してください。
- 計算:★★(やや簡単)
- 閃き:★(ほぼ不要)
- 知識:★★(やや少なめ)
- 総合:★(簡単)
- 短評:完答したい1問
大問3

講師としての解説
「数列」と「整数」からの出題です。
計算量・難易度に関して、やや難しいです。閃きの必要性に関して、普通程度です。小問1も小問2も数学的帰納法を使えば解けます。知識の必要性に関して、やや強めに必要です。小問2で互いに素な関係を示す際に、互いの因数を「p1p2p3・・・ps」「q1q2q3・・・qt」と置いて計算する定石が必要となります。
問1に関して、証明問題です。anは3で割り切れて、bnは3で割り切れない事を示します。「a1=b1=1」が与えられているので、数学的帰納法に持ち込めば正解できます。bkが3で割り切れない事を表す時「3m+1、3m+2」ではなく「3m±1」と置くと計算が楽になります。問2に関して、証明問題です。anとnbが互いに素である事を示します。問1の流れがあるので、数学的帰納法を使う事は解りやすいです。ポイントは「n=kで成り立つと仮定した時、n=k+1でも成り立つ事を示す」上で背理法を使うことです。普通の数学的帰納法では「n=kで成立」を仮定すると「n=k+1でも成立」が比較的容易に求まりますが、本問は一苦労あります。そこで「n=k+1では成立しない」と仮定して否定する「背理法」を使って数学的帰納法を完成させると正解できます。
受験生としての解説
2006年の九大数学5問で、2番めに難しい問題です。
小問1は、数学的帰納法を使って解く「普通レベル」の問題なので、簡単ではないですが落とすと痛い失点になります。小問2は、因数を「ppp・・・p」「qqq・・・q」と置いて互いに素である事を証明する定石は「医学科限定」というレベルではないのですが、ここまで身に着けなくても九大の非医歯薬系なら合格できます。よって、不正解でも構いません。
2006年の九大数学は、大問2が簡単で、大問1・大問4が比較的簡単なので、この3問を主軸に大問3・大問5から部分点を添えて「2完答+3部分点」を目指してください。
- 計算:★★★★(やや難しい)
- 閃き:★★★(普通)
- 知識:★★★★(やや多い)
- 総合:★★★★(やや難しい)
- 短評:小問1まで正解したい
大問4

講師としての解説
「積分」からの出題です。
計算量・難易度に関して、やや難しいです。2重に絶対値が付いた三角関数のグラフを作図します。その後、xの範囲で場合分けして積分計算をします。閃きの必要性に関して、やや少なめに必要です。作図が複雑ですが、言われた事をするだけの問題です。知識の必要性に関して、普通程度です。絶対値が付いた関数を作図する知識(x軸で反転する)が必要です。
問1に関して、計算問題です。f(x)=0を満たすxを答えます。右辺が「=0」なので、外側の絶対値は無条件にはずせます。-1/2を右辺に移行して内側の絶対値も外すと「=±1/2」となり「sinx=0,1」で平凡な計算へ持ち込んで正解となります。問2に関して、作図です。2重に絶対値が付いた与式を作図します。
- y=sinxのグラフを描く
- y=sinx-1/2(平行移動)
- y=|sinx-1/2|(x軸反転)
- y=|sinx-1/2|-1/2(平行移動)
- y=||sinx-1/2|-1/2|(x軸反転)
という具合に「y=sinx」の式から簡単な順に作図を繰り返せば正解できます。問3に関して、計算問題です。F(a)を計算します。一見、かなり怖そうな計算ですが、問題文の「0≦a≦π/2」に気づけば簡単だと解ります。積分区間は最大でもπ/2までなので、場合分けは2つで済みます。
受験生としての解説
2006年の九大数学5問で、3番めの難易度です。
小問1は、一見難しそうですが簡単なので、全ての受験生さんが正解したい問題です。小問2は、ゆっくり時間をかけて確実に正解したいところです。なぜなら、小問3が最終問題としては簡単であり、実質的に小問2・3でワンセットの大きな配点(約40点)になっているからです。頭を使わなくても、肉体労働でこれだけの点数がもらえるので、才能の無い学生さんほど大事にしたいところです。小問3は、普通の積分計算なので、全ての受験生さんが正解したい問題です。
- 計算:★★★★(やや難しい)
- 閃き:★★(やや少ない)
- 知識:★★★(普通)
- 総合:★★(やや簡単)
- 短評:肉体労働で完答できる
大問5
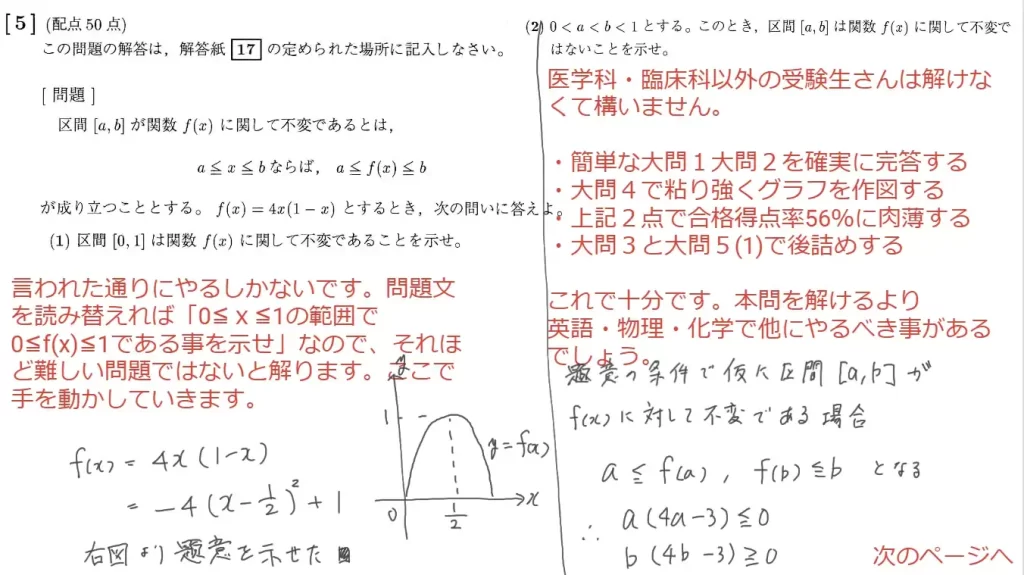
講師としての解説
「二次関数」からの出題です。
計算量・難易度に関して、やや難しいです。問題文で定義された「不変である」条件を受け入れつつ、それに合わせた不等式を自作し、証明を進めます。閃きの必要性に関して、強く必要です。問題文で示された定義を理解し、それを試験現場で応用しなが解答する問題です。知識の必要性に関して、普通程度です。問題で使う定義は問題文で説明してくれているので、普通程度の式変形・作図ができれば正解可能です。
問1に関して、証明問題です。問題文で定義された「不変である」ことを区間[0,1]で証明します。「微分→増減表」から最大・最小値を調べてもよいですが、本問は二次関数なので「平方完成」で正解できます。問2に関して、証明問題です。0<a<b<1なるabにおいて、区間[a,b]が不変でない事を示します。「不変でない事を示せ」なので「不変である」と仮定して矛盾を突く「背理法」を使います。もし不変である場合、問題文の式より「a≦3/4≦b」という関係が成り立ちますが、計算を進め、その領域を作図すると、グラフ上では「不変である」領域が無くなってしまい矛盾します。よって背理法より正解となります。
受験生としての解説
2006年の九大数学5問で、1番難しい問題です。
小問1は、f(x)の増減を調べるだけなので、全ての受験生さんが正解したい問題です。小問2は2006年の九大数学で1番難しいので、医学科・臨床科以外の受験生さんは不正解で構いません。ただ、問題文の言う通りにするだけで「a≦3/4≦b」までは行き着けるので、書いておいた方が良いです。
- 計算:★★★★(やや難しい)
- 閃き:★★★★★(強く必要)
- 知識:★★★(普通)
- 総合:★★★★★(難しい)
- 短評:医学科の合否を分ける問題
九州大学の数学2005年・平成17年度
大問1

講師としての解説
「積分」からの出題です。
計算量・難易度に関して、やや簡単です。回転体の体積を求める問題で、sin2乗の積分があるぐらいです。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。知識の必要性に関して、やや少ないです。積分による回転体の体積計算ができれば十分です。
問1に関して、計算問題です。与えられた2本の式からaの値を導きます。与えられた式は2本ですが未知数がx・y・aの3つなので、自分で式を1本加えれば(連立方程式にすれば)正解できます。加える1本は、直線lが曲線Cの接線である事を立式すればよいです。問2に関して、体積計算です。直線lと曲線Cに囲まれた部分を、x軸中心に回転させた体積を求めます。直線lを回転させた部分から、曲線Cを回転させた部分をくり抜けば正解です。前者は三角錐なので、積分せずとも体積を出せます。
受験生としての解説
2005年の九大数学5問で、1番簡単な問題です。
小問1・小問2ともに
- 難易度が低い
- 九大で頻出の「積分による体積問題」
- 問題集のコピーの様な問題
なので、全ての受験生さんが完答したい大問です。
九大数学は大問5つから「2完答+3部分点」で、非医歯薬系の合格得点率56%を作れます。本問を完答して「残り1完答+3部分点」の状態を作れば、合格点超えは安定します。
- 計算:★★(やや簡単)
- 閃き:★(ほぼ不要)
- 知識:★★(やや少ない)
- 総合:★(簡単)
- 短評:完答したい1問
大問2
「行列」からの出題です。
現在は指導要領の範囲外なので、解説は割愛します。
大問3

講師としての解説
「複素数平面」からの出題です。
計算量・難易度に関して、やや簡単です。軌跡の式に持ち込む部分がややテクニカルですが、数式はシンプルです。閃きの必要性に関して、ほぼ不要です。問題集のコピーの様な問題です。知識の必要性に関して、普通程度です。複素数の式をxy平面の軌跡へ持ち込むために「実部=x、虚部=y」と置き換える定石が必要です。
問1に関して、計算問題です。与式の「異なる2つの虚数解」を求めます。虚数解を持つ条件は「判別式<0」で虚数解は「解の公式」を使えば求まります。ルートの中身に「-1」をかけて「i」を外に出せば正解です。問2に関して、作図問題です。複素数平面上で点zが表す図形を作図します。複素数zの「実部をx、虚部をy」と置き、2式からtを消去するとx・yの式が残り、これを作図すれば正解です。
受験生としての解説
2005年の九大数学5問で、2番めに簡単な問題です。
小問1・小問2ともに「問題集のコピーの様な問題」なので、全ての受験生さんが完答しておきたい大問です。
九州大学は難しい大学ですが、合格するだけなら(2完答+3部分点だけなら)大問1・大問3の完答で可能です。
- 計算:★★(やや簡単)
- 閃き:★(ほぼ不要)
- 知識:★★★(普通)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問4

講師としての解説
「対数」と「三角関数」からの出題です。
計算量・難易度に関して、難しいです。高校指導要領の範囲外である「ガウス記号」の計算が続きます。閃きの必要性に関して、やや強めに必要です。問題文で説明された定義を受けれ、それを試験現場で応用するタイプです。知識の必要性に関して、強く必要です。指導要領の範囲外である「ガウス記号」の定石を身に着けておく必要があります。
問1に関して、計算問題です。与式を満たす「θの範囲」を求めます。三角関数にガウス記号、対数まで付いた複雑な式なので、簡単な部分から順に攻めていきましょう。まず、与式の中で最もシンプルな「cosθ」だけを見ます。条件より「-1<cosθ<1」と解ります。次は「+5/2」しましょう。「3/2<5/2+cosθ<7/2」となります。次はいよいよ「ガウス記号」を付けます。ガウス記号は定義で憶えると難しいので、慣れるまでは「小数点切り捨て」と憶えておけば良いです。よって、ガウス記号を付けると [5/2+cosθ]=1,2,3 となります。そして「log」を付ければ、与式と同じ形になります。log2[5/2+cosθ]=0,1,log3です。よって「与式≦1」より「5/2+cosθ<3」(←つまり2.9999・・・まではOKという事)とハッキリし「π/3<θ<π」が正解と解ります。こうやって簡単な順に組み立てていけば、見た目ほど難しくありません。問2に関して、計算問題です。基本的に問1と同じ方針で解けます。
- 問題文の条件より:[3/2+logsinθ]≧1
- 計算結果より:[3/2+logsinθ]≦1
- 上記2点より:[3/2+logsinθ]=1
と導く部分がやや難しいです。医学科用の超難関問題集で練習しておけば普通と思えます。問3に関して、計算問題です。与式の満たすθの範囲を答えます。問1・問2を応用すると、与式を満たすのは
- 「左辺=0,1」かつ「右辺=1」
- 「左辺=0」かつ「右辺=0」
の2パターンしかない事が判ります。よって各々のθの範囲を求め、最後に合体させれば正解となります。
受験生としての解説
2005年の九大数学5問で、1番難しい問題です。
上記解説の通り、ガウス記号の定石さえ知っておけば小問2までは普通の問題です。だから、学校や予備校は「九大に行きたいなら全部勉強しろ」というわけですが
- ガウス記号の九州大学での出題確率
- 英語・物理・化学への負担
を考えた時、才能に恵まれた「トップ高校の学生さん」以外には効率が良くないです。よって本問は、小問1から不正解でも構いません。
2005年は大問1・大問3が簡単なのでこの2問を完答し、大問2・大問5から多めに部分点を稼げば、非医歯薬系の合格得点率56%に届きます。
- 計算:★★★★★(やや難しい+ガウス記号=難しい)
- 閃き:★★★★(やや強く必要)
- 知識:★★★★★(強く必要、高校の範囲外)
- 総合:★★★★★(難しい)
- 短評:医学科の合否を分ける問題
大問5
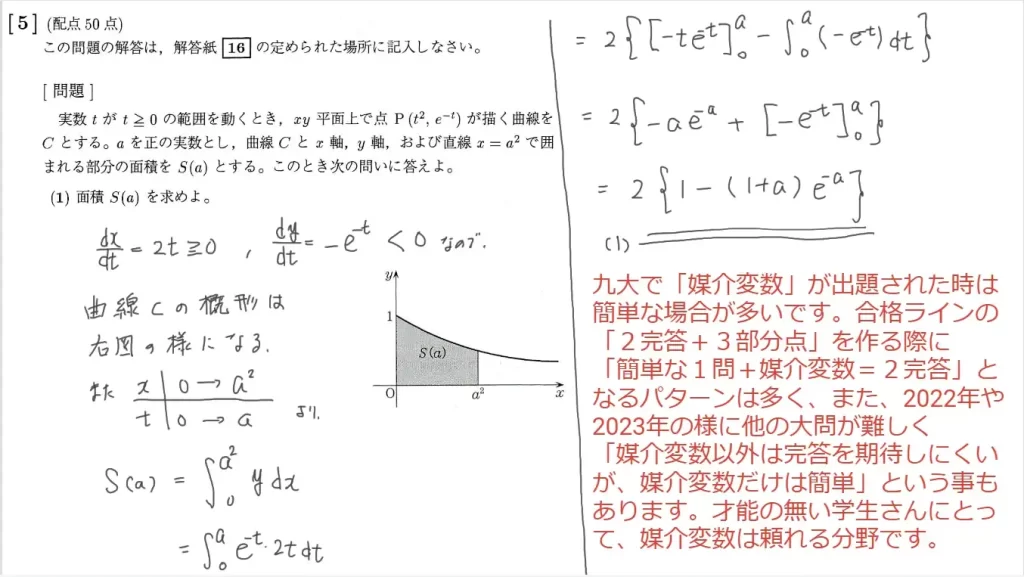
講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、普通程度です。小問2までの微分・増減表・作図は容易です。小問3で不等式を自分で設定し、中間値の定理に持ち込む部分がやや難しいです。閃きの必要性に関して、普通程度です。小問3まで含めて「問題集のコピーの様な問題」ですが、コピーとはいえ自分で不等式を設定して値を評価する事は思考を要します。知識の必要性に関して、普通程度です。微分、増減表、不等式、中間値の定理の知識が必要です。
問1に関して、計算問題です。x・yを媒介変数tで微分すると「xは単調増加、yは単調減少」と判ります。また、yの極限値が0でx・yが(0,1)を満たすので曲線Cの概形が解り、積分すれば面積Sが求まります。問2に関して、作図問題です。問1で求めたSを「aの関数」とみなし、y=S(a)のグラフを作図します。よって、グラフの凹凸まで知る必要があるため「2回微分」を使い、増減表を書けば正解できます。問3に関して、証明問題です。S(a)=1.35を示せという事なので、S(a)-1.35=0を示す方が楽です。S(a)-1.35が連続である事に加え、a=2では0を下回り、a=3では0を上回るため、2<a<3の間で0丁度になる値が存在して証明終了となります(中間値の定理)
受験生としての解説
2005年の九大数学5問で、3番めの難易度です。
小問1に関して、媒介変数を微分してグラフを描き積分計算するだけなので、全ての受験生さんが正解したい問題です。小問2に関して、2回微分して増減表を描きグラフを作図するだけなので、全ての受験生さんが正解したい問題です。小問3に関して、合否を分ける1問です。不合格になる学生さんが丁度解けない1問という感じです。
- 不等式を自分で設定する
- 中間値の定理を使う
と考えてしまうと難しくなります。そうではなく
- グラフの左側が1.35より下に来て
- 右側が1.35より上に来る事を示したい
- そうすればピッタリ1.35になる点が必ずある
と、最初から目的を持っておけば中間値の定理を使う事が「当たり前」となり、不等式を自分で設定する事も「当たり前」となるため、不等式の設定が簡単と思えるようになります。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:完答したい1問
九州大学の数学2004年・平成16年度
大問1

講師としての解説
「積分」からの出題です。
計算量・難易度に関して、やや難しいです。積分を絡めた不等式を扱い、シグマ記号からはさみうちの原理、小問1を応用した式変形とバラエティに富んだ計算内容です。閃きの必要性に関して、普通程度です。難関大の計算としては妥当なレベルです。知識の必要性に関して、普通程度です。上記の幅広い知識を使った一連の流れを知っておけば正解できます。やや難しいですが定番の流れでもあります。
問1に関して、計算問題です。「InとIn-1」の関係を求め、I0・I3の値を答えます。I0に関してはn=0を代入すればすぐ正解できます。Inに含まれる積分を「部分積分」で計算するとIn-1が出てくるので、関係式を作れて正解となります。出てきた関係式にn=1・2・3と順に代入していくとI3が求まり完答となります。問2に関して、証明問題です。与えられた積分の不等式を証明します。与式の形から「数学的帰納法」を使えば速く安全に解けそうだと想像できます。n=1で成り立つ事は明らか、n=kで成り立つと仮定してn=k+1でも成り立つ事を示す部分も、不等式の両辺を3倍するだけなので難しくありません。問3に関して、極限を求める問題です。与式の形が小問1の「In-In-1」と同じである事に気付いて置き換えます。与式の形に近づけるためシグマ記号を付けるとInの式が残り、小問2の結果とはさみうちの原理より正解が求まります。難しいですが、問題集のコピーの様な問題なので、訓練すれば誰でもできるようになります。
受験生としての解説
2004年の九大数学は、5問とも同程度の難易度です。2004年から選択問題が廃止され「全問必答」へ変わった影響と思われます。
小問1は、全ての受験生さんが正解したい問題です。Inをそのまま計算すればIn-1が出てきそうな事は想像できるようになっておきたいところです。練習すれば才能が無くてもできるようになります。小問2は、全ての受験生さんが正解したい問題です。与式の形から数学的帰納法を使うだろうと予測が立ちます。小問3は、合否を分ける1問です。小問1・小問2を応用し、式変形から「はさみうちの原理」に持ち込む事は難関大学の定番ですが、簡単ではありません。同時に、簡単ではないが定番です。訓練すれば誰でもできるようになります。練習量が問われる1問となっています。
解けない場合は小問5「場合の数・確率」小問3「媒介変数」に時間を回してください。この2問は時間をかければ得点しやすく、難易度も程々です。
- 計算:★★★★(やや難しい)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:小問2まで正解したい
大問2
「行列」からの出題です。
現在は指導要領の範囲外なので、解説は割愛します。
大問3

講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、普通程度です。速度ベクトルの計算、対象点の計算、微分して増減表、置換積分など普通の事を幅広く問われています。閃きの必要性に関して、やや少なめです。x軸・y軸に対象な図形である事をふまえて作図する際に、やや思考を要します。知識の必要性に関して、やや少なめです。対象点の表示、増減表からの作図、置換積分などです。
問1に関して、計算問題です。点Pが原点を通る時の速度ベクトルを求めます。点P(0,0)の式における時間tを求め、それをx・yを微分した式に代入すれば正解できます。問2に関して、証明問題です。点Pの軌跡Cが「x軸にもy軸にも対象」な図形である事を示します。点Pのy座標に-1をかけた点Qとx座標に-1をかけた点Rを用意し、点Q・点Rが点Pの式を満たしている事を示せば正解できます。問3に関して、作図問題です。点Pの軌跡Cを作図します。問2で「x軸・y軸に対象」である事を示したので、第1象限だけ計算で求め、残りは反転コピーで作図できます。作図に際してはdy/dxから増減表を書くいつもの流れです。問4に関して、計算問題です。作図した図形が囲む面積を答えます。問2で「x軸・y軸に対象」である事を示したので、第1象限だけ面積計算し、それを4倍すれば楽ができます。積分に際しては媒介変数の積分に持ち込んでください。
受験生としての解説
2004年の九大数学は、5問とも同程度の難易度です。2004年から選択問題が廃止され「全問必答」へ変わった影響と思われます。
小問1に関して、s=0とy=0を代入し与式を微分するだけなので、全ての学生さんが正解したい問題です。小問2に関して、x軸・y軸の対象点は大半の問題集に類問が載っており、同時に難しくないので、全ての学生さんが正解したい問題です。小問3に関して、増減表からの作図も大半の問題集に載っており、同時に難しくないので、全ての学生さんが正解したい問題です。小問4に関して、媒介変数による面積計算も大半の問題集に載っており、同時に難しくないです。全ての学生さんが正解したい問題です。
普通の事が普通に問われている基本的な問題なので、全ての学生さんが完答しておきたい1問です。九大非医歯薬系の合格得点率56%は、出題5問から「2完答+3部分点」で作れます。本問を完答し、残り4問から「1完答+3部分点」の状態を作っておけば、才能の無い学生さんでも安定して九大の合格点を取れます。
- 計算:★★★(普通)
- 閃き:★★(やや少なめ)
- 知識:★★(やや少なめ)
- 総合:★★(やや簡単)
- 短評:普通の事が普通に問われている1問
大問4

講師としての解説
「ベクトル」からの出題です。
計算量・難易度に関して、普通程度です。ベクトルに関するやや煩雑な計算が続き、小問3では場合分けが発生します。閃きの必要性に関して、普通程度です。小問2までは閃く要素はありませんが、小問3で場合分けする際に思考を要します。知識の必要性に関して、やや少ないです。ベクトルの基本知識だけで正解できます。
問1に関して、計算問題です。OAベクトル・OCベクトルに直交する単位ベクトルを求め、OBベクトルとの内積を答えます。求める単位ベクトルをe=(x,y,z)で仮定すると
- |e|=1
- eベクトル ⊥ OAベクトル
- eベクトル ⊥ OCベクトル
で式が3本立ち、「未知数3つ、式3本」で連立方程式を解けば正解できます。本問が正解できる事は大事ですが、それ以外に「何をしているのか」が見えるようになってください。
- 「OAベクトル・OCベクトルと直交」というのは、平面OACに垂直である事、つまり四面体の底面をOACに設定していること
- 「OBベクトルとの内積」は点Bから面OACに下ろした垂線を「高さ」に設定していること
これが見えるようになれば、小問2以降で行き詰まる事を減らせます。問2に関して、計算問題です。四面体OABCの体積を答えます。小問1でそろえた材料を使い
- 三角形OACの面積
- 四面体の高さ
を計算して「底面積×高さ×1/3」で正解できます。問3に関して、体積の最大値を求める問題です。問2で求めた体積の式を基に、体積が最大となる点A点Bの位置を割り出します。体積を表す式の形が決まっているので
- bcの項が0の時
- d(a-b)の項が0の時
- どちらの項も0でない時
の3パターンについて最大値を求め、3つ中から更に最大となるものが本当の最大値となります。
受験生としての解説
2004年の九大数学は、5問とも同程度の難易度です。2004年から選択問題が廃止され「全問必答」へ変わった影響と思われます。
小問1に関して、言われた通りの計算をするだけなので、全ての受験生さんが正解したい問題です。ただ正解するだけでなく、小問2の材料になっている事を見抜いておきたい問題です。小問2に関して、合否を分ける1問です。四面体の体積計算をしているだけなので、全く難しくないです。しかし、ベクトルの基礎が不足しており、小問1で手一杯だった学生さんはここで脱落し、痛い失点となります。これは避けたいところです。小問3に関して、医学科限定と言うほど難しくはありませんが、非医歯薬系なら不正解でも合格できます。正解できたら大きな追加点という感じです。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★(やや少なめ)
- 総合:★★★(普通)
- 短評:小問2まで正解したい
大問5

講師としての解説
「場合の数・確率」からの出題です。
計算量・難易度に関して、普通程度です。小問3まで計算らしい計算はありませんが、小問4の期待値計算がやや難しいです。閃きの必要性に関して、普通程度です。小問3の「m回」で一工夫必要になります。知識の必要性に関して、やや少ないです。確率計算とシグマ記号が使えれば十分です。
問1に関して、確率計算です。電球の光り方が「1回だけ」変わるという事は、n個の電球から「左端を除く1個」を選ぶ事に等しいため「n-1通り」となります。問2に関して、確率計算です。色の変化が「少なくとも2回起きる」という文言から「0回・1回だけ起きる確率」を調べれば正解できると解ります(余事象)問3に関して、確率計算です。電球の光り方が「m回変化」するという事は、n個の電球に存在する「n-1個のスキマ」から「m個」を選ぶ事に等しいです。これに気づけば正解できます。問4に関して、計算問題です。問3までの結果を基に、電球の光り方が変わる期待値を答えます。問3で「m回」という一般化された形で確率を出してきたので、それをシグマ記号で集めてあげれば正解できます。計算がやや難しいですが、シグマ記号の計算ドリルを練習しておくと不安を解消できます。
受験生としての解説
2004年の九大数学は、5問とも同程度の難易度です。2004年から選択問題が廃止され「全問必答」へ変わった影響と思われます。
小問1・小問2は、共通テストより簡単なので、全ての受験生さんが正解したい問題です。小問3に関して、合否を分ける1問です。「n-1個のスキマから」と発想を変える事は簡単ではありませんが、九大受験では不合格者でも正解してくるレベルなので、落とすと痛い失点となります。小問4に関して、合否を分ける1問です。小問3と異なり不合格者には難しいレベルですが、「医学科限定」というほど難しくもありません。落とすと痛い失点となり、正解できれば合格への大きな1歩となります。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★(やや少なめ)
- 総合:★★★(普通)
- 短評:完答したい1問
九州大学の数学2003年・平成15年度
大問1

講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、やや難しいです。媒介変数の微分積分から回転体の体積を出す定番の流れですが、計算がやや複雑です。閃きの必要性に関して、普通程度です。小問1・小問3は「問題集のコピーの様な問題」なので閃きはほぼ不要ですが、小問2の証明でやや思考を要します。知識の必要性に関して、普通程度です。媒介変数の積分による体積計算の流れ、部分積分を変形させた証明問題の定石を知っておく必要があります。
問1に関して、作図問題です。媒介変数で表示される曲線Cを作図します。x・yをtで微分し、増減表を書けば曲線Cの形が見えます。問2に関して、証明問題です。問3で行う積分計算の数値が複雑なので、それを簡略化する数式を証明します。部分積部でかけ算となる2要素を「u、v」と置き、uとvに問題文で指定された数式を代入すると正解できます。問3に関して、計算問題です。問1で作図した曲線Cを、x軸周りに1回転してできる立体の体積を答えます。x方向の式では数値が複雑なため、問1で用いた媒介変数tの積分に置き換えます。それでも計算過程が複雑なので、今度は問2で証明した数式に代入し、簡略化した計算を終えると正解となります。
受験生としての解説
小問1に関して、媒介変数の微分~積分による体積計算は定番の流れなので、全ての受験生さんが正解しておきたい問題です。小問2に関して、合否を分ける1問です。左辺のインテグラルの中に微分されたr(ダッシュがついたr)があるので、そこから「部分積分」と気づいた人が正解できます。配点的にもレベル的にも「九大非医歯薬系の合格ライン」という感じです。小問3に関して、小問2を正解できた人には難しくない問題です。よって、小問2の結果により
- 小問1だけ正解できた学生さん
- 完答(小問3まで正解)できた学生さん
に分かれやすい、30点以上の差がつきやすい出題でした。小問2は見た目がかなり難しそうですが、やっている事は「u・v」の形になった部分積分の変形でしかありません。問題集で訓練すれば、才能の無い学生さんでも必ずできるようになります。
- 計算:★★★★(やや難しい)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:小問2が合否を分ける1問
大問2

講師としての解説
「図形と領域」からの出題です。
計算量・難易度に関して、普通程度です。絶対値が2つ含まれた不等式を丁寧に解読し、その後は「絶対値の中に絶対値が含まれた式」の解読へつなげます。閃きの必要性に関して、やや強めに必要です。小問2で絶対値の中の絶対値を開き図形を見出す事、小問3で「素因数の一致」を正解の理由にする事など、思考力が必要となります。知識の必要性に関して、やや多く必要です。絶対値の外し方、整数の運用、有理数の定石、作図、それらを柔軟に使いこなす必要があります。
問1に関して、作図問題です。xの項・yの項について、絶対値の中身を正負で場合分けし、絶対値をはずしてください。4本の式が出てくるので、それら4直線に囲まれた部分が正解となります。問2に関して、作図問題です。問1で用いた式の絶対値の中にもう1つ絶対値が含まれています。新しく加わった絶対値によって
- xの符号が反転する事は「y軸対称」を
- yの符号が反転する事は「x軸対称」を
意味します。よって、問1で求めた図形が「x軸反転・y軸反転・xy両軸反転」で3つ増えたものが正解となります。問3に関して、計算問題です。問2で求めた図形において、logx|y|が有理数となるようなx・yの値を「理由を示して」答えます。問2の図形より「xが正の整数」という条件が付けば「x=3・4・5」の3パターンしかありません。よって、この3パターンに関して「yが整数になるもの」をリストアップし、そこから更に「logx|y|が有理数になるもの」を導き出せば正解できます。有理数なので「=q/p」と置いて式変形します。左辺がq乗、右辺がp乗に分かれるとはいえ「=」でつながれた同じ数なので、最低でも「素因数」が共通でなければなりません。この組み合わせを満たすx・yの組み合わせが正解となります。
受験生としての解説
小問1に関して、絶対値をはずして作図するだけなので、全ての受験生さんが正解したい問題です。小問2に関して、絶対値の中の絶対値をはずす事により「小問1の図形が上下鏡写しで4倍に増える」という事実がやや難しいので、合否を分ける1問となります。簡単に正解できる問題ではありませんが、本問を不正解になって「小問1だけ正解=約10/50点」だと、他の問題で取り返す必要があります。小問3に関して、解ければ他者に差をつけられる1問です。やや難しい小問2をクリアせねば本問に参加できないわけですが、それでも「医学科限定」というほど難しくはありません。本問を正解できれば小問2と合わせて、小問1で脱落したライバルに大きく差を(約35点)つける事ができます。
- 計算:★★★(普通)
- 閃き:★★★★(やや強く必要)
- 知識:★★★★(やや多い)
- 総合:★★★★(やや難しい)
- 短評:頑張って小問2まで正解したい
大問3

講師としての解説
「積分」からの出題です。
計算量に関して、難しいです。x・y・1/p乗・Dn・Mn・Ln・Snと様々な記号を使います。閃きの必要性に関して、やや強めに必要です。試験現場で提示されたルールを理解し、その場で応用するタイプの問題です。知識の必要性に関して、やや強く必要です。格子点に関する定石を知っておく必要があります。
問1に関して、証明問題です。与式のグラフが交わる単位正方形の数がn個である事を証明します。与式のxに関して、自然nについて「n→n+1」と1ずつに区切って考えると、その区間において交われる単位正方形の個数が「1個しかない」事が判ります。よってxの範囲を「0≦x≦n^1/p」と拡張すると、交われる単位正方形の個数はn個と証明できます。問2に関して、証明問題です。与えられた不等式を証明し、更に面積Snを答えます。与式の左辺に関して、領域Dnに含まれる単位正方形の数がMnであり、Dnの面積がSnなので「Sn≦Mn」が成り立ちます。また、問1の結果より(Mn+n)個の正方形の中に領域Dnが含まれているため「Sn≦Mn+n」である事も解ります。最後に、y=x^1/pの傾きが常に有限であることから不等式の「=」を消せるため、証明終了となります。また、面積Snはy^1/pを0≦y≦nの範囲で積分すると求まります。問3に関して、極限値を求める問題です。領域Dnの性質より、Dnに含まれる正方形の個数はMnと解ります。問1の結果より「Sn-n<Mn<Sn」である事が解ります。真ん中のMnを問題文で指定された形に式変形し、両脇の極限を取るといずれもp/p+1となるため「はさみうちの原理」より正解できます。
受験生としての解説
小問1~小問3に関して、非医歯薬系の受験生さんには厳しいレベルなので、不正解でも構いません。
大問1「媒介変数」など、簡単な問題から確実に点数を拾ってください。
- 計算:★★★★★(難しい)
- 閃き:★★★★(やや強く必要)
- 知識:★★★★(やや難しい)
- 総合:★★★★★(難しい)
- 短評:医学科の合否を分ける問題
大問4A

講師としての解説
「ベクトル」からの出題です。
計算量・難易度に関して、普通程度です。ベクトルの計算が続きます。閃きの必要背に関して、やや少ないです。問題集のコピーの様な問題です。知識の必要性に関して、やや少ないです。ベクトルの基本知識があれば正解できます。
問1に関して、計算問題です。∠OGA、∠OGB、∠OGCが全て90°だった場合に「a、b、cの間に成り立つ関係」を答えます。ポイントは「90°」という角度で「内積=0」の式を立てれば正解できます。問2に関して、線分OQの最小値を求める問題です。
- 線分BCを1:2に内分する点D
- 点PはAD上のA以外を動く点
- 点Qは三角形APQの重心が点Gになるように動く
など、条件が付与されています。ポイントは「ゴールから考える事」です。複雑な条件下ですが、最後は「|OQ|=」の形になると解っています。よって、ゴールから逆にたどり
- OQベクトルが分かればよい
- OQベクトルはOGベクトルで表せる
- そのためにはOAベクトル・OPベクトルが必要で、OAベクトルは既に明らか
- OPベクトルはOAベクトル・ODベクトルで表せる
- ODベクトルはBCの内分点なのですぐ表せる
- スタート地点
となり、上記を下から順に立式すれば正解できます。
受験生としての解説
2003年の九大数学9問で、1番簡単な問題です。
選択問題4A~4Cの中で、1番簡単な問題です。
小問1に関して、「すべて90°」より「内積=0」を使う事が明らかなので、全ての受験生さんが正解したい問題です。小問2に関して、共通テストより少し複雑な程度なので、不合格者でも正解してきます。よって、落とすと痛い1問となります。
- 計算:★★★(普通)
- 閃き:★★(やや少ない)
- 知識:★★(やや少ない)
- 総合:★★(やや簡単)
- 短評:完答したい1問
大問4B

講師としての解説
「複素数平面」からの出題です。
計算量・難易度に関して、普通程度です。小問1はシンプルですが、小問2で軌跡の式に三角関数が入って複雑化します。閃きの必要性に関して、普通程度です。小問2において複素数の特性である「回転の容易さ」を活用し、交点の数を「二次方程式の解の個数」に帰着させます。知識の必要性に関して、普通程度です。複素数、三角関数、軌跡、作図の知識を使います。
問1に関して、作図問題です。与式zが直線l上を動く時の「z2乗の軌跡」を作図します。軌跡を求める問題なので、計算の終了形は「xとyの式」となる事が解ります。よって「z^2=x+yi」と置き、問題文で与えられた「zの式」を使って「t」を消去してあげれば正解できます。問2に関して、交点の個数を数える問題です。問1で描いた作図と、直線lを原点中心で回転させた直線mの交点の数を答えます。直線lの軌跡は問題文で「z」と表されており、この直線を原点中心にθ回転させた直線mは z(cosθ+isinθ) と表す事ができます。この式の「実部をx、虚部をy」と置き、双方からtを消去すると直線mの式が現れます。そして、問1で求めた「軌跡の式」と連立させ、双方からxを消去して「yの二次方程式」に持ち込み、判別式から解の個数を数えれば、それが求める「交点の数」となり正解できます。
受験生としての解説
選択問題4A~4Cの中で、2番めに簡単な問題です。
小問1に関して、軌跡の基本問題なので、全ての受験生さんが正解したい問題です。小問2に関して、「回転→軌跡→判別式→場合分け」と複数の基礎を複合的に問われているので、合否を分ける1問となっています。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:完答したい1問
大問4C
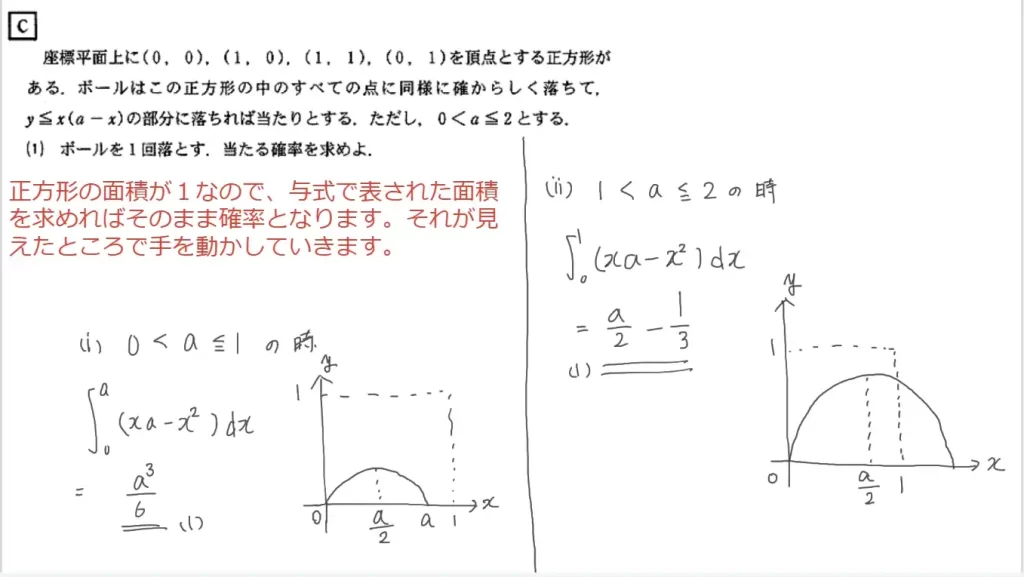
講師としての解説
「場合の数・確率」と「積分」からの出題です。
計算量・難易度に関して、やや簡単です。シグマ記号を使わずに正解できるため、計算を難しくせずに済みます。閃きの必要性に関して、普通程度です。問2までは問題集のコピーの様な問題ですが、問3でやや思考を要します。知識の必要性に関して、やや少ないです。確率計算と定積分の知識があれば十分です。
問1に関して、確率計算です。面積が1の正方形(縦1✕横1)にボールを落としy≦x(a-x)の範囲に落ちる確率を求めます。与式の境界線はxの二次方程式であり、その軸(x=a/2)が
- 正方形の内側(0<a/2≦1)
- 正方形の外側(1<a/2≦2)
で場合分けが発生します。後は定積分の計算で正解です。問2に関して、確率計算です。ボールを2回落とした時に1回だけ当たる確率を答えます。1回ごとの確率は、問1の計算式にaの値を代入すれば求まります。後は「1回目だけ当たる確率+2回目だけ当たる確率」で正解です。問3に関して、aの値の範囲を答える問題です。問題文に「少なくとも1回は確率」と書いてあるので「1回も当たらない確率」を求め、100%から引き算してあげれば正解できます。期待値計算は、試行回数が3回しかないので1~3回目の確率を書き出し、それぞれに1・2・3をかけて足し合わせれば正解できます(医学科の受験生さんなら「k回目の期待値」と一般化し、シグマ記号を付けて一気に正解してください)
受験生としての解説
選択問題4A~4Cの3問で、2番めに簡単な問題です。
問1・問2に関して、共通テストと大差ないレベルなので、全ての受験生さんが正解したい問題です。問3に関して、九大理工系の合格レベルより少し簡単です。よって、不合格者さんでも正解してくるので、落とすと痛い1問となります。
大問4はA~Cまでそれほど難しくなく、選択もできます。大問4を完答し、残り4問から「1完答+3部分点」の状態を作れれば、才能で劣る学生さんでも安定して非医歯薬系の合格点(2完答+3部分点=得点率56%)を取れるようになります。
- 計算:★★(やや簡単)
- 閃き:★★★(普通)
- 知識:★★(やや簡単)
- 総合:★★★(普通)
- 短評:完答したい1問
大問5D
「行列」からの出題です。
現在は指導要領の範囲外なので、解説は割愛します。
大問5E

講師としての解説
「微分」からの出題です。
計算量・難易度に関して、普通程度です。tanの加法定理、x・yの方程式を双曲線の式へ導く計算などがあります。閃きの必要性に関して、普通程度です。問2において、点Pの軌跡を傾きm1・m2を使って表し、それを問1の正解に代入する部分でやや閃きが必要です。知識の必要性に関して、普通程度です。2本の接線がx軸となす角をα・βと置き「θ=α-β」から解き進める定石を使います。
問1に関して、tanθを接線の傾きm1・m2を使って表す問題です。放物線の2つの接線PQ・PRがx軸となす角をα・βとおくと、tanα・tanβは接線の傾きm1・m2となります。また、この時「tanθ=tan(α-β)」となるため、加法定理より「tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)=(m1-m2)/(1+m1m2)」で正解となります。
問2に関して、∠QPR=θを満たす点Pの表す図形Gを数式で答えます。図形Gは点Pが0<θ<π/2を満たしながら動いてできるものなので、点Pを数式で表す必要があります。そこで、点Q・点Rのx座標をx1・x2と置いて接線方程式を立てると、これらの傾きがm1・m2に対応するため、x1・x2をm1・m2で表す事ができます。そして、2本の接線の交点が点Pなので、点Pのx座標・y座標をm1・m2で表す事ができます。計算結果は、点P(a,b)=(m1+m2,m1m2)です。よって、今度はm1・m2をa・bで表す事ができ、問1のtanθの式にm1・m2を代入してa・bで表したものが正解となります。
問3に関して、θ=π/4の時のGを作図します。問2で求めたGの式にθ=π/4を代入し、(a,b)を(x,y)に戻して式を整理すれば正解できます。x・yについて平方完成し、定数項の絶対値が1になるように全体を割算してあげると、双曲線の式が出てきます。
受験生としての解説
小問1に関して、接線がx軸となす角をα・βと置き「θ=α-β」から条件を詰めていく事は定石なので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
小問2に関して、軌跡問題の定石通りではありますが、不合格者さんには厳しいレベルであり合格者さんなら正解できるレベルなので、合否を分ける1問となります。
小問3に関して、問2の計算結果にθ=π/4を代入して作図するだけなので、不合格者さんでも正解してくるレベルです。ただし、小問2の正解が必要となるため、合否を分ける1問となります。
小問3が小問2の付け足し(小問2が解けた人へのボーナス点)になっているため
- 小問1だけ正解できた人(約10点)
- 完答できた人(約50点)
と、点差が付きやすい1問となっています。
- 計算:★★★(普通)
- 閃き:★★★(普通)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:小問1の正解だけではやや物足りない
九州大学の数学2002年・平成14年度
大問1
「微分積分」からの出題です。
計算量・難易度に関して、やや難しいです。問2は積分による面積計算なので簡単そうですが、∫√x^2+1dxをまともに計算しに行くと少し厄介です。問1の結果を上手に利用してください。閃きの必要性に関して、やや簡単です。作図をすると台形と三角形が現れますので、これを利用すると計算量を減らせます。知識の必要性に関して、やや簡単です。微分して増減表、積分による面積計算です。
問1に関して、点P(x,y)に対しyをxで表す問題です。
\(x=\dfrac{e^{t}-e^{-t}}{2}\)・・・①
\(y=\dfrac{e^{t}+e^{-t}}{2}\)・・・②
①+②より
\(x+y=e^{t}\)
①-②より
\(y-x=e^{-t}\)
よって
\(\left( x+y\right) \left( y-x\right) =e^{t} e^{-t}=1\)より
\(y^{2}-x^{2}=1\)
今、y>0なので
\(y=\sqrt{x^{2}+1}\)(これが正解です)
問2に関して、面積計算です。線分MPと曲線Cで囲まれたS(t)および、線分OM・線分OP・曲線Cで囲まれたA(t)を答えます。各線の上下関係については計算で証明してもよいですが、簡単な作図をすれば大丈夫です。
- S(t):線分MPとx軸による台形-∫曲線C=(e^t-e^-t)/4 – t/2(これが正解です)
- A(t):∫曲線C-線分OPとx軸の三角形=t/2(これが正解です)
問3に関して、A(t)-S(t)の最大値を計算します。F(t)=A(t)-S(t)とおきます。微分すると「F'(t)=-e^-t/4(e^2t-4e^t+1)」となり増減表は以下のようになります。
| t | 0 | log(2+√3) | ||
| F'(t) | + | 0 | – | |
| F(t) | ↗ | 極大 | ↘ |
よって「t=log(2+√3)」が正解です。
受験生としての解説
問1に関して、式①と式②が独特の形なので、足し引きすれば何か起こる事は見えやすいです。その後の展開も簡単なので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
問2に関して、積分で面積計算するだけなのですが、計算がやや難しいです。合格者さんは正解しますが不合格者さんには厳しいので、合否を分ける1問です。
問3に関して、微分して増減表を書いて極大値を求めるだけなので、不合格者さんでも正解してきます。しかし、本問に参加するためには問2の正解が必要なため、問2とセットで、合否を分ける1問です。
- 計算:★★★(普通)
- 閃き:★★(やや簡単)
- 知識:★★★(普通)
- 総合:★★★(普通)
- 短評:完答したい1問
大問3
講師としての解説
「微分積分」からの出題です。
計算量・難易度に関して、やや難しいです。不等式の証明3連発という事で、気の利いた式変形を要求されています。閃きの必要性に関して、やや難しいです。前問を活用できる形を自分で見つけて式変形する必要があります。知識の必要性に関して、普通程度です。微分積分と増減表で正解できます。
問1に関して、証明問題です。「左辺≧0」を示すという事で、ここは素直に「F(x)=左辺」と起き、微分から増減表に持ち込みます。この際、yは固定して考えます。
- F(x)=(与式の左辺)=xlogx-x(logy+1)+yとおくと
- F(x)’=logx-logyより増減表は以下の通りとなります
| x | 0 | y | ||
| F(x)’ | – | 0 | + | |
| F(x) | ↘ | 0 | ↗ |
よって、F(x)≧0より題意を示せました。なお、等号成立は「x=y」となります。
問2に関して、証明問題です。問1を利用する問題である事は雰囲気で解りますが、問1から大きく姿が変わっているため、どう問1を利用してよいか見えません。そこで、とりあえず、問1の式を「x=f(x)、y=g(x)」と置き換え、何か見えてくる事を期待します。
- f(x)>0、g(x)>0と問1の結果より
- f(x)logf(x)-f(x)logg(x)-f(x)+g(x)≧0
- ∴ ∫{f(x)logf(x)-f(x)logg(x)-f(x)+g(x)}dx≧0(積分区間はa~b)
- ∴∫{f(x)logf(x)-f(x)logg(x)}dx≧0(問題文の条件より、∫f(x)dx=∫g(x)dxなので)
- ∴ ∫f(x)logf(x)dx ≧ ∫f(x)logg(x)dx(証明完了)
問3に関して、証明問題です。問2と同様、前問題から姿が大きく変わっています。しかし、問題文の「正の実数M」という文言より、ある式変形を見出すことができます。
- Mは正の実数なので、与式より
- ∫f(x)dx=(b-a)M=∫Mdx(積分区間はa~b)
- ここでM=g(x)とおくと、問2の結果より
- ∫f(x)logf(x)dx ≧ ∫f(x)logMdx = logM∫f(x)dx
- ここで両辺をb-a(>0)で割ると
- 1/b-a∫f(x)logf(x)dx ≧ logM・1/b-a∫f(x)dx=MlogM
- よって題意を証明できた(証明完了)
受験生としての解説
問1に関して、「F(x)=左辺」とおいて微分から増減表で正解が求まるので、不合格者さんでも正解してきます。よって、全ての受験生さんが正解したい問題です。
問2に関して、問1の条件を利用する問題としては、見えやすいです。よって、合格者さんは正解してくるので、合否を分ける1問です。
問3に関して、「Mが実数だから」という理由で「(b-a)M=∫Mdx」と、普段の積分計算と逆操作する事は合格者さんでも難しいです。よって、正解できれば他者に差をつける1問となります。
- 計算:★★★★(やや難しい)
- 閃き:★★★★(やや難しい)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:問1は落とせない、できれば問2まで解きたい
大問4A
講師としての解説
「空間ベクトル」からの出題です。
計算量・難易度に関して、難しいです。煩雑な計算が続きますが、特に問3で正解が「場合分け」すると気付く部分が難しいです。閃きの必要性に関して、やや難しいです。問2で傾いた立体に対応する部分、問3で△ACPの式を見て「最小値になる条件」を見抜くことなどです。知識の必要性に関して、普通程度です。問1で「面積公式の証明」があります。
問1に関して、公式の証明です。
- ⊿ABC=1/2|→AB||→AC|sinθ
- =1/2|→AB||→AC|√(1-cos²θ)
- =1/2|→AB||→AC|√{1-(→AB・AC/|→AB||→AC|)²}
- =1/2√{|→AB|²|→AC|²-(→AB・AC)²}
以上より証明完了です。
問2に関して、面積計算です。△ACPの面積を求める問題なので、問1を応用して「△ACP=1/2√(|→AC|²|→AP|²-(→AC・AP)²)」となります。よって、欲しいのは
- |→AC|
- |→AP|
- →AC・AP
の3つとなります。ここで点Aを基点に考えると
- →AC=(1,1,0)
- →AP=(x+2cosθ,y,2sinθ)
なので
- |→AC|²=2
- |→AP|²=(x+2cosθ)²+y²+4sin²θ
- →AC・AP=x+2cosθ+y
となるため「△ACP=\(\dfrac{1}{2} \sqrt{\left( y-x-2 \cos \theta \right) ^{2}+8 \sin ^{2}\theta }\)」が正解となります。
問3に関して、△ACPの最小値を求める問題です。ポイントを以下に記します。
- 0≦x≦1、0≦y≦1より
- 問2の正解の「y-x」は、-1≦y-x≦1の範囲を自由に動ける
- よって、問2の正解の「2cosθの値」によって△ACPの最小値は「場合分け」が発生する
これが解れば正解は目前です、頑張っていきましょう。
- (ⅰ)1<2cosθ すなわち 0<θ<π/3の時
- y-x=1で△ACP=\(\begin{aligned}\dfrac{1}{2} \sqrt{9-4\cos \theta -4\cos ^{2}\theta }\end{aligned}\)が最小値
- (ⅱ)-1≦2cosθ≦1 すなわち π/3≦θ≦2π/3の時
- y-x=2cosθで△ACP=√2sinθが最小値
- (ⅲ)2cosθ<-1 すなわち 2π/3<θ<πの時
- y-x=-1で△ACP=\(\begin{aligned}\dfrac{1}{2} \sqrt{9+4\cos \theta -4\cos ^{2}\theta }\end{aligned}\)が最小値
以上3つが正解です。
受験生としての解説
問1に関して、内積を使った三角形の面積公式ですが、不合格者さんの一定数が証明できません。合格者さんは証明できるので、合否を分ける1問より少し簡単な問題です。
問2に関して、角度θが鈍角なのでsinθ・cosθを使った「→AP」の表し方が難しくなっています。よって、不合格者さんには厳しく、合格者は正解してくるので、合否を分ける1問です。
問3に関して、正解が「場合分け」になっていると気付く事が難しいです。医学科の合否を分ける難問です。
- 計算:★★★★★(難しい)
- 閃き:★★★★(やや難しい)
- 知識:★★★(普通)
- 総合:★★★★(やや難しい)
- 短評:問1・問2が解けるなら選択するのはアリ
おわりに
私は、私の指導を受けてくださる生徒さんに
- 九州大学は「基礎」を反復すれば合格できる
- 「基礎の反復」は誰でもできる
日本は技術立国で、日本人なら誰でも「手に職をつける才能」を持っているから
- 「頭の良さ」で勝負せず
- 手に職をつけて九大合格しなさい
と言って、基礎の反復を要求します。
「基礎の反復」という楽ではない作業に「誰でもできる」という言葉をつける時、私はいつも罪悪感を感じます。
でも、生徒さんの未来がかかっているので、必ず言うようにしています。
生徒さんに「基礎の反復」を要求する以上、指導者の私は、少なくともそれ以上の負荷に耐えて見せねばなりません。
これからも、量だけは負けないよう
- 九州大学の過去問を研究し
- 戸畑高校で落ちこぼれるほどの「才能の無さ」を逆用して
誰でも九州大学に合格できる「九州大学の攻略法」を作っていく所存です。



