九州大学の物理過去問を1980~2023年まで43年分研究しました。
2005~2023年まで九大物理19年分を公開します。
各小問ごとの解説に加え、高校偏差値60前後の高校で落ちこぼれて
- 1番簡単な国立大学を目指せない
- 九州工業大学・熊本大学など想像もできない
などの学生さんが九大合格できる所まで簡略化した「点数の取り方」を公開します。
偏差値60前後の高校
| 高校 偏差値 | 6学区 | 5学区 | 4学区 | 3学区 | 2学区 |
|---|---|---|---|---|---|
| 63 | 春日 | 香住丘 | |||
| 62 | 福岡中央 | ||||
| 61 | 筑紫 | 宗像 | |||
| 60 | 筑前 | 新宮 | 八幡 | 戸畑 | |
| 59 | 筑紫中央 | ||||
| 58 | |||||
| 57 | 北筑 | 小倉西 | |||
| 56 | 香椎 |


- 九州大学の物理2023年・令和5年度
- 九州大学の物理2022年・令和4年度
- 九州大学の物理2021年・令和3年度
- 九州大学の物理2020年・令和2年度
- 九州大学の物理2019年・平成31年度
- 九州大学の物理2018年・平成30年度
- 九州大学の物理2017年・平成29年度
- 九州大学の物理2016年・平成28年度
- 九州大学の物理2015年・平成27年度
- 九州大学の物理2014年・平成26年度
- 九州大学の物理2013年・平成25年度
- 九州大学の物理2012年・平成24年度
- 九州大学の物理2010年・平成22年度
- 九州大学の物理2009年・平成21年度
- 九州大学の物理2008年・平成20年度
- 九州大学の物理2007年・平成19年度
- 九州大学の物理2006年・平成18年度
- 九州大学の物理2005年・平成17年度
- おわりに
九州大学の物理2023年・令和5年度
大問1
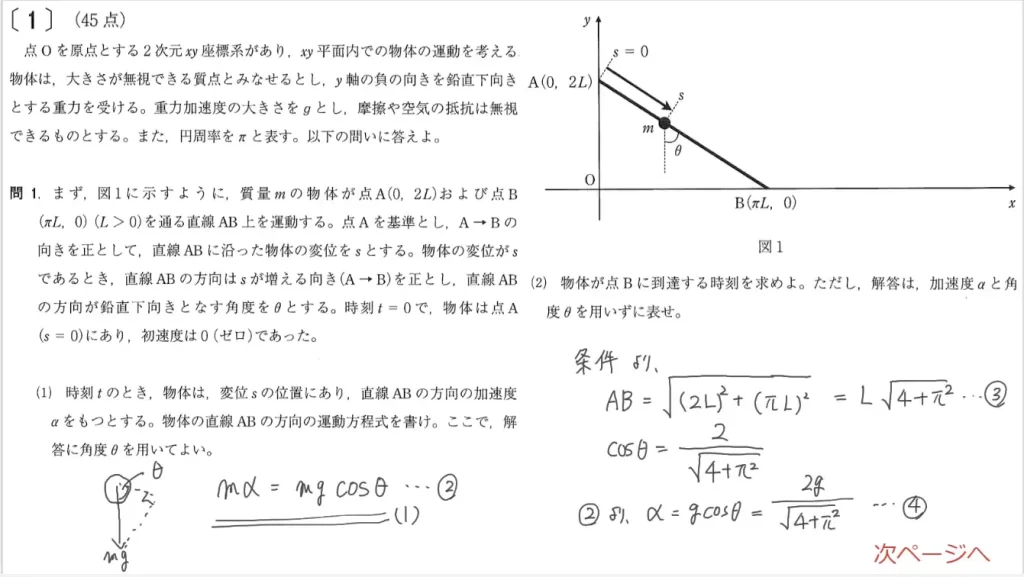
問1(1)に関して、物体の「直線AB方向の運動方程式」を答えます。
ポイントは「全ての力をAB方向へ換算すること」です。
- 物体が受ける重力のAB方向成分はmgcosθなので
- 運動方程式は
mα=mgcosθ…②(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、物体が「点Bに到達する時刻」を答えます。
ポイントは「等加速度直線運動」です。
- 条件より
AB=L√(4+π²)…③
cosθ=2/√(4+π²) - ②より
α=gcosθ
=2g/√(4+π²)…④ - 求める時刻t₀として
等加速度直線運動の公式より
1/2・αt₀²=AB…⑤ - ③④⑤より
t₀=√{L/g(4+π²)}(∵ t₀>0)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(1)に関して、ここでシチュエーションが変わります。物体の「曲線ABCの接線方向の運動方程式」を答えます。
- mβ=mgcosθ(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、物体が受ける力を変位sで表します。
ポイントは「問題文の①式」です。
①式を変形させるとcosθが求まります。
- ①より
cosθ=1-s/4L - (1)より、物体が受ける力はmgcosθなので
mgcosθ
=mg(1-s/4L)(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、物体の「往復運動の周期」を答えます。
ポイントは「運動方程式」です。
- (1)(2)より、物体の運動方程式は
mβ=mg(1-s/4L)
∴ β=g(1-s/4L)
=-g/4L・(s-4L) - 上式より、物体の運動は
振動中心:s=4L
角振動数:ω=√(g/4L)
の単振動とわかる - ゆえに周期Tとして
T=2π/ω
=4π√(L/g)(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(4)に関して、物体が曲線ABCに沿って点Bに到達する時と、点Aから点Bへ直線運動で到達する時の「時間の比率」を答えます。
- 点Aから点Bへ到達する時間は、問1より
t₀=√{L/g(4+π²)} - 曲線ABCに沿って点Bに到達する時間t₁は、問2(3)より
t₁=T/4
=π√(L/g) - よって、求める値は
t₁/t₀=π/√(4+π²) 倍
(これが正解です)
本問に参加するには、問2(3)の正解が必要です。
よって、問2(3)とセットで、合否を分ける1問より少し簡単な問題です。
問2(5)に関して、物体が点Bに「初めて到達する時の速さ」を答えます。
ポイントは「力学的エネルギー保存則」です。
- 力学的エネルギー保存則より
1/2・mv₀²=mg・2L
∴ v₀=2√(gL)
(これが正解です)
不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問3(1)に関して、ここでシチュエーションが変わります。2つの物体が「衝突する時刻」を答えます。
- 質量2mの物体の、曲線ABCの接線方向の運動方程式は
加速度γとして
2mγ=2mgcosθ
∴ γ=-g/4L・(s-4L) - 上式より、質量2mの物体の運動は
振動中心:s=4L
角振動数:ω’=√(g/4L)
周期:T’=2π/ω’=4π√(L/g)
の単振動とわかる - よって、2つの物体は点Bで衝突するため
求める時刻はt=t₁であり
問2(4)より
t₁=π√(L/g)
(これが正解です)
不合格者さんには難しく、合格者さんは正解してきます。
よって、合否を分ける1問です。
問3(2)に関して、点Bで合体した物体が到達する「最高点のy座標」を答えます。
ポイントは「合体後の速度を求めること」です。
合体後の速度が判れば、力学的エネルギー保存則で最高点を得られます。
- 質量2mの物体の
衝突直前の速さをv₁とおくと
力学的エネルギー保存則より
1/2・2mv₁²=2mgL
∴ v₁=√(2gL) - sが増加する方向を正として
衝突直後に一体となった物体の速度をv₂とおくと
運動量保存則より
mv₀+(-2mv₁)=3mv₂
∴ v₂=-2/3・(√2-1)√(gL) - よって、一体となった物体の
最高点のy座標をh’とおくと
力学的エネルギー保存則より
1/2・3mv₂²=3mgh’
∴ h’=2/9・(√2-1)²L
(これが正解です)
合格者さんでも一定数の不正解が出るレベルです。
よって、正解できれば他者に差をつける1問です。
大問3

問1(ア)に関して、気体分子がピストンに衝突した後の「速度のx成分」を答えます。
ポイントは「はね返りの式」です。
気体分子とピストンは弾性衝突するので、はね返りの式を使います。
- ピストンに衝突後の気体分子に関して
速度のx成分をvₓ’とおくと
はねかえりの式より
vₓ’-v₀=-(-vₓ-v₀)
∴ vₓ’=vₓ+2v₀
(赤部分が正解です)
不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問1(イ)に関して、ピストンと複数回衝突した後の「速度のx成分」を答えます。
ポイントは「(ア)の活用」です。
先程の(ア)で衝突後の速度のx成分を求めたので「衝突1回の速度の増加量」が判明しています。後は、衝突回数をかければ正解です。
- (ア)より
ピストンと1回衝突するごとに
速度のx成分が+2v₀される - 今、衝突回数はΔxvₓ/(2v₀L)回なので
求める値は
vₓ+2v₀・Δxvₓ/(2v₀L)
=(1+Δx/L)vₓ
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(ウ)に関して、ピストンOを止めた直後の気体分子について「速度のx成分の2乗の平均」を答えます。
ポイントは「速度のy成分・z成分」です。
問題文に「x軸に垂直で、直行する2方向」と書いてありますが、これがy・z成分です。(イ)より、速度のx成分はy・z成分の(1+Δx/L)倍と判っています。
以下、平均を表す「 ̄」を「*」で書きます。
- 問題文より、ピストンに衝突する前の
気体分子の速度のx成分の2乗の平均は
vₓ²=v²*/3
と書ける - これと(イ)より
衝突後は以下の様に書ける
(1+Δx/L)²×v²*/3
≒(1+2Δx/L)×v²*/3
(赤部分が正解です)
不合格者さんの一定数が不正解になるレベルです。
合否を分ける1問より少し簡単な問題です。
問1(エ)に関して、容器内部のN個の気体分子が持つ「運動エネルギーの増加量」を答えます。
ポイントは「変化=後-前」です。
問われているのは増加量(=変化量)なので、運動エネルギーを「圧縮前-圧縮後」で計算すればよいです。
- (ウ)より
ピストンとの衝突による
気体分子の速度のx成分の
2乗の平均の増加量は
変化量(=後-前)
=(1+2Δx/L)×v²*/3-v²*/3
=2Δx/3L × v²* - よって
N個の分子における
運動エネルギーの増加量は
m/2 × 2Δx/3L × v²* × N
=NmΔx/3L × v²*
(赤部分が正解です)
本問自体は不合格者さんでも正解してくるレベルです。
しかし、本問に参加するには(ウ)の正解が必要です。
よって、(ウ)とセットで、合否を分ける1問より少し簡単な問題です。
問1(オ)(カ)に関して、問題文の①式の左辺について「圧縮前後の変化量」をS,P,Lを用いて表します。
ポイントは「問題文に素直に従うこと」です。
問題文で①の関係式が与えられているため、落ち着いてこの式に当てはめれば正解できます。
| 圧力 | 体積 | |
|---|---|---|
| 圧縮前 | P | SL |
| 圧縮後 | P+ΔP | S(L-Δx) |
- 上の表を用いて
式①の左辺の変化量を書くと - 変化量(=後-前)
=(P+ΔP)S(L-Δx)-PSL
=-PSΔx+ΔPSL+ΔPSΔx
≒SL×ΔP-PS×Δx
(赤部分が正解です)
不合格者さんの一定数が不正解になるレベルです。
合否を分ける1問より少し簡単な問題です。
問1(キ)に関して、(カ)までの情報をまとめ「式②の形に整形」する問題です。
ポイントは「(オ)(カ)が左辺、(エ)が右辺に関係している」ことです。
- (エ)(オ)(カ)より
①式は以下の様に表せる
SLΔP-PSΔx=2/3 × NmΔx/3L × v²*
∴ SLΔP=(PS+2Nmv²*/9L)×Δx
∴ ΔP/P=(1+2Nmv²*/9SLP)×Δx/L…③ - また、圧縮前の状態に関して
①式は以下の様に表せる
PSL=2/3 ×1/2・Nmv²*
∴ Nmv²*=3SLP…④ - ③④より
ΔP/P=5/3・Δx/L
(これが正解です)
合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し難しい問題です。
問2(ク)に関して、ここでシチュエーションが変わります。ピストンnに「加わる力」を答えます。
ポイントは「ピストンnの左右の圧力」です。
ピストンは右に変位しているので、ピストンにかかる力は「左側の力-右側の力」で表せます。
- ピストンnの左側にかかる力は
(P+ΔPn-1)S
ピストンnの右側にかかる力は
(P+ΔPn)S - ゆえにピストンnに加わる力は
(P+ΔPn-1)S-(P+ΔPn)S
=(ΔPn-1-ΔPn)S
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
合否を分ける1問より少し簡単な問題です。
問2(ケ)に関して、ピストンnと共に運動する気体の「運動方程式」を答えます。
ポイントは「ピストンnと共に運動する」という文言です。
つまり、求めるべきN個の気体には(ΔPn-1-ΔPn)Sの力が加わります。これで運動方程式の右辺が見えました。
- 問題文の式
ΔPn/P=-γ(xn+1-xn)/L
より
ΔP=-γP(xn+1-xn)/L…⑤ - N個の気体分子に関する運動方程式より
Nman=(ΔPn-1-ΔPn)S
={-γP/L・(xn-xn-1)+γP/L・(xn+1-xn)}S(∵⑤)
=γPS/L・(xn+1-2xn+xn-1)…⑥
(赤部分が正解です)
N個の気体分子にかかる力が(ク)の正解、と気づく部分が少し難しいです。
問題文の長さと言い回しを考慮すると、不合格者さんには難しいです。
合格者さんは乗り越えてくるレベルなので、合否を分ける1問です。
問2(コ)に関して、(ケ)の運動方程式・右辺における(xn+1-2xn+xn-1)を「三角関数へ式変形」する問題です。
ポイントは、問題文「xn=Asin(ωt-2πnL/λ)」です。
自分で考えるのではなく、問題文を流用する問題とわかります。
- xn=Asin(ωt-2πnL/λ) より
- xn+1=Asin{(ωt-2πnL/λ)-2πL/λ}
=A{sin(ωt-2πnL/λ)cos2πL/λ-cos(ωt-2πnL/λ)sin2πL/λ} - xn-1=Asin{(ωt-2πnL/λ)+2πL/λ}
=A{sin(ωt-2πnL/λ)cos2πL/λ+cos(ωt-2πnL/λ)sin2πL/λ} - よって
xn+1-2xn+xn-1
=(xn+1+xn-1)-2xn
=2Asin(ωt-2πnL/λ)cos2πL/λ-2Asin(ωt-2πnL/λ)
=2×(cos2πL/λ-1)×xn…⑦
(赤部分がコの正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(サ)に関して、気体中を伝播する「音波の速さ」を答えます。
- ⑥⑦と問題文の近似式より
Nman=-4γPS/L・sin²(πL/λ)・xn
≒-4γPS/L・(πL/λ)²・xn
∴ an=-4γPS/LNm・(πL/λ)²・xn - 上式より
この単振動の角振動数をω’とおくと
ω’=√{4γPS/NmL・(πL/λ)²} - 音波の周波数をfとおくと
f=ω’/2π
=1/λ・√(γPSL/Nm) - よって、求める音波の速度vは
v=fλ
=√(γPSL/Nm)
(これが正解です)
合格者さんでも一定数の不正解が出るレベルです。
よって、合否を分ける1問より少し難しい問題です。
九州大学の物理2022年・令和4年度
大問1

問1(1)に関して、人工衛星が受ける「万有引力のx成分とy成分の大きさ」を答えます。
- 人工衛星が受ける
万有引力の大きさをFGとおくと
FG=GMm/r² - 図1において
人工衛星と原点をつなぐ直線が
x軸となす角をθとおくと
万有引力のx成分・y成分は
Fx=-FGcosθ=-FGx₁/r
Fy=-FGsinθ=-FGy₁/r - よって
|Fx|=GMmx₁/r³
(これが正解です)
|Fy|=GMmy₁/r³
(これが正解です)
不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問1(2)に関して、人工衛星が位置(r,0)にある時の速度→v₁、それから時間Δtの間に角度Δθだけ回転した時の速度→v₂の「x成分とy成分」を答えます。
ポイントは「rΔθ=vΔt」という関係です。
よって「Δθ=vΔt/r」と表すことができます。
- →v₁に関して
v₁x=0(これが正解です)
v₁y=v(これが正解です) - →v₂に関して
v₂x=-vsinΔθ=-vsin(vΔt/r)
(これが正解です)
v₂y=vcosΔθ=vcos(vΔt/r)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
合否を分ける1問より少し簡単な問題です。
問1(3)に関して、(2)における速度変化を答えます。
ポイントは「変化=後-前」です。
- Δvx=v₂x-v₁x=-vsin(vΔt/r)
(これが正解です。)
Δvy=v₂y-v₁y=v{cos(vΔt/r)-1}
(これが正解です)
基本の流れが続きます。
本問に参加するには問1(2)の正解が必要です。
よって、問1(2)とセットで、合否を分ける1問より少し簡単な問題です。
問1(4)に関して、人工衛星が(r,0)の位置にある時の「加速度のx成分とy成分」を答えます。
ポイントは「加速度=速度÷時間」です。
- ax=Δvx/Δt
=-v/Δt・sin(vΔt/r)
=-v/Δt・sinΔθ
≒-v/Δt・vΔt/r
=-v²/r(これが正解です) - ay=Δvy/Δt
=v/Δt・{cos(vΔt/r)-1}
=v/Δt・(cosΔθ-1)
≒v/Δt・(1-1)
=0(これが正解です)
基本の流れが続きます。
本問に参加するには問1(3)の正解が必要です。
よって、問1(3)とセットで、合否を分ける1問より少し簡単な問題です。
問1(5)に関して、人工衛星の軌道半径rを答えます。
ポイントは「人工衛星の速度」です。
「rを求めよ」という問題なので、運動方程式「mv²/r=GMm/r²」を使うことは想像がつきます。この式から速度vを消せれば正解できそうです。
- 人工衛星は時間Tの間に
距離2πrを移動するので
その速度vは
v=2πr/T - 人工衛星の向心方向の運動方程式より
mv²/r=GMm/r²
∴ 4mπ²r/T²=GMm/r²
∴ r=³√(GMT²/4π²)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(1)に関して、ここでシチュエーションが変わります。人工衛星が楕円軌道になります。人工衛星の地球向きと垂直な方向の速度成分を答えます。
ポイントは「素直に立式すること」です。
sinΦを使って速度成分を表現すれば、問題文で面積速度hが与えられているので正解につなぐことができます。
- v⊥=vsinθ
=2h/r(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、人工衛星の万有引力による位置ネルギーUを答えます。
- U=-∫-GMm/R₂ dR(積分区間は∞→r)
=-[GMm/R]
=-GMm/r
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、人工衛星の力学的エネルギーを答えます。
ポイントは「v∥を使って答えること」です。
vをそのまま使えないのでcosΦを経由します。
- 図より
v∥=vcosΦ
∴ cosΦ=v∥/v - sin²Φ+cos²Φ=1より
(2h/rv)²+(v∥/v)²=1
∴ v²=v∥²+4h²/r² - 人工衛星の力学的エネルギーEに関して
E=mv²/2-GMm/r
=m/2・(v∥²+4h²/r²)-GMm/r
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(4)に関して、問題文で定義されたV(r)に関して「V(r)=0」となるrおよび「V(r)のグラフ」を答えます。
- 問3の結果からv∥の項を省くと
V(r)=2mh²/r²-GMm/r
となる - V(r)=2mh²/r²-GMm/r=0
の時r=rcなので
rc=2h²/GM
(これが正解です)
グラフに関して
- 0<r<rcの時、V(r)>0
- rc<rにおいてV(r)<0
- r→∞でV(r)→0
なので上記を作図したものが正解です。
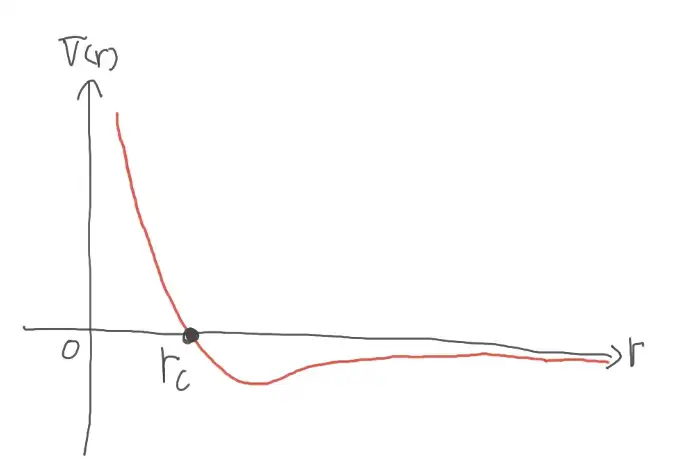
計算は普通レベルです。
しかし、本問に参加するには、問2(3)の正解が必要です。
よって、問2(3)とセットで、合否を分ける1問です。
問3(1)に関して、ここでシチュエーションが変わります。図の様に地表面から発射した瞬間の、人工衛星の力学的エネルギーを答えます。
| 運動エネルギー | 1/2・mv₀² |
| 位置エネルギー | -GMm/R |
- E₀=1/2・mv₀²-GMm/R
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問3(2)に関して、人工衛星が無限遠方に届くために必要な「最小の初速vmin」を答えます。
ポイントは「無限遠方における力学的エネルギー」です。
無限遠方では位置エネルギー=0となるため、この時点で「力学的エネルギー≧0」ならば無限遠方に飛んでいきます。
- 無限遠方に飛んでいく条件はE₀≧0
∴ v₀≧√(2GM/R) - よって
vmin=√(2GM/R)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
大問2

問1(1)に関して、コイルが静止している時、コイルに流れる電流の大きさI₀を答えます。
- オームの法則よりE=I₀R
∴ I₀=E/R(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、コイルをθ回転させた時、コイルの4辺が磁場から受ける力の向きを答えます。
ポイントは「左手の法則」です。
- 左手の法則より正解は(e)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(3)に関して、コイルの4辺が磁場から受ける「y軸まわりの力のモーメントの和」N(θ)を答えます。
ポイントは「辺C₂C₃、辺C₄C₁の力のモーメントは0」であることです。
辺C₁C₂・辺C₃C₄に関して計算していきましょう。
- 辺C₁C₂・辺C₃C₄が
磁場から受ける力のモーメントの
腕の長さはasinθなので
N(θ)=2(-2I₀Ba・asinθ)
=-4EBa²sinθ/R
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(4)に関して、N(θ)=0となる2つの回転角θ₁・θ₂(θ₁<θ₂)を答えます。
- N(θ)=0となるのはsinθ=0の時なので
θ₁=0,θ₂=π
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、ここでシチュエーションが変わります。志賀さんと能古さんの会話中(ア)~(オ)を答えます。
- θ₁=0<θ<π=θ₂において
sinθ>0なので
N(θ)=-4EBa²sinθ/R<0
となる - そして、ΔW=-N(θ)Δθとかけるので
ΔWとΔθは「ア:同」符号の関係になる。
(これが正解です) - また、-π/2≦θ<θ₁=0とπ=θ₂<θ<3π/2の範囲では
sinθ<0より
N(θ)>0なので
ΔWとΔθは常に「イ:異」符号の関係になる。
(これが正解です) - すると状態1(θ=0)からθを変化させる時
コイルにする仕事の符号は必ず「ウ:正」で
状態2(θ=π)から変化させる時は
コイルにする仕事の符号は必ず「エ:負」になる。
(これが正解です) - ゆえに、どちらの状態でもN(θ)=0であるが
コイルの回転角θが少し変化しても
元に戻ろうとする『安定』な状態なのは
状態「オ:1」の方となる。
(これが正解です)
(オ)に関して。
- N(θ)=-4EBa²sinθ/R
- ΔW=-N(θ)Δθ
上2式より、θを0→Δθと動かすと、コイルが磁場から受ける力Nの符号はマイナスである事に対し、仕事ΔWの符号はプラスとなります。
つまり、かけた力と反対方向にローレンツ力を受けるため『安定』となっています。
(ア)(イ)は不合格者さんでも正解してくるレベルです。
(ウ)(エ)は不合格者さんの一定数が不正解になるレベル。
(オ)は不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
問2(4)に関して、コイルを貫く磁束の単位時間あたりの変化を答えます。
ポイントは「変化量=後-前」です。
変化前・変化後の状態を丁寧に考え、引き算しましょう。
- ΔΦ(t)=Φ(t+Δt)-Φ(t)
=4a²B{cos(θ+Δθ)-cosθ}
=4a²B(cosθcosΔθ-sinθsinΔθ-cosθ)
≒4a²B(cosθ-Δθsinθ-cosθ)
=-4a²BΔθsinθ
=-4a²BωΔtsinωt - よって
ΔΦ(t)/Δt=-4a²Bωsinωt
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(5)に関して、時間tにコイルを流れる電流I(t)を答えます。
ポイントは「キルヒホッフの第2法則」です。
【キルヒホッフの第2法則】
任意の閉回路を一定方向に辿った時、電圧の総和は0になる
- I(t)R+ΔΦ(t)/Δt=E
∴ I(t)=(E+4a²Bωsinωt)/R
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(6)に関して、志賀さん能古さんの会話に出てきた「十分ゆっくりコイルを回す時」と、(4)以降の「角速度ωで回転させた時」の仕事量を比較します。更にその「理由」を答えます。
ポイントは「単位時間あたりにコイルを貫く磁束の変化量」です。
十分ゆっくり回した時より角速度ωで回した方が大きくなります。よって、誘導起電力が大きくなるため、誘導電流が大きくなり、それにより磁場から受けるローレンツ力も・・・という流れです。
| 正解 | W’>W₀ |
| 理由 | 単位時間あたりにコイルを貫く磁束の変化量が大きくなるため、誘導電流も大きくなり、ローレンツ力も大きくなる。ゆえに外力が大きくなるため、仕事も大きくなるから。(78文字) |
合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より難しい問題です。
大問3
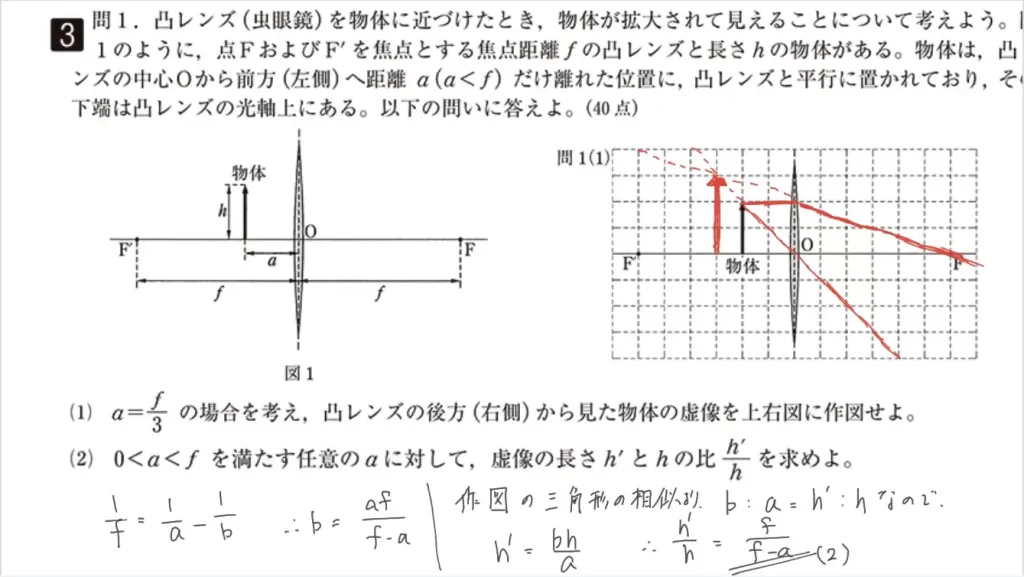
問1(1)に関して、作図問題です。凸レンズの後方(右側)から見た物体の虚像を作図します。
ポイントは「2つの光線」です。
- 物体の先端からレンズの真ん中を通る光線
- 物体の先端から地面と水平に進み、レンズで屈折して焦点を通る光線
2本の光線が交わる所に像の先端が来ます。よって
- レンズの中心Oから「左に3マス、上に3マス」を先端とした虚像
が正解です。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、虚像の長さh’と物体の長さhの比h’/hを答えます。
ポイントは「三角形の相似」です。
- 「物体の先端 → レンズの中心」を斜辺とする直角三角形
- 「虚像の先端 → レンズの中心」を斜辺とする直角三角形
2枚の三角形の相似比から正解が求まります。
- レンズの公式より
1/f=1/a-1/b
∴b=af/(f-a) - また、b:a=h’:hより
h’/h=b/a
=f/(f-a)(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(1)に関して、sinθ₁を答えます。
- h=rsinθ₁
∴ sinθ₁=h/r(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、点Pにおける屈折角θ₂とした時のsinθ₂を答えます。
- 屈折の法則より
1・sinθ₂=nsinθ₁
∴ sinθ₂=nsinθ₁
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、光線が全反射する時の条件を答えます。
ポイントは「全反射する=屈折角が90°」です。
- nsinθc=1・sinπ/2
∴ sinθc=1/n
(これが正解です) - 全反射条件は
θ₁>θc
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(4)に関して、ここでシチュエーションが変わります。sinθ≒θの近似が成り立つ世界において、平凸レンズを出て後方(右側)に進む光線と光軸のなす角θ₃を答えます。
ポイントは「θ₂=θ₁+θ₃」になっていることです。
図2において、点Pから水平右向きに補助線を引くと正解が見えます。
- (1)と近似より
θ₁≒sinθ₁=h/r - (2)と近似より
θ₂≒sinθ₂
=nsinθ₁
≒nθ₁
=nh/r - 今、θ₂=θ₁+θ₃なので
θ₃=θ₂-θ₁
=nh/r – h/r
=(n-1)h/r
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(5)に関して、図の「OF間の距離(焦点距離)f」を答えます。
ポイントは、問題文末尾「tanθ₃≒θ₃の近似が成り立つ」です。
tanθ₃を使う問題だと解ります。
- tanθ₃≒θ₃
=h/f - (4)の結果と合わせて
(n-1)h/r=h/f
∴ f=r/(n-1)
(これが正解です)
本問自体は難しくありません。
しかし、本問に参加するには問2(4)の正解が必要です。
よって、問2(4)とセットで、合否を分ける1問です。
問2(6)に関して、ここでシチュエーションが変わります。(5)まで使ってきた装置を、屈折率n’の液体中に置いた時の「焦点距離f’」を答えます。
- 屈折の法則より
nsinθ₁=n’sinθ₂
∴ sinθ₂=n/n’・sinθ₁ - sinθ₁≒θ₁=h/r
sinθ₂≒θ₂=n/n’・θ₁=nh/n’r
であり - θ₂=θ₁+θ₃より
θ₃=θ₂-θ₁
=nh/n’r-h/r - ここで
tanθ₃≒θ₃
f’tanθ₃=hより
f’=h/tanθ₃
=h/θ₃
=h/(nh/n’r-h/r)
=n’r/(n-n’)(これが正解です) - また
f’-f=n’r/(n-n’) - r/(n-1)
=n(n’-1)r/(n-n’)(n-1)>0
より
f’>f(これが正解です)
合格者さんでも一定数が不正解になるレベルです。
よって、合否を分ける1問より難しい問題です。
問3(1)に関して、ここでシチュエーションが変わります。光が薄膜とガラスの境界で反射する時の「位相のずれ」を答えます。n₂<n、n₂>nの2パターンに関して答えます。
- n₂<nの時
位相のずれはπ(これが正解です) - n₂>nの時
位相のずれは0(これが正解です)
付け足される形で「薄膜の反射」が出題されています。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3(2)に関して、薄膜の両面で反射した光が「弱め合う条件」を(a)n₂<nおよび(b)n₂>nの場合で答えます。
ポイントは「光路差と波長」です。
- (a)n₂<nの時
空気-薄膜間で反射される光の位相はπずれる
薄膜-ガラス間で反射される光の位相はπずれる
よって、反射された光の位相は等しくなる - 今、光路差は2n₂dなので
この長さが半波長の奇数倍となれば
2つの光は弱め合う、よって
2n₂d=(m+1/2)λ
(これが正解です) - (b)n₂>nの時
空気-薄膜間で反射される光の位相はπずれる
薄膜-ガラス間で反射される光の位相はずれない
よって、反射された光の位相はπずれている - 今、光路差は2n₂dなので
この長さが半波長の偶数倍となれば
2つの光は弱め合う、よって
d=0の場合を除外して
2n₂d=(m+1)λ
(これが正解です)
不合格者さんは正解できず、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
九州大学の物理2021年・令和3年度
大問1

問1(1)に関して、小球1が小球2を押す力の大きさをs₁を使って表します。
ポイントは「力のつり合い」です。
小球は静止しているので、力がつり合っています。
- 小球1の力のつり合いより
k₁s₁-F=0
∴ F=k₁s₁…①
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、s₁およびs₂の大きさを求めます。
ポイントは「バネの縮み=壁の移動距離」です。
- 小球2の力のつり合いより
-k₂s₂+F=0…② - また
s₁+s₂=D…③ - ①~③より
s₁=k₂D/(k₁+k₂)(これが正解です)
s₂=k₁D/(k₁+k₂)(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(1)に関して、手を放す直前のばね1の縮をDおよびdを用いて表します。
ポイントは「ばね2が自然長であること」です。
ばねが縮む要素は、全てばね1が背負っています。
- 壁の移動分D
小球間の距離d - これらを全てばね1が担っているので
D+d(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、小球2に衝突する直前の小球1の速度V₀を答えます。
ポイントは「力学的エネルギー保存則」です。
- 力学的エネルギー保存則より
k₁(D+d)²/2=k₁D²/2+m₁V₀²/2
∴ V₀=√{k₁d(2D+d)/m₁}…④
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、衝突直後の小球1と小球2の速度V₁V₂を使い、運動量保存則の式を書きます。
- m₁V₀=m₁V₁+m₂V₂…⑤
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(4)に関して、小球1・2の間の反発係数eをV₀V₁V₂を使って答えます。
ポイントは「はね返りの式」です。
- はね返りの式より
V₁-V₂=-e(V₀-0)
∴ e=-(V₁-V₂)/V₀…⑥
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(5)に関して、V₁とV₂をV₀で表します。
- ⑤⑥より
V₁=(m₁-em₂)V₀/(m₁+m₂)
(これが正解です)
V₂={(1+e)m₁}V₀/(m₁+m₂)
(これが正解です)
不合格者さんでも正解してくるレベルです。
よって、全ての受験生さんが正解したい問題です。
問2(6)に関して、衝突後の小球2の最大変位x₂を答えます。
ポイントは「力学的エネルギー保存則」です。
衝突によって小球2が得た運動エネルギーが、全てバネの弾性エネルギーに変わる点が、求める変位x₂となります。
- 力学的エネルギー保存則より
m₂V₂²/2=k₂x₂²/2
∴ x₂=V₂√(m₂/k₂)…⑦
(これが正解です)
不合格者さんでも正解してくるレベルです。
よって、全ての受験生さんが正解したい問題です。
問2(7)に関して、(6)の最大変位に達するまでの時間を答えます。
ポイントは「運動方程式」です。
ここまで主に保存則で正解してきましたが「時間を求めよ」という出題なので運動方程式です。
- 小球2のばねの自然長の位置をx=0とおく
- 小球2の運動方程式より
m₂a₂=-k₂x
∴ a₂=-k₂x/m₂ - 上式より小球2は
振動中心x=0
角振動数ω₂=√(k₂/m₂)
の単振動とわかる - 周期をT₂とすると
T₂=2π/ω₂
=2π√(m₂/k₂)…⑧ - 求める時間は1/4周期なので
T₂/4=π/2・√(m₂/k₂)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(8)に関して、「d=2D、m₁=m₂=m₀、k₁=4k₀、k₂=k₀、e=1」とした時の、時間tと小球1・2の変位のグラフを描きます。
ポイントは「V₁=0となること」です。
(5)の結果に(8)の条件(m₁=m₂、e=1)を代入すると「V₁=0」となります。よって、小球1の運動は「初速0、ばねの縮みD、角振動数ω₁の単振動」とわかります。小球2については、(7)までの問題で解析してあります。
- 小問(5)の結果と条件より
V₁=(m₀-m₀)V₀/(m₀+m₀)=0
V₂=(1+1)m₀V₀/(m₀+m₀)=V₀ - よって、小球1は
初速0
ばねの縮みD
から始まる単振動とわかる - また、小球2は
初速V₀
ばねは自然長
からの単振動とわかる - ④に与えられた条件を代入して
V₀=√{4k₀2D(2D+2D)/m₀}
=4D√(2k₀/m₀) - 振幅に関して
小球1の振幅は上記よりD - 小球2の振幅は(6)より
V₂√(m₂/k₂)
=V₀√(m₀/k₀)
=4√2・D - 小球1の周期は
T₁=2π/ω₁
=2π√m₀/k₀
=2T₀ - 小球2の周期は
T₂=2π/ω₂
=2π√m₀/k₀
=2T₀
上記をグラフに描いたものが正解です。
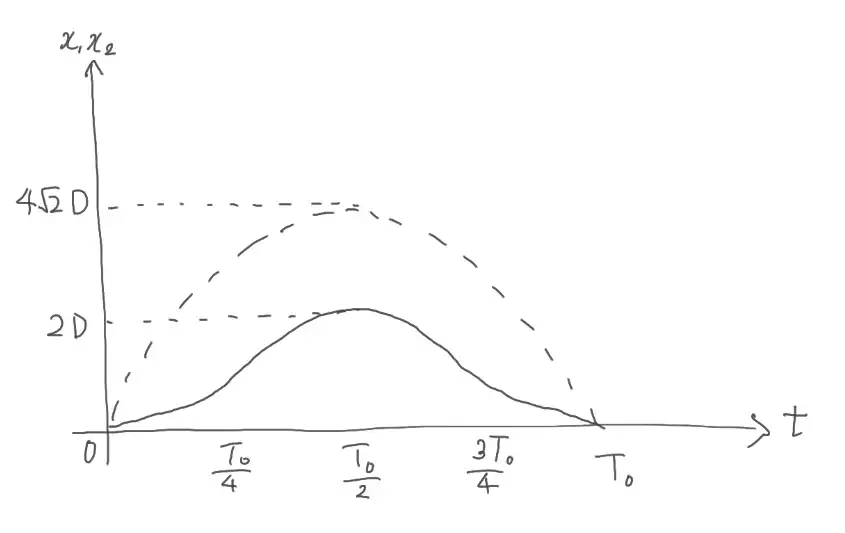
合格者さんでも一定数の不正解が出るレベルです。
よって、合否を分ける1問より難しい問題です。
大問2

問1(1)に関して、スイッチを閉じた直後に抵抗の両端にかかる電圧を答えます。
- スイッチを閉じた直後は
コンデンサーの電圧降下を無視できるので
抵抗の両端の電圧はV
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、十分に時間が経過した後、極板①に蓄えられている電気量Q、およびコンデンサーの静電エネルギーUを答えます。
ポイントは、問題文「十分に時間が経過」です。
コンデンサは充電され、回路に電流は流れていません。
- コンデンサーの電気容量をCとおくと
C=ε₀s/d - よって
Q=CV₀=ε₀sV/d
(これが正解です) - また
U=1/2・QV
=1/2・CV²
=ε₀sV²/2d
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(3)に関して、(2)までに電池のした仕事Wを答えます。
- W=QV(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(4)に関して、コンデンサーに蓄えられた静電エネルギーが「電池のした仕事より小さい理由」を25字以内で答えます。
「25字以内」という指定なので、80%の20字以上で解答してください。
- 抵抗で生じるジュール熱として消費されたから。
(22文字、これが正解例です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(5)に関して、抵抗に流れる電流の時間変化のグラフを描いて答えます。
ポイントは以下の3点です。
- グラフの始点が(0,V/R)であること
- 下に凸なグラフであること
- やがて電流が0になること
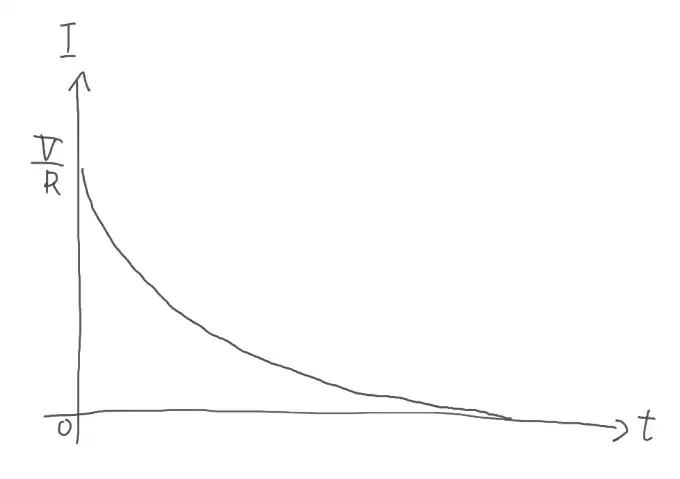
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(1)に関して、ここでシチェーションが変わります。荷電粒子Pが原点Oを通過する時の速さvを答えます。
粒子が電場から受けた仕事が、粒子の運動エネルギーに変わっている事を立式すれば正解できます。
- 電場の強さをEとすると
E=V/d - 粒子が電場から受ける力は
F=qE=qV/d - 粒子が電場からされる仕事は
W=F・d/2=qV/2 - これが粒子の運動エネルギーになっているので
1/2・Mv²=qV/2
∴ v=√(qV/M)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(2)に関して、図のx>0における「磁場の向き」を答えます。
ポイントは「左手の法則」です
- 正の電荷を持つ粒子が右向き:中指が右向き
- 受ける力は上向き:親指が上向き
- 結果として
人差し指(磁場の向き)は
紙面「表→裏」向き
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、荷電粒子Pが「等速円運動を行う理由」を30字程度で答えます。
「30字程度で答えよ」と書いてあるので32文字(80%)以上使ってください。できるだけ36文字(90%)以上にしてください。
- 荷電粒子の進行方向に対してローレンツ力が常に垂直にはたらき向心力となるから(37文字)
(これが正解例です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問2(4)に関して、磁場の影響で曲がった粒子がスクリーンに当たる座標を答えます。
ポイントは「原点Oが円運動の最下点になっていること」です。
よって「円運動の半径の2倍」が正解となります。
- 粒子Pの円運動の半径をrとすると
運動方程式より
Mv²/r=qvB
∴ r=Mv/qB - よって
Y=2r
=2Mv/qB
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(5)に関して、(4)の2倍の座標「y=2Y」で検出される荷電粒子を8択から全て答えます。
ポイントは「Mとqの関係」です。
- (5)より
Y=2Mv/qB
=2/B・√MV/q…① - これがY→2Yとなるのは
①のルート内が4倍になる時なので - これを満たすのは「bとf」
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
大問3

(1)に関して、TB/TA、TC/TA、TD/TAをGを用いて表します。
ポイントは「立てられる式を全て立てる事」です。
最初の問題から「TA、TB、TC、TD」を全て問われているので大変です。重厚な体勢で臨みます。
- 状態A~Dにおける状態方程式と
問題文で定義された断熱変化の関係より - pAVA=RTA…①
- pBVB=RTB…②
- pBVA=RTC…③
- pAVD=RTD…④
- TApA^-2/5=TBpB^-2/5…⑤
- TCpB^-2/5=TDpA^-2/5…⑥
準備が整いました。
①~⑥を組み合わせて正解を出していきます。
- ⑤より
TB/TA
=(pA/pB)^-2/5
=G^2/5
(これが正解です) - ③÷①より
TC/TA
=pB/pA
=G
(これが正解です) - ⑥÷⑤と②③と①②より
TD/TA
=TC/TB
=pBVA/pBVB
=TApB/TBpA
=G^3/5
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
(2)に関して、B→Cにおいて「気体が外部から吸収した熱量QBC」とRTAの比を、Gを使って答えます。
ポイントは「B→Cが定圧変化」である事です。
- QBC=5R/2・(TC-TB)より
- QBC/RTA
=5/2・(TC/TA-TB/TA)
=5/2・(G-G^2/5)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(3)に関して、C→Dにおいて「気体が外部にした仕事WCD」とRTAの比を、Gを使って答えます。
- C→Dにおける
内部エネルギー変化をUCDとおくと
熱力学第1法則より
WCD=UCD=3R/2・(TC-TD) - よって
WCD/RTA
=3/2・(TC/TA-TD/TA)
=3/2・(G-G^3/5)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(4)に関して、D→Aにおける「気体が外部に放出した熱量QDA」とRTAの比を、Gを使って答えます。
- QDA=5R/2・(TD-TA)
∴ QDA/RTA
=5/2・(TD/TA-TA/TA)
=5/2・(G^3/5 -1)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(5)に関して、A→B→C→D→Aの変化をTVグラフに作図します。
- pV=RTより
定圧変化のB→CとD→Aは
p=一定となるため
TとVの比例グラフとなる。 - また、問題文の
Tp^-2/5=一定に
p=RT/Vを代入すると
T^3/5・V^2/5=一定
となるので
A→BとC→Dは
下に凸なグラフとなる
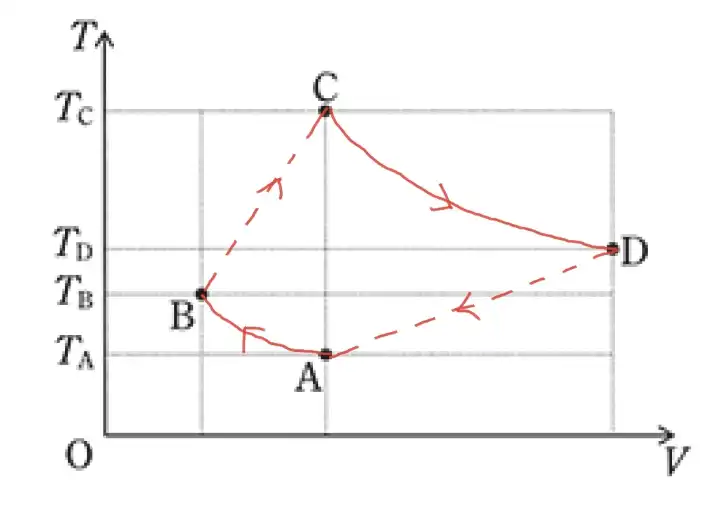
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(6)に関して、問題文の空所ア~エに入る式、a・bに入る数字を答えます。
- このサイクルの熱効率e₁に関して
e₁=(QBC-QDA)/QBC
=1-QDA/QBC(アの正解です)
=1-{5R/2・(TD-TA)}/{5R/2・(TC-TB)}
=1-(TD-TA)/(TC-TB)(イ・ウの正解です)
=1-(TD/TA-1)/(TC/TA-TB/TA)
=1-(G^3/5-1)/(G-G^2/5)
=1-G^-2/5(aの正解です) - e₂={QBC-QR-(QDA-QR)}/(QBC-QR)
=1-(QDA-QR)/(QBC-QR) - ここで
QR=5R/2{TD-(TD+TB)/2}
=5R/4・(TD-TB)
より - e₂=1-{5R/2・(TD-TA)-5R/4・(TD-TB)}/{5R/2・(TC-TB)-5R/4・(TD-TB)}
=1-(TD-2TA+TB)/(2TC-TB-TD)
=1-{(TD-TA)+(TB-TA)}/{(TC-TB)+(TC-TD)}
(以上より「TB-TA」がエの正解です) - よって
e₂-e₁
=(TC-TD)/(TC-TB+TC-TD)・{G^-2/5-(TB-TA)/(TC-TD)} - ここで
(TB-TA)/(TC-TD)を
Gを用いて表すと
(TB-TA)/(TC-TD)
=(TB/TA-1)/(TC/TA-TD/TA)
=(G^2/5-1)/(G-G^3/5)
=G^-3/5
(これがbの正解です)
(ア)~(ウ)と(a)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(エ)と(b)
合格者さんでも一定数の不正解が出るレベルです。
よって、合否を分ける1問より難しい問題です。
九州大学の物理2020年・令和2年度
大問1

問1(1)に関して、台と物体を一体として考えた時の「運動方程式」を答えます。
- 台と物体を一体として考えた時
運動方程式より
(M+m)a=-kx
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(2)に関して、この単振動の「周期T₀」を答えます。
- 問1(1)の結果より
a=-kx/(M+m) - ゆえにこの運動は
振動中心:x=0
角振動数:ω=√{k/(M+m)}
の単振動である - よって
T₀=2π/ω
=2π√{(M+m)/k}
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(3)に関して、物体が台から受ける「摩擦力」および、台が物体から受ける「摩擦力」を答えます。
ポイントは「作用反作用の法則」です。
台と物体には同じ大きさの摩擦力が反対方向にかかります。
- 物体が台から受ける摩擦力は
maに等しいので
ma=-mkx/(M+m)
(アの正解です) - また、作用反作用の法則より
台が物体から受ける摩擦力は
-ma=mkx/(M+m)
(イの正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(4)に関して、台と物体が常に一体となって運動するための「最大の振幅」を求めます。
ポイントは最大摩擦力「μN=μmg」です。
- 求める最大の振幅をx₀とおくと
-mkx₀/(M+m)=-μmg
∴ x₀=μ(M+m)g/k
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(1)に関して、ここからシチュエーションが変わります。問1(4)の最大振幅を超えて運動させた時の「台と物体の運動方程式」を答えます。
- 台:Ma₁=-kx+μ’mg
(これが正解です) - 物体:ma₂=-μ’mg
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、時刻tにおける「物体の速度」を求めます。
ポイントは「速度=加速度×時間+初速」です。
- 問2(1)の結果より
a₂=-μ’g - 求める物体の速度をvとして
v=a₂t
=-μ’gt
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、単振動する台の「振幅」と「周期T₁」を答えます。
ポイントは「台の運動方程式」です。
問2(1)の正解を活用します。
- 問2(1)の結果より
a₁=-k/M(x-μ’mg/k) - よって、この運動は
角振動数:Ω=√(k/M)
振動中心:x=μ’mg/k
の単振動である - よって
T₁=2π/Ω
=2π√(M/k)
(これが正解です) - また、振幅は
A-μ’mg/k
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(4)に関して、時刻t=T₁/4における台の速度を答えます。
ポイントは「単振動を三角関数で表す」ことです。
- 台の速度をV(t)とおくと
V(t)=-(A-μ’mg/k)√(k/M)・sin√(k/M)t - ここで
t=T₁/4=π/2・√(M/k)の時
V(T₁/4)=-(A-μ’mg/k)√(k/M)・sinπ/2
=-(A-μ’mg/k)√(k/M)
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(5)に関して、ここでシチュエーションが変わります。t=T₁/4で台と物体が同じ速度になった時の「t=0~T₁/4までの台と物体の速度のグラフ」を答えます。
ポイントは「t=T₁/4で速度が等しくなる事」です。よって、下記3点を満たすグラフを描けば正解です。
- 2つのグラフの「始点と終点」は同じ
- 単振動する台はサインカーブ(-sinカーブ)
- (2)より物体は等加速度運動なので、グラフは直線

本問自体は難しくありません。
しかし、本問に参加するには問2(4)の正解が必要です。
よって問2(4)とセットで、合否を分ける1問です。
問2(6)に関して、「バネの伸びA」を答えます。
ポイントは「t=T₁/4において、台と物体の速度が等しくなること」です。
- t=T₁/4において
台と物体の速度が等しくなるので
問2(2)より
-μ’gT₁/4=V(T₁/4)
∴-πμ’g/2・√M/k=-(A-μ’mg/k)√k/M
∴A=μ’g/k(πM/2 + m)
(これが正解です)
本問自体は難しくありません。
しかし、本問に参加するには問2(4)の正解が必要です。
よって問2(4)とセットで、合否を分ける1問です。
問(7)に関して、台と物体が一体となった時の「ばねの縮みB」を答えます。
ポイントは「力学的エネルギー保存則」です。
t=T₁/4で台と物体が合体した瞬間の力学的エネルギーと、縮みBの時の力学的エネルギーが保存します。
- t=T₁におけるバネの伸びは
μ’mg/k - 速度は(6)より
-πμ’g/2・√M/k - よって
力学的エネルギー保存則より
kB²/2=(M+m)/2・(-πμ’g/2・√M/k)²+k/2(μ’mg/k)²
∴ B=μ’g/k・√{π²M(M+m)/4+m²}
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
大問2

(1)に関して、極板Aに蓄えられている「電気量」を答えます。
- 求める電気量をQ₁とおくと
Q₁=CV₀
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(2)に関して、コンデンサーに蓄えられている「静電エネルギー」を答えます。
- 求める静電エネルギーをU₁とおくと
U₁=1/2・CV₀²
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(3)に関して、ここからシチュエーションが変わります。幅d/2の誘電体をコンデンサー内に挿入します。この時の「極板Aに蓄えられている電気量」を答えます。
ポイントは「コンデンサの直列」です。
- 誘電体が入ってない部分C₁
- 誘電体が入っている部分C₂
2つのコンデンサーが直列になっているとみなす事です。
- 誘電体が入ってない部分C₁
誘電体が入った部分C₂
2つのコンデンサの直列つなぎとみなす - C₁・C₂の電気容量は
C₁=2C
C₂=4C - 極板Aに蓄えられている
電気量をQ₂とおくと
2つのコンデンサーの極板間の
電位差をV₁・V₂として
Q₂=C₁V₁・・・①
Q₂=C₂V₂・・・②
V₁+V₂=V₀・・・③ - ①~③より
Q₂/C₁+Q₂/C₂=V₀
∴Q₂=4CV₀/3
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(4)に関して、極板間の電場と電位を「グラフ」に作図します。
ポイントは、問題文「電場は上向きを正とする」です。
本問の電場は下向きなので、グラフに書く際はマイナスをつける必要があります。
- C₁・C₂部分の電場をE₁・E₂とすると
E₁=-V₁/d/2=-4V₀/3d
E₂=-V₂/d/2=-2V₀/3d - また、極板Bからd/2における電位は
|E₂|×d/2=V₀/3 - よって
正解のグラフは以下のとおり
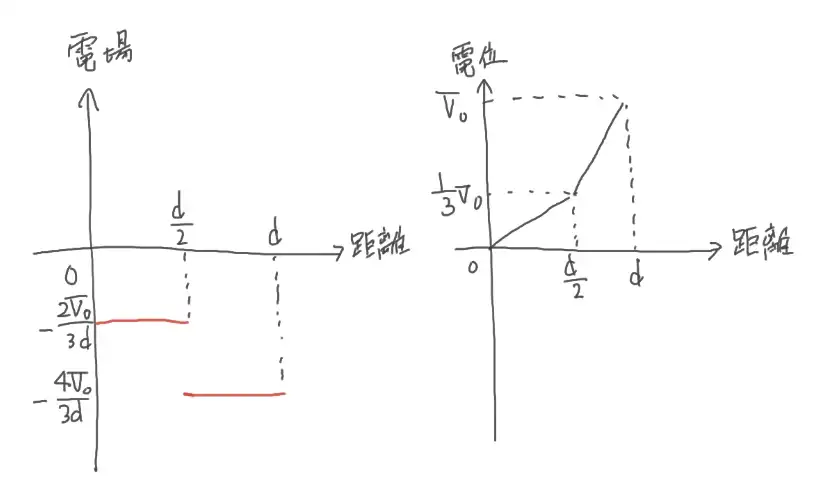
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(5)に関して、誘電体を挟む前後における「静電エネルギーの増加量、電池のした仕事、および外力のした仕事」を求めます。
ポイントは「簡単な順に求めること」です。
静電エネルギーの変化は、現在判っていることですぐ求まります。電池のした仕事も同様です。この2者の差をとることで「外力のした仕事」が求まります。
- 誘電体を差し込んだ後の静電エネルギーをU₂とおくと
U₂=Q₂V₀/2=2CV₀²/3 - ゆえに静電エネルギーの増加量は
U₂-U₁=CV₀²/6
(これが正解です) - また電池のした仕事をWとおくと
W=(Q₂-Q₁)V₀
=CV₀²/3
(これが正解です) - よって
外力のした仕事wとおくと
w=ΔU-W
=-CV₀²/6
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(6)に関して、ここでシチュエーションが変わります。極板Aを下に動かし誘電体と接触させ、その後スイッチSを開いた時の「極板Aに蓄えられている電気量、コンデンサーに蓄えられている静電エネルギー」を答えます。
ポイントは、問題文の「その後、スイッチSを開放した」です。
極板を移動させてからスイッチを開いたので、極板間の電位差はV₀となります。
- 図3における
極板Aの電気量をQ₃とおくと
Q₃=4CV₀・・・③
(これが正解です) - 静電エネルギーをU₃とおくと
U₃=Q₃V₀/2=2CV₀²・・・④
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(7)に関して、ここでシチュエーションが変わります。誘電体をΔxだけ移動させています。この状態における「静電エネルギーU₄」を答えます。
ポイントは
- 誘電体が入ってない部分C₃
- 誘電体が入っている部分C₄
で、2つのコンデンサーが並列になっているとみなす事です。
- C₃=2C・Δx/L
C₄=4C・(L-Δx)/Lより - 並列つなぎとみなした
コンデンサーの合成容量は
C₃+C₄
=2C{Δx+2(L-Δx)}/L
=2C(2L-Δx)/L - よって
U₄=Q₃²/2(C₃+C₃₄)
=4LCV₀²/(2L-Δx)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(8)に関して、図3→図4へ移る際の「静電エネルギーの増加量の式」が与えられており、この中で使われている「文字α」を答えます。
ポイントは「問題文で与えられた式」です。
「U₄/U₃」が「1/(1-α)」に相当するので、U₄/U₃を求めればよいと解ります。
- U₄/U₃
=2L/(2L-Δx)
=1/(1-Δx/2L)・・・(※) - よって
問題文で与えられた式と(※)を比較して
α=Δx/2L
(これが正解です)
合格者さんでも一定数が不正解になるレベルです。
よって、合否を分ける1問より少し難しい問題です。
(9)に関して、「外力がした仕事=静電エネルギーの増加量」という関係を使い、図4における「静電気力の大きさと向き」を答えます。
ポイントは、問題文「ΔU≒αU₃」をそのまま使うことです。
静電エネルギーの変化(ΔU)がそのまま「外力の仕事」になる、という条件が与えられています。そして「仕事=力×距離」なので、仕事から距離を割ってあげれば「外力の大きさ=求める静電気力の大きさ」が求まります。
- 題意より
ΔU≒αU₃
=CV₀²Δx/L - x軸正方向への外力をFとすると
静電気力に逆らって外力がした仕事は
FΔx=CV₀²Δx/L
∴ F=CV₀²/L(>0)
より外力は正方向となる - よって
誘電体にはたらく静電気力は
外力と逆方向なので
「負」方向となる
(これが正解です) - その大きさは
外力の大きさに等しく
CV₀²/L
(これが正解です)
本問自体は、合否を分ける1問レベルです。
しかし、本問へ参加するには(8)の正解が必要です。
よって、(8)とセットで、合否を分ける1問より少し難しい問題です。
(10)に関して、ここでシチュエーションが変わります。図4の状態から外力を0にした時の「誘電体の運動」を考えます。その運動を正しく描いたグラフを8択から答えます。
ポイントは「力学の運動方程式」です。
- 誘電体の質量をm
x軸方向の加速度aとして
運動方程式より
ma=-CV₀²/L
∴ a=-CV₀²/mL - よって
誘電体は等加速度運動をするため
誘電体の位置は
時間tの二次関数となる - そして、xが負の値になると
静電気力の向きは正方向となり
やはり誘電体の位置は
時間tの二次関数となる - 以上の条件を満たす
グラフは②である
(これが正解です)
合格者さんでも一定数が不正解になるレベルです。
よって、合否を分ける1問より難しい問題です。
大問3
問1に関して、語句問題です。問題で描かれている複スリットを使った実験は「ア:ヤング」の実験と呼ばれています。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(1)に関して、千春さんが求めた「sの平均を表す式」を答えます。
- 暗線の間隔の3倍を求めた
- 「暗線の間隔の3倍」の平均を計算した
- 以上の条件より
{(x₃-x₀)+(x₄-x₁)+(x₅-x₂)}/9
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、浩介さんが求めた「sの平均を表す式」を答えます。
- {(x₁-x₀)+(x₂-x₁)+(x₃-x₂)+(x₄-x₃)+(x₅-x₄)}/5
=(x₅-x₀)/5
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、(2)「浩介さんの計算」より(1)「千春さんの計算」の方が、計算精度が高くなる理由を答えます。
ポイントは「項の数」です。
千春さんの計算式はx₀~x₅まで項が6つあるのに対し、浩介さんの計算はx₀とx₅の2項しかありません。この理由を答えれば正解です。
- 千春さんの計算式ではx₀~x₅まで6つのデータを使えている事に対し、浩介さんの計算式ではx₀とx₅の2つのデータしか使えていないから。また、浩介さんの計算式が有効数字2桁である事に対し、千春さんの計算式は有効数字3桁で構成されているから。
(これが解答例です)
不合格者さんの一定数が不正解になるレベルです。
合否を分ける1問より少し簡単なレベルです。
問3に関して、問題文中の「エ」に入る記述を答えます。
ポイントは「(エ)直前の明線に関する記述を流用すること」です。
(エ)暗線の条件は、明線の条件から半波長ズレただけです。
- πずれているから
経路差ΔLが半波長の奇数倍に等しくなる
xd/L=λ(2m+1)/2(m=0,±1,±2,・・・)
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくる部分です。
よって、合否を分ける1問です。
問4に関して、表A・表Cの数値を使い、光源からの「光の波長λ」を答えます。
ポイントは「明線条件の式においてm=1を使うこと」です。
これにより「x=s」とできるため正解が求まります。
- 明線条件の式においてm=1の時
λ=xd/mL
=sd/L
=4.00×10⁻³×0.105×10⁻³/0.700
=6.00×10⁻⁷(m)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問5(1)に関して、ここでシチュエーションが変わります。最初の単スリットをX₀だけずらした時の「明線条件と暗線条件」を答えます。
ポイントは「丁寧に経路を再計算すること」です。
一見、問題文が長くて難しそうに見えますが、やっている事は「三平方の定理」です。
- P’BQ=√{L₀²+(d/2+X₀)²}+√{L²+(x+d/2)²}
- P’AQ=√{L₀²+(d/2-X₀)²}+√{L²+(x-d/2)²}
- ΔL’=P’BQ-P’AQ
≒X₀d/L₀+xd/L - よって、明線条件は
X₀d/L₀+xd/L=mλ(m=0,±1,±2,・・・)
(これが正解です) - また、暗線条件は
X₀d/L₀+xd/L=λ(2m+1)/2(m=0,±1,±2,・・・)
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問5(2)に関して、単スリット動かしたことによる「明線の移動方向」を答えます。
ポイントは「m=0について考えること」です。
m=0の明線はx=0の位置にあったので、移動後の位置が正の値なら正方向へ動いた、負の値なら負方向へ動いたと言えます。
- (1)の明線条件の式において
m=0とすると
X₀d/L₀+xd/L=0
∴ x=-X₀L/L₀ - よって
明線の移動方向は「向きb」
移動距離は「X₀L/L₀」
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
九州大学の物理2019年・平成31年度
大問1
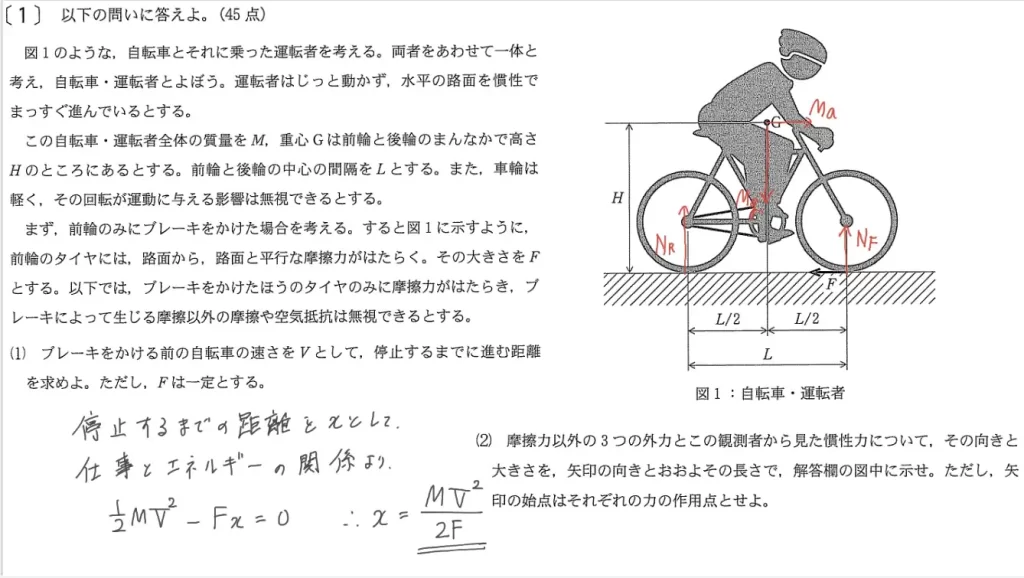
(1)に関して、ブレーキをかけた自転車が停止するまでに「進む距離」を答えます。
- 停止するまでの距離をxとおくと
仕事とエネルギーの関係より
1/2・MV²-Fx=0
∴ x=MV²/2F
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(2)に関して、作図問題です。摩擦力以外の3つの外力と観測者から見た慣性力を図中に描き込みます。
- 前輪の地面との接点から鉛直上向きにNF
- 後輪の地面との接点から鉛直上向きにNR
- 重心Gが鉛直下向きにMg
- 重心Gから水平右向きにMa
- (5)の結果より、NF>NR
上記5つを描き込むと正解です。
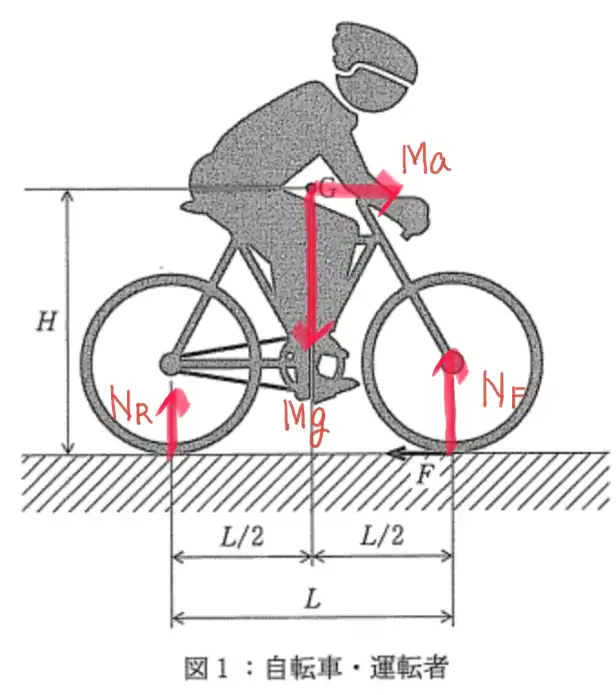
(5)の結果より「NF>NR」とする部分が少し難しいです。
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(3)に関して、前輪・後輪の垂直抗力による力のモーメントを答えます。
- 前輪:NF・L/2
- 後輪:-NR・L/2
以上が正解です。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(4)に関して、観測者から見た力のモーメントのつり合い条件の式を答えます。
- 水平方向:Ma-F=0
- 鉛直方向:Ma-NF-NR=0
- 重心Gまわり:NF・L/2-NR・L/2-FH=0
以上が正解です。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(5)に関して、(4)を解き「加速度の大きさ、垂直抗力の大きさ2つ」を「摩擦力Fの関数」として表します。
- (4)の3式より
a=F/M
NF=Mg/2+HF/L
NR=Mg/2-HF/L
以上が正解です。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(6)に関して、FとNFの比「F/NF」をFの関数としてグラフに描きます。
- (5)より
F/NF
=2LF/(MgL+2HF)
=2L/(MgL/F+2H)
上式に関して、Fを横軸に、F/NFを縦軸にグラフを描くと正解です。
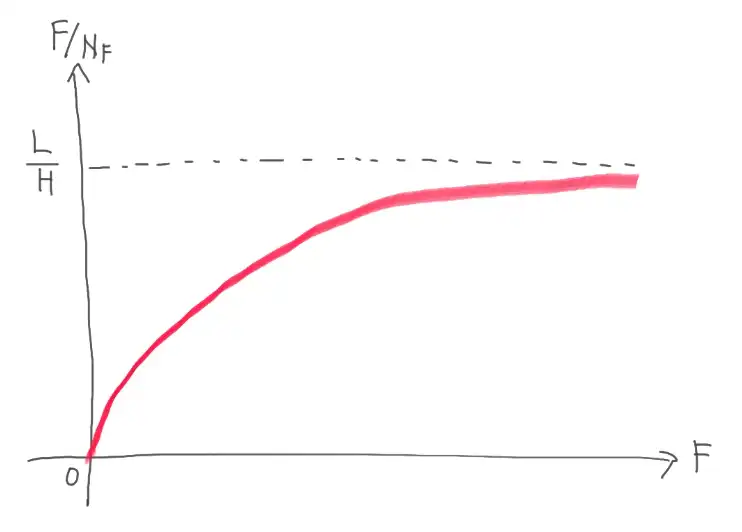
分母・分子をFで割る発想が、少し難しいです。
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(7)に関して、後輪が浮き上がらないために「Fが満たすべき条件」を答えます。
ポイントは「垂直抗力」です。
後輪が地面から浮き上がる瞬間「垂直抗力=0」となります。つまり、後輪が浮き上がらない条件は「NR≧0」となります。
- 後輪が浮き上がらない条件は
NR≧0 - (5)の結果より
Mg/2-HF/L≧0
∴ F≦MgL/2H
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(8)に関して、後輪が浮き上がらずに得られる最も大きな減速、すなわち「aの最大値」を答えます。
ポイントは「(7)の結果」です。
(7)で求めたのは「後輪が浮き上がらないFの限界値」でした。これを(4)の結果「Ma-F=0」に代入すると正解が求まります。
- F=MgL/2H
Ma=F
より
a=Lg/2H
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
(9)に関して、(8)で求めた「最大の減速」を得るために「μが満たすべき条件」を答えます。
ポイントは「前輪の垂直抗力=重力Mg」です。
(8)で求めた「最大の減速」の時「後輪の垂直抗力=0」となるため、鉛直方向の力のつり合いは「NF=Mg」となります。本問の「タイヤが滑らない条件」は「F≦μMg」なので、計算を進めると「μの条件」に行き着く、という仕組みです。
- aが(8)で求めた値の時
NR=0なので
鉛直方向の力の釣り合いは
NF=Mg - 今、タイヤが滑らない条件は
F≦μMg
∴ MgL/2H≦μMg
∴ μ≧L/2H
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
(10)に関して、後輪のみにブレーキをかけて得られる「最大の減速」を答えます。
- 後輪にかかる摩擦力をFとおくと
前輪が浮かない条件
NF≧0より
Mg/2+HF/L≧0
∴ F≧-MgL/2H…(※)
となる必要がある。 - 今、最大摩擦力をMaxFとすると
MaxF=μNR
∴ MaxF=μ(Mg/2-HMaxF/L)
∴ MaxF=μMgL/2(L+μH)
となる - またb=F/Mより
Maxb
=MaxF/M
=μgL/2(L+μH)
これは(※)を満たす
合格者さんでも難しいレベルです。
(11)に関して、前輪・後輪にブレーキをかけて「最大の減速」を得た時の「前輪にはたらく摩擦力FF」と「後輪に働く摩擦力FR」を答えます。
- 観測者から見た
水平・鉛直方向の力のつり合いより
NF+NR=Mg
FF+FR=Mb - また力のモーメントのつり合いより
LNF/2 – LNR/2 =H(FF+FR)
∴ NF-NR=2H(FF+FR)/L - よって上3式より
NF=Mg/2+H(FF+FR)/L
NR=Mg/2-H(FF+FR)/L - 今、NR≧0より
NR=Mg/2-H(FF+FR)/L≧0
∴ FF+FR≦MgL/2H
∴ Max(FF+FR)=MgL/2H - よって
NF-NR=2H(FF+FR)/L=Mg
NF+NR=Mg
∴ NF=Mg、NR=0 - よって
FR=0となるため
FF=MgL/2Hとなる
(これが正解です)
合格者さんでも難しいレベルです。
大問2

問1に関して、作図問題です。問題文で与えられたグラフの様に磁束密度Bが変化する時、コイルに発生する誘導起電力をグラフに描きます。
ポイントは「電磁誘導の式」です。
「V₁=-dΦ/dt=-LD・dB/dt」という関係になっています。よって「dB/dt」の部分は「与えられたグラフの傾き」となります。
(1)に関して
| 時間 | 与えられた グラフ傾き | 正解の値 |
|---|---|---|
| 0≦t≦1 | 1 | -LD |
| 1≦t≦2 | 0 | 0 |
| 2≦t≦3 | -2 | 2LD |
| 3≦t≦4 | 1 | -LD |
| 4≦t | 0 | 0 |
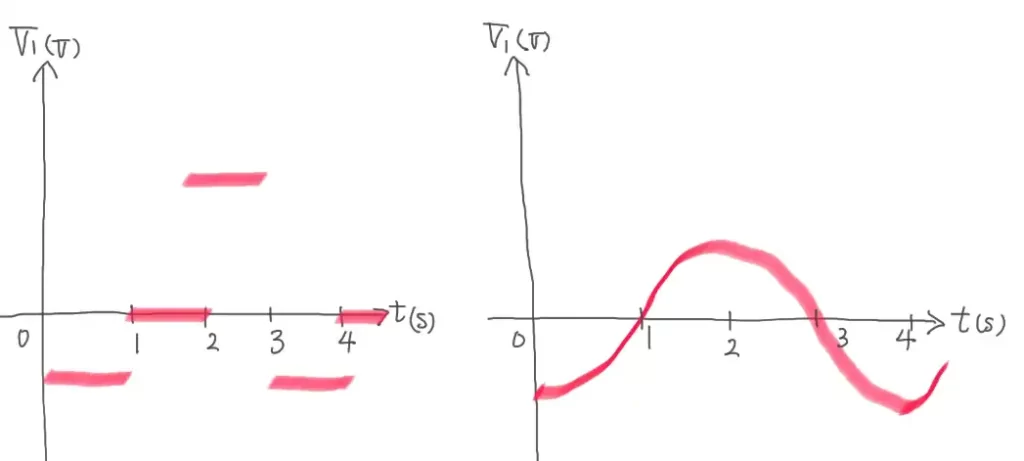
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2に関して、コイルを貫く磁場に関する「語句問題(ア)~(ク)」を答えます。
図のコイルは反時計回りに角度ωtだけ回転しているので、コイルを貫く磁束は時刻0の時に比べ減少しています。よって、電流の作る磁場がコイルを貫く磁束の時間変化を「ア:妨げる」向きに起電力が生じます。これを「イ:レンツの法則」といいます。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
今、コイルの回転によってコイルを貫く磁場が減っているので、それを増やす方向に電流が流れます。よって「ウ:(あ)」の方向です。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
この誘導電流は磁場の中を流れることになるため「エ:ローレンツ力」がコイルを流れる電流にはたらきます。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
電流をI、磁束密度の大きさをBと表すと、この力の大きさは「オ:BID」となります。コイルの「カ:cd」間にはたらく力も同じ大きさです。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
この力と同じ大きさ、反対向きの外力をかけるとコイルは一定の角速度で回転します。コイルab間については、力の仕事率は速度と力の内積なので、ab間の部分の速さをv(m/s)そこにかける力の大きさをF(N)とすると「仕事率=Fvsinωt」となります。cd間でも同じです。2つを合計した全体の仕事率P(W)は、FをIを用いて表すと「キ:P=2Fvsinωt=2BIDvsinωt」となります。
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
これと抵抗Rで単位時間あたりに発生する熱量PR(W)がエネルギー保存則により等しくなります。よって「P=PR」という関係が成り立ち、PRは電流Iを用いて「ク:PR=I²R」と表せるので、時刻tの時の電流はI=BLDωsinωt/Rとなります。
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問3に関して、問題文の図の様に
- 問2で使ったものと同じコイルを
- 問2のコイルと角度θだけずらして固定した
合体コイルを考えます。この合体コイルによる「仕事率P’」が時刻によらず一定になるような「θの値」を答えます。
ポイントは「問2までの流れを素直に問3へ移すこと」です。
問2の時点で
- P=I²R
- I=BLDω/R・sinωt
が判っていますから、これを「問2のコイル」と「問3で追加されたコイル」で素直に立式して解くだけです。
- 合体コイル全体の仕事率を
P’とおくと
P’=(BLDω/R・sinωt)²R+{BLDω/R・sin(ωt+θ)}²R - ところで
sin²ωt+sin²(ωt+θ)
=sin²ωt+(sinωtcosθ+cosωtsinθ)²
=(1+cos²θ)sin²ωt+(1-cos²θ)cos²ωt+2sinθcosθsinωtcosωt
=2cos²θsin²ωt+1/2・sin2θsin2ωt+1-cos²θ
である - よって
P’が時刻tによらず
常に一定の値をとる条件は
cos²θ=0 かつ sin2θ=0 - よって
θ=π/2
(これが正解です)
合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し難しい問題です。
続いて、P’がtの値によらず常に一定になることの「証明」に移ります。
- θ=π/2の時
P’=(BLDω/R・sinωt)²R+{BLDω/R・sin(ωt+π/2)}²R
=(BLDω)²/R・(sin²ωt+cos²ωt)
=(BLDω)²/R
=const
(証明終了)
同上です。
合否を分ける1問より少し難しい問題です。
大問3

問1に関して、状態方程式を使って「気体定数R」を表します。
ポイントは「状態方程式:PV=nRT」です
- 理想気体の状態方程式より
R=PV/nT
(これがaの正解です) - R=PV/nT
=2.7×10⁵×1.3×10⁻²/1.0×430
=8.2(J/mol・K)
(これがbの正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(1)に関して、図1の装置における「ピストンの質量」を答えます。
ポイントは「力のつり合い」です。
ピストンは静止しているので、鉛直方向の力のつり合いを書けば正解できます。
- ピストンにはたらく力のつりあいより
mg=pAS
∴ m=pAS/g
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、状態A→状態Bの間に「気体がする仕事WAB」を答えます。
ポイントは「定圧変化」です。
定圧変化なので「仕事=圧力×体積変化量」と求まります。
- 状態A→状態Bは定圧変化なので
WAB=pA(VB-VA)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、状態A→状態Bにおける「温度上昇」を答えます。
- 状態A・Bの気体温度をTA・TBとおくと
状態方程式より
pAVA=RTA
pAVB=RTB
- よって
求める温度変化をΔTABとして
ΔTAB
=TB-TA
=pA(VB-VA)/R
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(4)に関して、ヒーターから気体に与えられる熱QABを答えます。
ポイントは「熱力学第一法則」です。
気体が受け取った熱量=内部エネルギーの変化+外部にした仕事
- 熱力学第一法則より
QAB=ΔU+WAB
=3R/2・(TB-TA)+WAB
=3pA/2・(VB-VA)+pA(VB-VA)
=5pA/2・(VB-VA)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(5)に関して、状態Cにおける「気体の圧力」を答えます。
- 状態Cの圧力をpCとおくと
状態方程式より
pCVC=RTA
∴ pC=RTA/VC
=VApA/VC
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(6)に関して、状態B→状態Cの間に「気体がする仕事WBC」を答えます。
ポイントは「熱力学第一法則」です。
気体が受け取った熱量=内部エネルギーの変化+外部にした仕事
- 0=ΔU+WBC
=3R/2・(TA-TB)+WBC
∴ WBC=-3R/2・(TA-TB)
=3pA/2(VB-VA)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(7)に関して「WCAとQCAの間に成り立つ関係式」を答えます。
ポイントは「熱力学第一法則」です。
気体が受け取った熱量=内部エネルギーの変化+外部にした仕事
- -QCA=0+(-WCA)
∴ QCA=WCA
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(8)に関して、作図問題です。状態A→B→C→Aのサイクルに関して、pVグラフを作図します。
ポイントは以下の通りです。
| 状態 | 気体の変化 | グラフの概形 |
|---|---|---|
| A→B | p=pA 定圧変化 | 横一線 |
| B→C | pV^5/3=pAVB^5/3 断熱変化 | 下に凸な曲線 |
| C→A | pV=pAVA 等温変化 | 下に凸な曲線 |
上記をグラフに描いたものが正解となります。
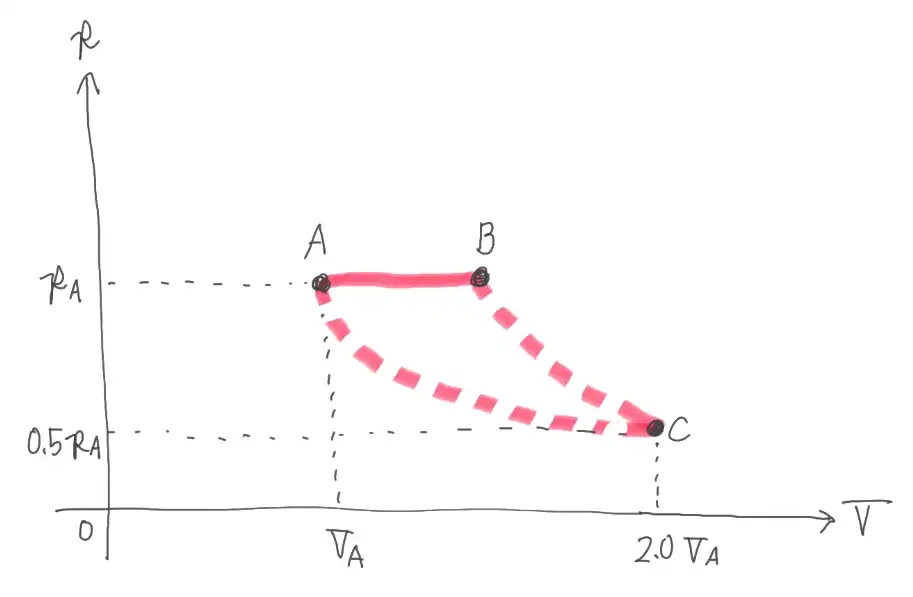
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(9)に関して、サイクルの熱効率に関して(ア)~(エ)に文字を入れます。
- このサイクルの熱効率eを
QAB、QCAを用いて表すと
e=(QAB-QCA)/QAB…(※)
(赤がア、青がイの正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
- 始点の状態Aから
終点の状態Aまでの
サイクル全体を通しての
気体の内部エネルギー変化は
「ウ:0」
であるので
「QAB-QCA」と同じ量を
WAB、WBC、WCAを用いて表すと
- QAB-WAB-WBC+WCA-QCA=0
∴ QAB-QCA=WAB+WBC-WCA
(これがエの正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
また、eの値は必ず1より「オ:小さい」
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
九州大学の物理2018年・平成30年度
大問1
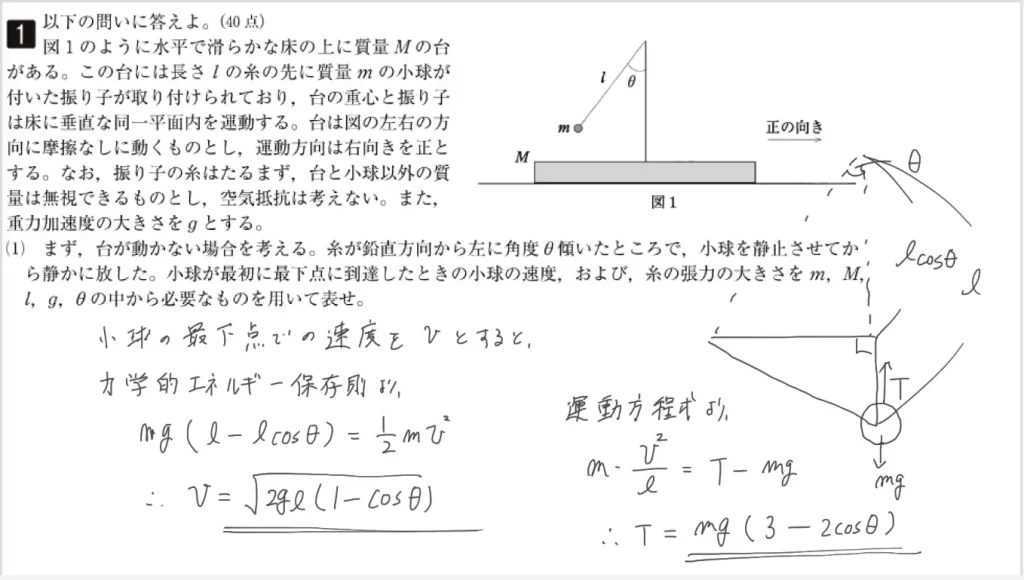
(1)に関して、台が固定された状態で小球を放した時の「小球が最初に最下点に到達した時の速度」および「糸の張力」を答えます。
ポイントは「力学的エネルギー保存則」です。
小球の初期位置から最下点まで、落下した分の位置エネルギーが運動エネルギーに変化します。
- 求める速度をvとおくと
力学的エネルギー保存則より
mg(l-lcosθ)=1/2・mv²
∴v=√{2gl(1-cosθ)}
(これが正解です) - 糸の張力をTとおくと
最下点における小球の
運動方程式より
m・v²/l=T-mg
∴ T=mg(3-2cosθ)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(2)に関して、台に静止した観測者から見た「小球の速度の最大値」を答えます。
ポイントは「台の加速中は、小球が静止すること」です。
つまり、先ほど解いた(1)と同じ要領で正解が出ます。
- 台の加速中に
小球が鉛直方向となす角を
θ₁とおくと
tanθ₁=ma/mg=a/g
∴ cosθ₁=g/√(g²+a²) - 求める小球の
最大速度を「vmax」とおくと
力学的エネルギー保存則より
mgl(1-cosθ₁)=1/2・mvmax² - ∴ MAX\(v=\sqrt{2gl\left( 1-\dfrac{g}{\sqrt{g^{2}+a^{2}}}\right) }\)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(3)に関して、(2)からシチュエーションが変わります。台を固定せず静止させ、小球を鉛直方向から60°の位置で放します。そして、小球が初めて最下点に到達した時の「小球の速度」と「台の速度」と「糸の張力」を答えます。
- 小球が最下点に達した時の
床に対する
小球と台の速度をv₆₀・V₆₀
糸の張力をT₆₀とおく - 運動量保存則と
力学的エネルギー保存則より
0=mv₆₀+MV₆₀
mgl(1-cos60°)=1/2・mv₆₀²+1/2・MV₆₀² - 小球の台に対する相対速度は
v₆₀-V₆₀なので
最下点での小球の
運動方程式は
m(v₆₀-V₆₀)²/l=T₆₀-mg
以上3式を解いて
- \(v_{60}=\sqrt{\dfrac{Mgl}{M+m}}\)
- \({V}_{60}=-m\sqrt{\dfrac{gl}{M\left( M+m\right) }}\)
- \(T_{60}=\dfrac{\left( 2M+m\right) mg}{M}\)
これらが正解です。
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
(4)に関して、(3)からシチュエーションが変わります。全てを静止させた状態から、台を撃力で右に初速度V₀で打ち出します。糸が水平になった時の「台の速度」を答えます。
ポイントは「糸が水平になった瞬間、小球と台の水平方向の速度が等しくなること」です。
この瞬間は、2つの物体の水平方向の速度を「1つの文字」で表すことができます。よって、式1本で正解が出ます。
- 糸が水平になった時の
台と小球の
水平方向の速度をWと置く - 水平方向の運動量保存則より
MV₀=(M+m)W
∴ \(W=\dfrac{MV_{0}}{M+m}\)
(これが正解です)
台と小球の速度が等しくなる事に気づく部分が少し難しいです。
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(5)に関して、糸が水平になった時の「小球の速度の大きさ」を答えます。
ポイントは「台と異なり、小球は鉛直方向の速度も持つ」ことです。
よって(4)の式は使えないため、力学的エネルギー保存則を使います。
- 求める小球の速度をwとおくと
力学的エネルギー保存則より
\(\dfrac{1}{2}MV_{0}^{2}=mgl+\dfrac{1}{2}mw^{2}+\dfrac{1}{2}Mw^{2}\)
∴ \(W=\sqrt{\dfrac{M\left( 2M+m\right) V_{0}^{2}}{\left( M+m\right) ^{2}}-2gl}\)
(これが正解です)
(4)との違いが少し難しいです。
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(6)に関して、糸が水平になる高さまで小球が上がるための「台に与える初速の最小値」を答えます。
ポイントは「三平方の定理」です。
(4)と同様、糸が水平になった瞬間は「台と小球の水平方向の速度」が等しくなります。三平方の定理を使い「小球の速度」から「水平方向の速度」を引けば「鉛直方向の速度」が残ります。これが0以上になれば、正解の条件となります。
- 三平方の定理より
小球の鉛直方向の速度成分は
√(w²-W²)
となる - これが0以上の時
題意を満たすので
w²-W²≧0
∴ \(V_{0}\geqq \sqrt{\dfrac{2\left( M+m\right) gℓ}{M}}\)
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
大問2

問1(1)に関して、磁束密度→Bのy成分|By|とz成分|Bz|を求めます。
ポイントは「問題文の定義にそのまま従うこと」です。
点(x,y,z)における磁場の磁束密度→Bのx成分は0であり、y成分およびz成分はそれぞれBy=-cy、Bz=cz(cは正の定数)と表される。
と書いてあるので、そのまま従ってください。
- 棒MN,LKのyz平面における座標は
MN(-l,z)
LK(l,z) - よって、問題文より
|By|=cl,|Bz|=cz
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(2)に関して、自由電子が受けるローレンツ力の大きさを答える問題です。
ポイントは「磁場のz方向の成分は無視できること」です。
ローレンツ力は「電荷の進行方向に垂直な磁場」の影響で生じる力なので、電荷の移動方向に等しいz成分の影響は受けません。
- F=|-ev₀By|
=ev₀cl
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(3)に関して、ローレンツ力によって移動した電子が作る「電位差V」を答えます。
ポイントは「力のつり合い」です。
ローレンツ力と電場から受ける力による「つり合いの式」を立てると、自然に正解が出ます。
- 電場をEとすると
力のつり合いの式より
-eE+F=0 - (2)の結果より
E=v₀cl - よって
求める電位差の大きさVは
V=E・2l
=2v₀cl²
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(4)に関して、導体ループで消費される「電力P」を答えます。
ポイントは「(3)までの流れに乗る」ことです。
(2)でローレンツ力、(3)で電位差、と少しずつ話が大きくなってきてますので、(4)は「回路1周分」と自然な流れに乗ってください。
- LM、NKでは誘導起電力は生じない
- (3)の結果より
MN、LKで誘導起電力Vが生じ
回路の起電力の合計は
2V
となる - ループ内に抵抗Rが2つあるので
オームの法則より電流Iは
I=2V/2R
=2v₀cl²/R - よって
P=2RI²
=8v₀²c²l⁴/R
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(5)に関して、ループの落下に伴う、単位時間あたりの「位置エネルギーの変化の大きさ」を答えます。
ポイントは「位置エネルギー」です。
(4)まで電磁気の問題を解いてきましたが、一旦、力学に切り替えてください。
- ループが受ける重力:mg
t秒間の落下距離:v₀Δt
より - 位置エネルギーの変化
ΔE=mgv₀Δt - よって
単位時間あたりの
位置エネルギー変化ΔUは
ΔU=ΔE/Δt
=mgv₀
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(6)に関して、(5)までのエネルギー変化を参考に「落下の速さv₀」を答えます。
ポイントは「落下による位置エネルギーの減少は、すべて回路のジュール熱で使われた」と気付くことです。
そのために問(1)~(5)までがありました。
- ΔU=Pとなるので
(4)(5)の結果より
v₀=mgR/(8c²l⁴)
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(1)に関して、ループがΔhだけ落下した際の「磁束の変化ΔΦ」を答えます。
ポイントは「変化量=変化後-変化前」です。
一気に変化量を求めようとせず、「変化前」「変化後」と1つずつ丁寧に考えれば上手くいきます。
- ループはz軸に垂直なので
磁束Φ=Bz×面積
で考えればよく
Φ=cz(2l)²
と書ける - 今、Δhだけ落下した時
磁束はΦ+ΔΦとなるので
Φ+ΔΦ=c(z-Δh)(2l)² - よって、上2式を引き算して
ΔΦ=-4cl²Δh
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(2)に関して、(1)の落下が時間Δtで起きる時、導体ループに流れる電流の大きさを求めます。
ポイントは「電磁誘導の法則」です。
単位時間あたりの磁束の変化(|ΔΦ/Δt|)が誘導起電力の大きさとなります。起電力が判ればオームの法則につないで、電流が求まります。
- ループ内に発生する
誘導起電力をF’とすると
電磁誘導の法則より
V’=|ΔΦ/Δt|
=4ct²Δh/Δt - よって
オームの法則より
I=V’/2R
=2cl²Δh/RΔt
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(3)に関して、導体ループ各辺が磁場から受ける力の向きを答えます。
ポイントは「問2(1)の計算結果」です。
「ΔΦ=-4cl²Δh」と負の値になっています。よって、ループが落下することにより、ループを貫く磁束は減っています。よって、誘導電流は「磁束を貫く方向=反時計回り」に発生しています。
- 問2(1)の結果より
電流Iは反時計回りに流れている - よって、左手の法則より
正解は(a)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(4)に関して、導体ループの運動方程式を答えます。
ポイントは「MN、LKが受ける上向きのローレンツ力」です。
- 磁場の「y方向成分」
- 反時計回りの「誘導電流」に
左手の法則を使ってみてください。上向きに力を受けることが解ります。
- 磁場のy方向成分|By|=clより
MN、LKは上向きに
I |By|・2l=2Icl²
の力を受ける - よって、求める運動方程式は
ma=4Icl²-mg
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
大問3

問1(1)に関して、文章中の(ア)~(オ)に入る式を答えます。
(ア)に関して
- 「道のり=速さ×時間」より
AO=ct₀
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(イ)に関して
- AB=速さ×1周期=v/f
AB’=ABcosθ=vcosθ/f
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(ウ)に関して
- BD=速さ×時間
=速さ×(t₀-1周期)
=c(t₀-1/f)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(エ)に関して
- DO=AO-AB’-B’D
≒AO-AB’-BD
=ct₀-vcosθ/f-c(t₀-1/f)
=(c-vcosθ)/f
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(オ)に関して
- 「速さ=振動数×波長」より
振動数=速さ/波長
=cf/(c-vcosθ)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(2)に関して、航空機の「点Oに対する角度」で変化する振動数をグラフに描きます。
- θ=0°:340/(340-170)×100=200Hz
- θ=90°:340/(340-0)×100=100Hz
- θ=180°:340/(340+170)×100≒67Hz
以上3つが正解です。

不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(1)に関して、シチュエーションが変わり「大気が2層」になります。大気の変わり目における「Φ₁とΦ₂の間に成り立つ等式」を答えます。
ポイントは「屈折の法則」です。
大気が二層になったので、境目で屈折の法則を使います。
- 屈折の法則より
sinΦ₁/sinΦ₂=c₁/c₂
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
(2)に関して、点Oに届いた音波の「波長と振動数」を答えます。
ポイントは「屈折後も振動数は変わらない」ことです。
- 大気Ⅰ・Ⅱの境目における
音波の振動数をf₁とおくと
f₁=c₁f/(c₁+vsinΦ₁) - Oにおける音波の振動数と
波長をf₂・λ₂とおくと
f₂=f₁=c₁f/(c₁+vsinΦ₁)
(これが正解です) - λ₂=c₂/f₂
=c₂(c₁+vsinΦ₁)/c₁f
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
(3)に関して、点Oに音波が届かなくなった時の「c₁の値」を答えます。
ポイントは「全反射」です。
点Oに音波が届かないという事は、大気の層で全反射したという事です。
- 点Oに音波が届かなかったということは
Φ₁=60°において
Φ₂=90°になったということである - よって
sin60°/sin90°=c₁/380
∴ c₁=√3/2 × 380
≒3.3×10²(m/s)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
九州大学の物理2017年・平成29年度
大問1
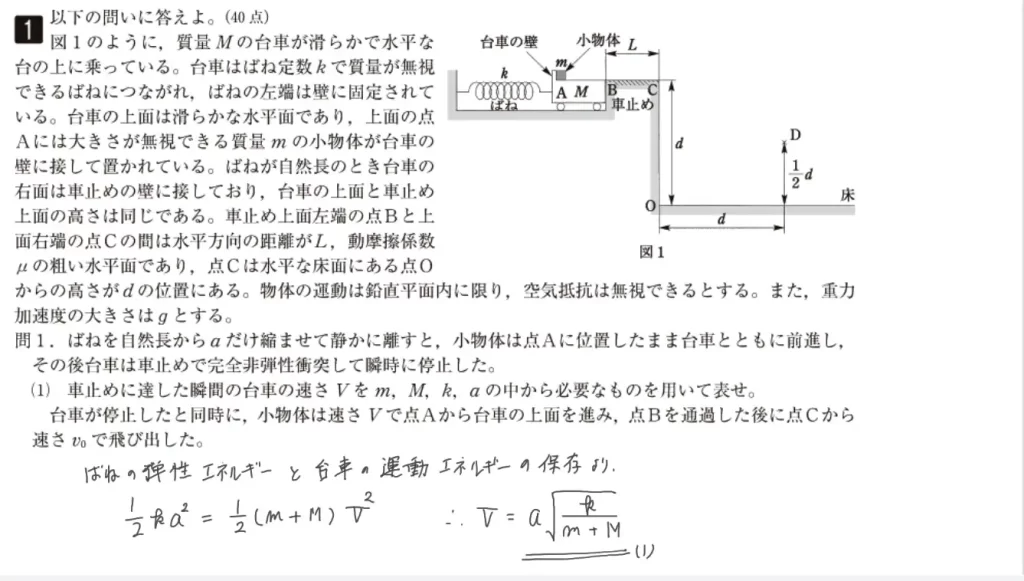
問1(1)に関して、車止めに達した瞬間の「台車の速さV」を答えます。
ポイントは「エネルギー保存則」です。
バネを縮めた際のエネルギーが、台車の運動エネルギーになっています。
- 1/2・ka²=1/2・(m+M)V²
∴ V=a√{k/(m+M)}
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、小物体が「点Cから飛び出す時の速さv₀」を答えます。
ポイントは「摩擦力の仕事」です。
速さVで台車から発射された小物体は、BC間で摩擦を受け速さv₀になります。
- 台車から発射された際の小物体の運動エネルギーは
BC間の摩擦力の仕事と
点Cにおける小物体の運動エネルギーになるので
1/2・mV²=μmgL+1/2・mv₀²
∴v₀=√{a²k/(M+m)-2μgL}…①
(これが正解です)
仕事とエネルギーなので、不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(3)に関して、点Cを速さv₀飛び出した小物体が「点Dを通過するようなv₀の条件」を答えます。
ポイントは「小物体が自由落下すること」です。
距離d/2だけ自由落下する時間は、計算で求まります。この時間で小物体が「右向きにd」進むような速さが、求めるv₀です。
- 小物体が点Cから点Dまでにかかる時間をtとすると
1/2・gt²=d/2
∴ t=√(d/g) - この時間で小物体は右向きにd進むので
v₀t=d
∴ v₀=d/t
=√(gd)…②
(これが正解です)
自由落下中の横方向の移動なので、不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(4)に関して、問3の様な状況(点Dを通る)となる「ばねの縮みa」を答えます。
ポイントは「(2)のv₀と(3)のv₀」です。
| (2)のv₀ | バネから放たれた小物体が点Cを飛び出す時の速さ |
| (3)のv₀ | 点Cを飛び出した小物体が点Dを通る条件 |
よって、(2)=(3)となれば、本問の条件を満たします。
- 題意を満たす条件は①=②なので
①②よりv₀を消去して
a=√{g(d+2μL)(M+m)/k}
(これが正解です)
少し難しくなりましたが、不合格者さんでも正解できるレベルです。
よって、全ての受験生さんが正解したい問題です。
問2(1)に関して、ここでシチュエーションが変わります。点Cで小物体が小球に衝突した直後の
- 小物体の速さv₁
- 小球の速さv₂
を答えます。
ポイントは「運動量保存則」です。
衝突した瞬間を考えれば「外力による力積」が加わらないため、運動量保存則を使えます。
- 衝突直前・直後の運動量保存則より
mv₀’=mv₁+mv₂…③ - また、はね返りの式より
v₁-v₂=-e(v₀’-0)…④ - ③④より
v₁=(1-e)v₀’/2(これが正解です)
v₂=(1+e)v₀’/2(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、小物体と小球の衝突で「失われた力学的エネルギーΔE」を答えます。
ポイントは「変化=後-前」です。
衝突前のエネルギーの方が大きい事は明らかなので
- |変化|=|後-前|=前-後
と、応用して使います。
- 衝突前の運動エネルギーは
1/2・mv₀’²…⑤ - 衝突後の運動エネルギーは
1/2・mv₁²+1/2・mv₂²…⑥ - ΔE=⑤-⑥
=(1-e²)mv₀’²/4
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(3)に関して、点Cを飛び出した小球が壁ではね返り、点Dで小物体と2度めの衝突をする時の「反発係数e」を答えます。
ポイントは「2物体の横方向の移動距離」です。
2物体が縦方向にd/2自由落下する時間で
- 小物体は横方向にd
- 小球は横方向に3d
移動します。小球と壁が弾性衝突するからです。
- 壁と弾性衝突した小球と小物体が
点Dで再び衝突するということは
一定時間の間に
小物体はd移動し
小球は3d移動したことを示す - よって
小球の速さは小物体の3倍なので
3v₁=v₂
∴e=1/2
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問2(4)に関して、小物体と小球が「床に落下する前に衝突」するための「ばねの縮みa’」を答えます。
ポイントは「2物体が自由落下する」ことです。
2物体が床に着くまでの時間t₁は計算で求まるので、この時間内に「2物体の移動が終わればよい」と解ります。
- 点Cを飛び出した2物体が
床に着くまでの時間をt₁とおくと
1/2・gt₁²=d
∴ t₁=√(2d/g)…⑦ - また、点Cを飛び出した小球が
壁に跳ね返って小物体と衝突する
までの時間をt₂とおくと
v₂t₂=3d…⑧ - 題意よりe=1/2なので
v₂=(1+e)v₀’/2
=3/4v₀’…⑨ - v₀’をa’を使って表すと
①より
v₀’=√{a’²k/(m+M)-2μgL}…(10) - t₂<t₁となれば
床に達する前に2物体が衝突するので
⑦⑧⑨を代入して
4d/v₀’<√(2d/g)
さらに(10)を代入して
a’>√{2(m+M)g/k・(4d+μL)}
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてきます。
よって、合否を分ける1問です。
大問2
問1(1)に関して、電子の周回によって「原点に発生する磁束密度B₀」を答えます。
- 磁場の強さをHとおくと
H=I₀/2r - よって
B₀=μ₀H
=μ₀I₀/2r(T)
(これが正解です)
「磁場の強さH」は間違えやすいポイントです。
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(2)に関して、磁束密度B₀の「向き」を答えます。
ポイントは「右ネジの法則」です。
【右ネジの法則】
電流の進行方向に対し「右ネジを回す向き」に磁界が発生する。
- マイナスの電荷を持った電子が
反時計回りに動いているため
電流の向きは時計回りである - よって、右ねじの法則より磁界は
「②Z軸負の向き」
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、電流定義に基づいて「I ₀」を答えます。
ポイントは「1秒」です。
問題文の「電流の定義に基づいて」とは「1秒間に流れる電気量を使え」という意味です。
- 電子の速さv₀より
電子は円周を1秒間に
v₀/2πr周する - また、電子1個の電気量はeなので
電流の定義に基づいて
I₀=ev₀/2πr(A)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問3に関して、電子の運動方程式を使い「速さv₀」を答えます。
ポイントは「クーロン力」です。
電子は円の中心にある原子核に引かれて円運動しているので、運動方程式の右辺にクーロン力を書きます。
- 電子の運動方程式より
mv₀²/r=k₀e²/r²
∴ v₀=√(k₀/mr)(m/s)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4(1)に関して、ここでシチュエーションが変わります。下から磁場Bがかかる時、電子が受ける「ローレンツ力の大きさf」を答えます。
- ローレンツ力→fの大きさは
f=evB(N)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問4(2)に関して、(1)の「力の向き」を答えます。
ポイントは「左手の法則」です。
- 左手の法則より、ローレンツ力の向きは
「④電子から原点に向かう向き」
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問5(1)に関して、以下の式に当てはまる(ア)(イ)を答えます。
- v²=(ア)×{1+(イ)×B×v}
ポイントは「与式の左辺v²」です。
これは「電子の速さの2乗」なので、電子の運動方程式を使えばよいと解ります。
- 電子の運動方程式より
mv²/r=k₀e²/r²+evB
∴ v²=k₀e²/mr・(1+r²Bv/k₀e)…①
(これがアとイの正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問5(2)に関して、磁場をかけたことによる「電子の速さの変化Δv₀」を答えます。
ポイントは「問5(1)の活用」です。
- 与式より
v²≒v₀²+2v₀×Δv₀
=k₀e²/mr+2v₀Δv₀(∵問3)…② - ①と近似式「B×v≒B×v₀」より
v²=k₀e²/mr・(1+r²Bv₀/k₀e)…③ - ②=③より
k₀e²/mr+2v₀Δv₀=k₀e²/mr・(1+r²Bv₀/k₀e)
(赤色部分を右辺へ移項して)
∴ 2v₀Δv₀=k₀e²/mr・r²Bv₀/k₀e
∴ 2v₀Δv₀=erBv₀/m
∴ Δv₀=er/2m×B
(これがウの正解です)
合格者さんでも一定数の不正解者が出るレベルです。
よって、合否を分ける1問より難しい問題です。
問6に関して、電子の速さの変化による「原点の磁束密度の変化ΔB₀」を答えます。
ポイントは「変化=後-前」です。
- B₀=μ₀/2r・I₀より
ΔB₀=μ₀/2r・ΔI₀
=μ₀/2r・(ev/2πr-ev₀/2πr)(∵問2)
=μ₀/2r・e/2πr・(v-v₀)
=μ₀/2r・e/2πr・Δv₀
=μ₀/2r・e/2πr・er/2m×B(∵問5)
=μ₀e²B/8πmr(T)
(これが正解です)
合格者さんでも一定数の不正解者が出るレベルです。
よって、正解できれば他者に差をつける1問です。
問7に関して、磁場をかけた事による電子の運動の変化から生じる「磁場の変化ΔB」を答えます。また、電子の円運動を逆向きにした時のΔBをΔB’とした時の「ΔB’の向き」を答えます。
ポイントは「ローレンツ力の向き」です。
問6までの電子の運動(反時計回り)の場合、左手の法則より、ローレンツ力の向きは「円の中心方向」でした。しかし、電子が逆向き(時計回り)に運動すると、ローレンツ力は「円の外側方向」に働きます。
- 電子が反時計回りの時の運動方程式は
問5(1)より
mv²/r=k₀e²/r²+evB
電子が時計回りの時の運動法方程式は
ローレンツ力が逆向きになるため
mv²/r=k₀e²/r²-evB - ゆえに、電子が反時計回りの時は
電子の速度が上がるため
時計回りの電流が増える - また、電子が時計回りの時は
電子の速度が下がるため
反時計回りの電流が減る - よって、電子が時計回りの時は
z軸負の向きの磁場が増え
電子が反時計回りの時は
z軸正の向きの磁場が減る - よって、ΔBおよびΔB’の向きは
「④両方ともz軸の負の向き」となる
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
大問3
問1(1)に関して、真空(屈折率1)から平面鏡(屈折率1より大)で光が反射する際の「位相のずれ」を答えます。
- 屈折率が小さい物質から
屈折率が大きい物質へ波が入る時
位相は「πずれる」
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、光子1個が平面鏡に与える力積の大きさを答えます。
ポイントは「運動量」です。
「力積の大きさ=運動量の変化の大きさ」なので、反射前後の光子の運動量を求めれば正解できます。
- 反射前の光子の運動量は
hν/c
反射後の運動量は
運動方向が逆になるため
-hν/c - よって、光子が平面鏡に与える
力積の大きさは
|力積|=|-hν/c-hν/c|
=2hν/c
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(1)に関して、ここでシチュエーションが変わります。
| l₁ | 「スリット→点P」の距離 |
| l₂ | 「スリット→平面鏡→点P」の距離 |
とした時の「l₂-l₁」を答えます。
ポイントは「三平方の定理」です。
| 区間 | 距離 |
|---|---|
| スリット~スクリーン | L |
| 平面鏡~スリット | d |
| 平面鏡~点P | x |
各区間の距離は上記のとおりなので、三平方の定理で求まります。
- l₁=√{L²+(x-d)²}
l₂=√{L²+(x+d)²} - よって
l₂-l₁
=√{L²+(x+d)²}-√{L²+(x-d)²}
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(2)に関して、(1)において近似を使った時の「鏡に最も近い明線の位置x」を答えます。
ポイントは「鏡に最も近い」という文言です。
つまり「1本目の明線」なので、光路差に対する波長のズレは「λ/2」となります。
- 与えられた近似を使い
問2(1)を書き直すと
l₂-l₁
=L[1+1/2{(x-d)/L}²]-L[1+1/2{(x-d)/L}²]
=2xd/L - 今、この光路差と半波長が等しくなるので
2xd/L=λ/2
∴ x=Lλ/4d
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問2(3)に関して、ここでシチュエーションが変わります。装置内を屈折率nの物質で満たし「鏡に最も近い明線の位置x」を答えます。
ポイントは「光路差」です。
屈折率1の真空から、屈折率nの物質に変わったため、光路差はn倍になっています。他は(2)と同じです。
- 光路差と半波長が等しくなるので
n(l₂-l₁)=λ/2
∴ n・2xd/L=λ/2
∴ x=Lλ/4nd
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問3(ア)に関して、ここでシチュエーションが変わります。真空中をx軸正の向きへ移動する平面鏡に対し、光子をぶつけた時の「エネルギー保存則の式」を答えます。
- 衝突前後で
鏡と光子のエネルギーの和は保存するので
1/2・MV²+hν=1/2・MV’²+hν’
∴ 1/2・MV’²-1/2・MV²=h(ν-ν’)
(これが正解です)
エネルギー保存の式を書くだけなので、不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3(イ)に関して、(ア)と同様で「運動量保存の式」を答えます。
- 衝突前後で
鏡と光子の運動量の和は保存するので
MV+hν/c=MV’-hν’/c
∴ MV’-MV=h/c・(ν+ν’)
(これが正解です)
エネルギー保存の式を書くだけなので、不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3(ウ)に関して、(ア)(イ)で求めた式を変形し「λ’/λ=」の形にします。
ポイントは「光の速さc」です。
「c=νλ」であり「c=ν’λ’」でもある事を、式変形で活用します。
- (ア)より
1/2・MV’²-1/2・MV²=h(ν-ν’)
∴ M/2・(V’+V)(V’-V)=h(ν-ν’)…① - (イ)より
MV’-MV=h/c・(ν+ν’)
∴ V’-V=h(ν+ν’)/Mc…② - 問題文より
V’+V≒2V…③ - ①に②③を代入して
M/2・2V・h(ν+ν’)/Mc=h(ν-ν’)
∴ ν/ν’=(c+V)/(c-V)…④ - ここで
c=νλ
c=ν’λ’
を④に代入して
λ’/λ=(c+V)/(c-V)
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問3(エ)に関して、ここでシチュエーションが変わります。光の速さcで時間t₀だけ進んだ時の距離「ct₀」を答えます。
ポイントは「問題文」です。
| 問題文 | 対応区間 | 長さ |
|---|---|---|
| 鏡は一定の速さVで動く | t=0とt=t₀ における 平面鏡の距離 | Vt₀ =AB’cosα |
| 線分ABの長さを入射波の波長λと等しくなるようにとる | AB | λ |
| t=0に点Aで反射した光は、t=t₀に点A’ | AA’ | ct₀ |
| 線分BB’の長さと線分AA’の長さは等しい | BB’ | ct₀ |
- 問題文より
ct₀
=AA’
=BB’
=BA+AB’
=λ+Vt₀/cosα
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問3(オ)に関して、反射波の波長λ’を答えます。
ポイントは「解答の形」です。
問題文に「λ’=ct₀+(オ)×cos(α+β)」と書いてありますが、これは問3(エ)までの情報より「λ’=AA’+AB’cos(α+β)」のことです。
- λ’=AA’+(オ)×cos(α+β)
=ct₀+AB’cos(α+β)
より
(オ)=AB’ - よって、問2(エ)より
(オ)=Vt₀/cosα
(これが正解です)
合格者さんでも一定数の不正解者が出るレベルです。
よって、合否を分ける1問より難しい問題です。
問3(カ)に関して、(エ)(オ)からt₀を消去した「λ’/λ」を答えます。
- (エ)の結果より
λ=ct₀-Vt₀/cosα - (オ)の結果より
λ’=ct₀+Vt₀cos(α+β)/cosα - よって
λ’/λ
={ccosα+Vcos(α+β)}/(ccosα-V)
(これが正解です)
合格者さんでも一定数の不正解が出るレベルです。
よって、合否を分ける1問より難しい問題です。
九州大学の物理2016年・平成28年度
大問1
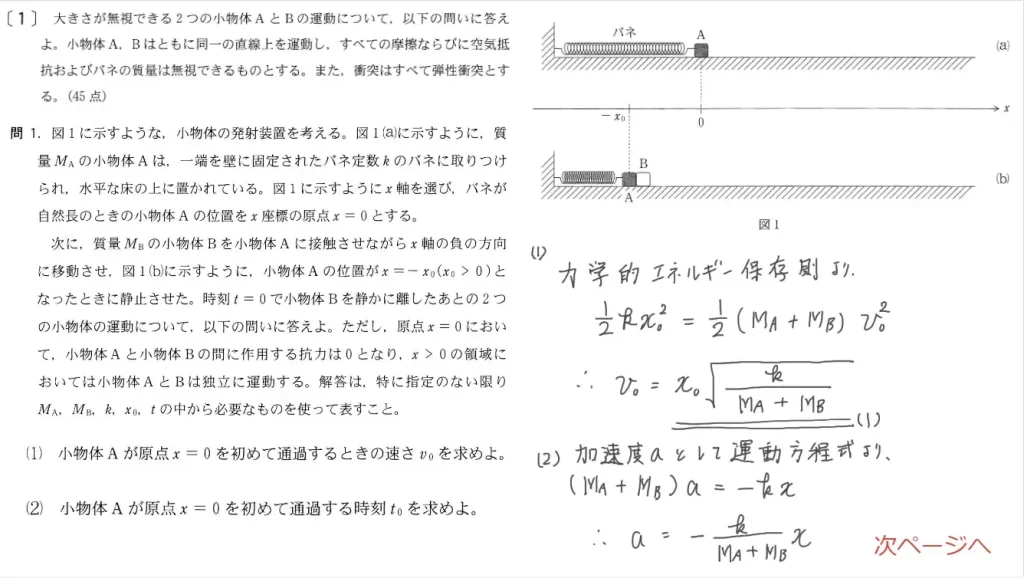
問1(1)に関して、小物体Aがx=0を「初めて通過する時の速さ」を答えます。
ポイントは「力学的エネルギー保存則」です。
摩擦力・空気抵抗を無視できるため、エネルギーは保存します。
- 力学的エネルギー保存則より
1/2・kx₀²=1/2・(MA+MB)v₀²
∴v₀=x₀√{k/(MA+MB)}…①
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、小物体Aがx=0を「初めて通過する時刻」を答えます。
ポイントは「運動方程式」です。
時間を求める問題なので、時間の関数(運動方程式)を使います。
- 小物体Aのx軸方向の加速度をaとして
運動方程式より
(MA+MB)a=-kx
∴ a=-kx/(MA+MB) - 上式より
小物体Aは単振動しており
角振動数ω:√{k/(MA+MB)}
周期T:2π√{(MA+MB)/k}
とわかる - よって
小物体Aが初めてx=0を通過するのは
t=T/4の時なので
t₀=T/4
=π/2・√{(MA+MB)/k}
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(3)に関して、時刻t₀以降の「小物体Aの位置xA(t)」を答えます。
ポイントは「三角関数」です。
小物体Aは単振動するので、三角関数を使って位置を表現できます。
- t=t₀以降
小物体Aは小物体Bと離れて運動する
この時のAの加速度をa₁とおくと
運動方程式より
MAa₁=-kx
∴ a₁=-kx/MA
となるので、Aは単振動する - この単振動は
振動中心:x=0
角振動数:ω₁=√(k/MA)…②
周期:T₁=2π√(MA/k)…③
であり
振幅をSとおくと
力学的エネルギー保存則より
1/2・MAv₀²=1/2・kS²
∴ S=v₀√(MA/k)…④
となる
単振動において「振幅、角振動数、Aの運動方向」の3点が判ったので、三角関数を使ってAの位置を表現できます。ここがポイントです。
- 小物体Aは時刻t₀において
x=0かつ速度が正方向なので
xA(t)=Ssinω₁(t-t₀)
(②④を代入します)
=v₀√(MA/k)・sin{√(k/MA)・(t-t₀)}
(①を代入します)
=x₀√{MA/(MA+MB)}・sin{√(k/MA)・(t-t₀)}
(これが正解です)
不合格者さんには難しく、合格者さんは正解してきます。
よって、合否を分ける1問です。
問1(4)に関して、時刻t₀以降の「小物体Bの位置xB(t)」を答えます。
ポイントは「等速直線運動」です。
- 時刻t₀以降
小物体Bは一定速度v₀で運動するので
xB(t)=v₀(t-t₀)
=x₀√{k/(MA+MB)}・(t-t₀)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(1)に関して、ここでシチュエーションが変わります。壁で跳ね返ったBが再びAと合体して運動できるような「壁の位置」および「Bが初めて壁に衝突する時刻」を答えます。
ポイントは「壁で反射したBがx=0に戻ってきた時の、Aの運動」です。
壁で反射したBとAが再び合体するためには、Aが左向きにx=0を通過していればよいと解ります。
- Bが壁に衝突する時刻をt₁とおくと
Aから離れたBが
x=0で再びAと一体になるまでの時間は
2(t₁-t₀)…⑤
となる - この時Aが単振動の1/2周期を終え
x=0を左向きに通過すれば
再びBと合体できるため
④⑤より
T₁/2=2(t₁-t₀)
∴ t₁=t₀+π/2・√(MA/k)
(これが正解です)
続いて「反射壁の位置」です。ここまで来ればすぐ出ます。
- よって、反射壁の位置D₀は
D₀=v₀(t₁-t₀)
=πx₀/2・√{MA/(MA+MB)}
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(2)に関して、小物体A・Bの位置に関して「1周期分のグラフ」を作図します。
問2(1)までの情報をまとめると、以下の図が正解となります。
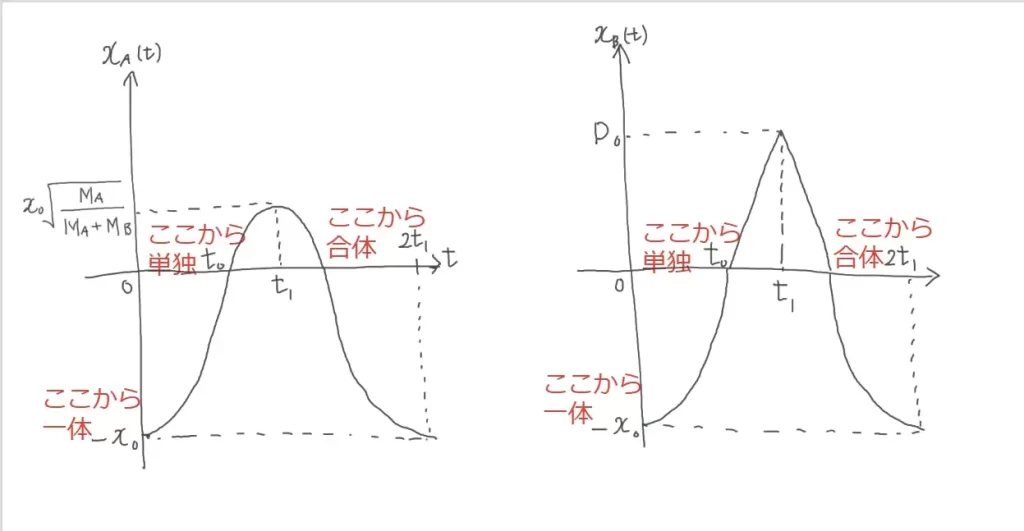
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(3)に関して、小物体A・Bが周期的に分離・合体を繰り返すための「壁の位置x=Dpが満たすべき条件」を答えます。
| pの値 | 分離→合体 までの時間 | Bの走った距離 | 壁の位置 |
|---|---|---|---|
| 0 | T₁/2 | v₀・T₁/2 | 1/2(v₀・T₁/2) |
| 1 | T₁/2+T₁ | v₀・3T₁/2 | 1/2(v₀・3T₁/2) |
| 2 | T₁/2+2T₁ | v₀・5T₁/2 | 1/2(v₀・5T₁/2) |
| 3 | T₁/2+3T₁ | v₀・7T₁/2 | 1/2(v₀・7T₁/2) |
上記より、Bの走った距離は「v₀・T₁(1/2+p)」と表現できます。この半分が「壁の位置」なので、以下の様に正解できます。
- Dp=1/2{v₀・T₁(1/2+p)}
(①③を代入します)
=1/2・x₀√{k/(MA+MB)}・2π√(MA/k)・(1/2+p)
=(p+1/2)πx₀√{MA/(MA+MB)}
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問3(1)に関して、ここでシチュエーションが変わります。
- A・B一体となった運動からBが放出される
- 壁で跳ね返ったBが、x=0でAと正面衝突する
- 再び壁で跳ね返ったBが、今度はAと合体する
- 1に戻る
上記が起きるための「壁の位置x=Lpが満たすべき条件」を答えます。
| 壁が最も近くにある場合 (p=0の時) | Aの移動距離 | Bが走った距離 |
|---|---|---|
| 一体となったA・BからBが放出された | 0 | 0 |
| 壁から戻って来たBがAと正面衝突 | 単振動1周期分 | v₀・T₁ |
| 再び壁から戻ってきたBがAと合体 | 単振動1周期分 | v₀・T₁ |
| 合計 | 単振動2周期分 | 2v₀・T₁ |
| 壁が少し離れた場合 (p=1の時) | Aの移動距離 | Bが走った距離 |
|---|---|---|
| 一体となったA・BからBが放出された | 0 | 0 |
| 壁から戻って来たBがAと正面衝突 | 単振動2周期分 | 2v₀・T₁ |
| 再び壁から戻ってきたBがAと合体 | 単振動2周期分 | 2v₀・T₁ |
| 合計 | 単振動4周期分 | 4v₀・T₁ |
| 壁がもうチョット離れた場合 (p=2の時) | Aの移動距離 | Bが走った距離 |
|---|---|---|
| 一体となったA・BからBが放出された | 0 | 0 |
| 壁から戻って来たBがAと正面衝突 | 単振動3周期分 | 3v₀・T₁ |
| 再び壁から戻ってきたBがAと合体 | 単振動3周期分 | 3v₀・T₁ |
| 合計 | 単振動6周期分 | 6v₀・T₁ |
上記より、この運動にかかる時間は「(p+1)×2T₁」と解ります。よって「v₀×Bの走った時間=2Lp×2往復」と立式すれば正解できると解ります。
- (p+1)2T₁・v₀=2Lp×2
(①③とMA=MB=Mを代入します)
∴ (p+1)・4π√(M/k)・x₀√{k/(M+M)}=2Lp×2
∴ Lp=(p+1)πx₀/√2
(これが正解です)
合格者さんでも一定数の不正解者が出るレベルです。
よって、正解できれば他者に差をつける1問です。
問3(2)に関して、反射壁がx=L₀にある時の「小物体Aの位置のグラフ」を作図します。
ここまでの情報を総合して作図すると、以下が正解です。
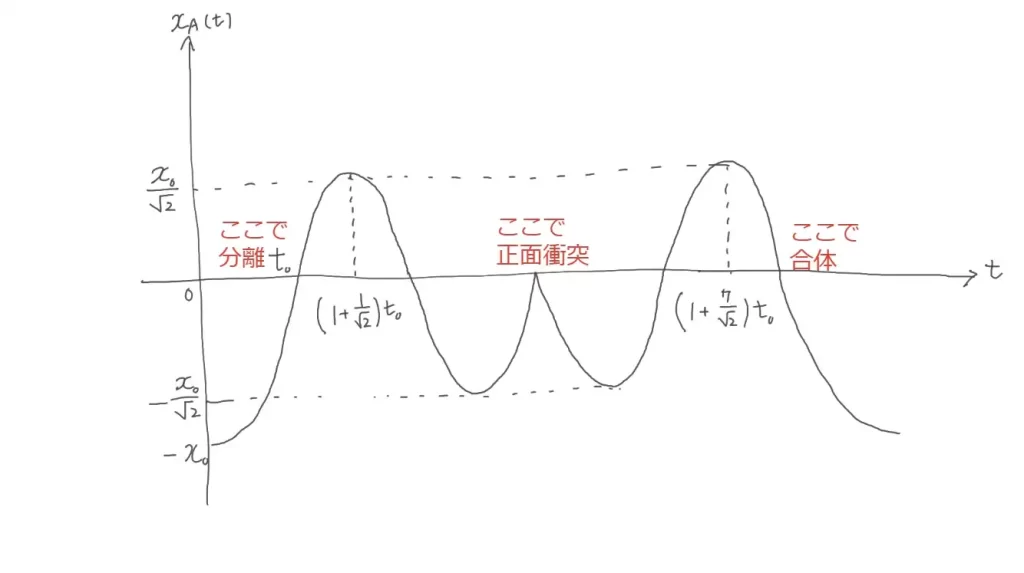
合格者さんでも一定数の不正解者が出るレベルです。
よって、正解できれば他者に差をつける1問です。
大問2
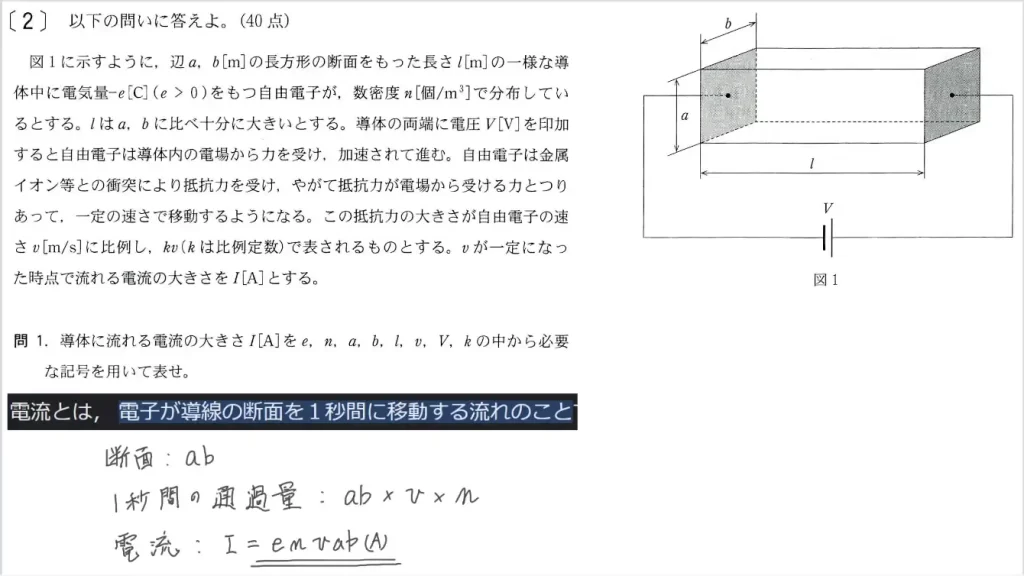
問1に関して、導体に流れる「電流の大きさ」を答えます。
電流は「単位時間あたりに導線の断面を通過する電気量」なので、以下の様に立式できます。
- I=envab(A)…①
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、自由電子が電場から受ける力と抵抗力が釣り合う時の「電子の速さ」を答えます。
ポイントは「力のつり合いの式」です。
問題文で「抵抗力=kv」が定義されているので、これを活用して立式します。
- 導体内の電場の強さをEとおくと
E=V/l - 力のつり合いの式より
eE=kv
∴ eV/l=kv
∴ v=eV/kl(m/s)…②
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、「抵抗Rと低効率ρ」を答えます。
ポイントは「問1と問2の式」です。
①式に②式を代入すると「IとVの式」ができるので、オームの法則に持ち込んで正解・・・という流れです。
- ①に②を代入すると
I=en・eV/kl・ab
∴ V=kl/e²nab・I
オームの法則より
R=kl/e²nab(Ω)
(これが正解です)
続いて「抵抗率ρ」です。
- R=ρ・l/abより
ρ=abR/l
=k/e²n(Ω・m)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問4(1)に関して、20.0℃における「導体の抵抗値」を答えます。
- 20.0℃における
抵抗率をρ₂₀
抵抗値をR₂₀
とおくと
R₂₀=ρ₂₀・l/ab
=1.00(Ω)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問4(2)に関して、温度20.0℃・電圧3.00Vにおける「電流の大きさ」と「1.00時間あたりのジュール熱」を答えます。
- オームの法則より
I=V/R₂₀
=3.00/1.00
=3.00(A)
(これが正解です)
続いてジュール熱です。
- 求めるジュール熱をWとすると
時間は3600(s)なので
W=3.00×3.00×3600
=3.24×10⁴(J)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問4(3)に関して、「100℃における抵抗値」を答えます。
ポイントは「20℃における抵抗値」です。
20℃の抵抗率は問題文で示されており、抵抗値は問4(1)で求めています。よって、20℃との比で考えれば正解できます。
- 100℃における抵抗値をR₁₀₀(Ω)とし
20℃における抵抗値と比較すると
1.00=ρ₀(1+4.30×10⁻³×20)×10.0/(4.00×10⁻⁴)²…③
R₁₀₀=ρ₀(1+4.30×10⁻³×100)×10.0/(4.00×10⁻⁴)²…④ - ④÷③より
R₁₀₀=1.43/1.086×1.00
≒1.32(Ω)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4(4)に関して、導体の温度を挙げると「抵抗値が増加する理由」を60字以内で答えます。
- 導体の温度が上がると陽イオンの熱運動が激しくなり、自由電子との衝突回数が増えることで電流が流れにくくなるから。(55字)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問5に関して、ここでシチュエーションが変わります。下から磁場をかけた事による「ローレンツ力の大きさと向き」を答えます。
ポイントは「左手の法則」です。
- まず、電子1個にはたらくローレンツ力の大きさは
fM=evB(N)
(これが正解です) - 向きは左手の法則より
x軸の正方向
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問6に関して、ローレンツ力によって移動した自由電子による「電場から電子1個が受ける力の大きさ」を答えます。
- 電子1個が電場から受ける力の大きさは
fE=eE(N)
(これが正解です) - 向きは
x軸の負方向
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問7に関して、問5のローレンツ力と問6の電場による力が釣り合う時に「成り立つ式」を答えます。
- 力のつり合いより
evB=eE
∴ E=vB
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問8に関して、試料中の「自由電子の数密度n」を答えます。
ポイントは「nが含まれた式」です。
本問の条件から立式しnを求める問題なので、1本は「nを含んだ式」が必要です。この視点から過去の問題を見ると
- 問1の「Iの式」
- 問3の「Rの式」
どちらかを使うだろうと解ります。
- 試料の2面間の電位差VHに関して
VH=Eb
=vBb(∵問7) - これを問1の①に代入すると
n=I/evab
=I/eab・Bb/VH
=IB/eaVH(個/m³)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
大問3
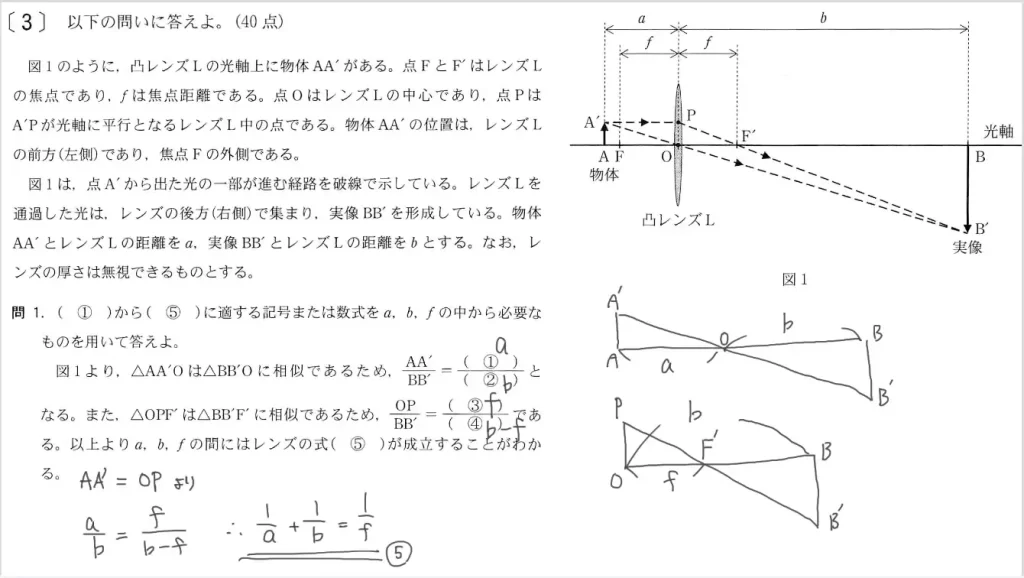
問1に関して、レンズに関する空所①~⑤に適切な記号・数式を入れます。
ポイントは「AA’=OP」です。
レンズ・物体・実像が作る直線によって「△AA’O∽△BB’O」と「△OPF’∽△BB’F’」という2つの相似関係が存在します。そして「AA’=OP」が明らかな事により、この2つの相似関係をつないで1つの式を導くことができます。
- △AA’O∽△BB’Oより
AA’/BB’=a/b
(これが①②の正解です) - また、△OPF’∽△BB’F’より
OP/BB’=f/(b-f)
(これが③④の正解です) - 以上とAA’=OPより
a/b=f/(b-f)
∴ 1/a+1/b=1/f
(これが⑤の正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、レンズを右向きに移動させて、スクリーンに再び鮮明な像が現れた時の「物体とレンズの距離」と「倍率」を答えます。
ポイントは「問1のレンズの式」です。
問題文で「f=16,a=20」が与えられており、b(物体とレンズの距離)を求める問題なので、問1の式を流用できます。
- 問1⑤の式にa=20,f=16を代入すると
1/20+1/b=1/16
∴ b=80(cm)
(これが正解です) - また、倍率は
20/80=1/4
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、作図問題です。
- 点A’→点Pへ向かう光
- 点A’→点Oへ向かう光
- 虚像CC’の位置と大きさ
上記3点を図中に記します。
ポイントは「光の経路2つ」です。
| 物体から水平に出た光 | レンズで屈折して焦点を通る |
| 物体からレンズの中心へ向かう光 | 真っすぐ進む |
そして、2つの光が交わる点に像ができます。
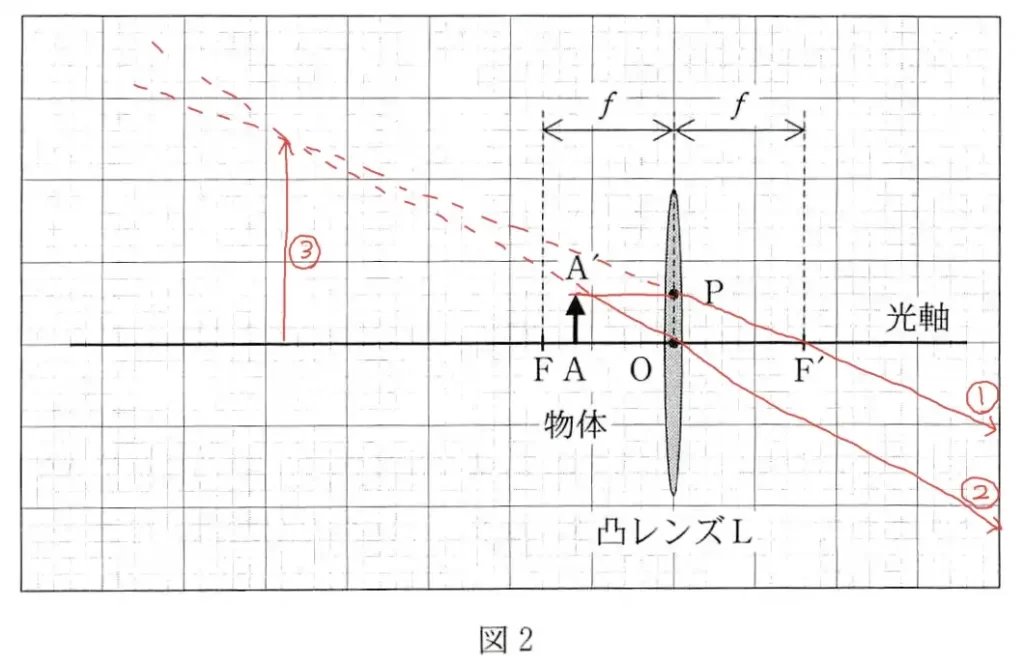
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問4に関して、f=16,AA’とLの距離を12とした時の「レンズと虚像の距離」を答えます。
ポイントは「問1のレンズの式」です。
像の位置が変わっていますが、レンズの式は使えます。
| 問題文 | レンズの式における |
|---|---|
| AA’とLの距離 | aのこと |
| レンズLと虚像CC’の距離 | bのこと |
よって、正解は以下の通りです。
- 問1⑤のレンズの式に
a=12,f=16を代入して
1/12+1/b=1/16
∴ b=-48(cm) - よって
レンズLと虚像CC’の距離は
48(cm)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問5に関して、ここでシチュエーションが変わります。「倍率DD’/AA’」を答えます。
ポイントは「問1と同じ解き方」です。
レンズが2枚に増えましたが、問5に関わるのはレンズL₁だけです。よって、問1と同じ解き方で正解できます。
- 問1と同様にして
△OPF’∽△BB’Fより
DD’/AA’=DD’/OP=g/f₁
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問6に関して、「倍率EE’/AA’」を答えます。
ポイントは「実像DD’を、レンズL₂にとっての物体とみなすこと」です。
複雑な装置を、以下の簡単な2つの関係とみなすことができます。
| 関係1 | 物体AA’ レンズL₁ 実像DD’ |
| 関係2 | 物体DD’ レンズL₂ 虚像EE’ |
- レンズL₂の中心をO₂
L₂から実像DD’までの距離をdとおくと
レンズの式より
1/d+1/(-h)=1/f₂
∴ d=f₂h/(f₂+h) - よって
△O₂DD’∽△O₂EE’より
レンズL₂の倍率は
EE’/DD’
=(f₂+h)/f₂ - よって求める値は
EE’/AA’
=DD’/AA’・EE’/DD’
=g(f₂+h)/f₁f₂
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくる問題です。
よって、合否を分ける1問です。
問7に関して、レンズL₁を焦点距離が短いレンズL₃に変えた時の「物体AA’の位置」と「レンズの倍率」について答えます。
ポイントは「虚像JJ’の位置がEE’と同じ」という事実です。
レンズL₂周りの関係(上記・関係2)が変化しておらず、その上で、虚像の位置まで変化しないという事は「実像DD’の位置も変化してない」ということです。
レンズを取り替えた(L₁→L₃)のに実像DD’の位置が変化しない、という事は「物体AA’を移動させて補正した」という事です。
レンズ1と3で焦点距離が「f₃<f₁」なので、レンズ3による実像は「本来、DD’の左側に来るはず」です。DD’の位置から全く動いてないという事は「物体AA’を右に移動させた」という事です(これが正解です)
続いて、像の大きさに関して。物体AA’を右側に動かして、レンズ1と同じ位置に実像DD’を作ったという事は、レンズ3による実像の方が大きい事を示しています。よって「EE’>JJ’」となるため「EE’/AA’>JJ’/AA’」となります(これが正解です)
よって、総合して②が正解です。
合格者さんでも一定数の不正解者が出るレベルです。
よって、正解できれば他者に差をつける1問です。
問8に関して、「倍率JJ’/AA’」を答えます。
- レンズ3と物体AA’の距離をa’とおくと
レンズの式より
1/a’+1/(f₁+g)=1/f₃
∴ a’=f₃(f₁+g)/(g+f₁-f₃) - 三角形の相似より
DD’/AA’=(f₁+g)/a’
JJ’/DD’=(f₂+h)/f₂ - よって
JJ’/AA’
=JJ’/DD’・DD’/AA’
=(f₂+h)/f₂・(f₁+g)・(g+f₁-f₃)/f₃(f₁+g)
=(g+f₁-f₃)(f₂+h)/f₂f₃
(これが正解です)
合格者さんでも一定数の不正解者が出るレベルです。
よって、正解できれば他者に差をつける1問です。
九州大学の物理2015年・平成27年度
大問1
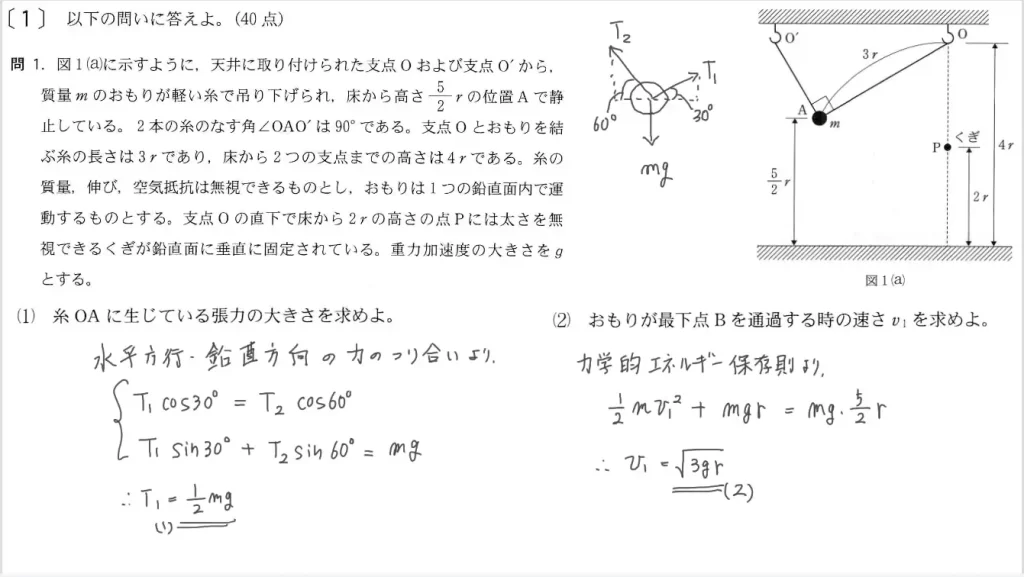
問1(1)に関して、糸OAの「張力の大きさ」を答えます。
ポイントは「力の分解」です。
おもりにかかる力を「水平方向」と「鉛直方向」に分解すると、張力が求まります。
- 糸OAによる張力をS₁
糸O’Aによる張力をS₂
とおく - 水平方向・鉛直方向の力のつり合いより
S₁cos30°=S₂cos60°
S₁sin30°+S₂sin60°=mg
∴ S₁=mg/2
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、おもりが点Bを通過する際の速さv₁を答えます。
ポイントは「力学的エネルギー保存則」です。
- 力学的エネルギー保存則より
1/2・mv₁²+mgr=mg・5/2r
∴ v₁=√(3gr)…①
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(3)に関して、おもりが点Bを通過する直前の張力T₁、直後の張力T₂の比「T₂/T₁」を答えます。
ポイントは「円運動の半径」です。
| 点Bを | 円運動の半径 |
|---|---|
| 通過前 | 3r |
| 通過後 | r |
- 点Bを通過前の
おもりの運動方程式より
m・v₁²/3r=T₁-mg…②
①②より
T₁=2mg…③ - 点Bを通過後の
おもりの運動方程式より
m・v₁²/r=T₂-mg…④
①④より
T₂=4mg…⑤ - ③⑤より
T₂/T₁=2
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(4)に関して、糸がたるまずに点C(円運動の頂上)に達するための「速さの最小値v₀」を答えます。
ポイントは「張力」です。
問題文の「糸がたるまずに」とは「張力が存在する」という事です。
- 点Cにおけるおもりの速さをv₂とおくと
力学的エネルギー保存則より
1/2・mv₀²+mg・5r/2=1/2・mv₂²+mg・3r
∴ v₂=√(v₀²-gr) - おもりが点Cにある時の
糸の張力をT₃とおくと
おもりの運動方程式より
m・v₂²/r=T₃+mg
∴ T₃=m・v₂²/r-mg
=m・v₀²/r-2mg - 点Cにおいて
糸がたるまない条件はT₃≧0より
m・v₀²/r-2mg≧0
∴ v₀≧√(2gr)
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくる問題です。
よって、合否を分ける1問です。
問1(5)に関して、点C→点Dにおける「水平方向の移動距離L」を答えます。
ポイントは「床に落下するまでの時間=水平に移動した時間」です。
- 条件より
v₀=√(2gr)
なので
v₂=√(v₀²-gr)
=√(gr)…⑥ - おもりの鉛直方向の加速度の大きさはgなので
床に落下するまでの時間をtとして
1/2・gt²=3r
∴ t=√(6r/g)…⑦ - よって、⑥⑦より
L=v₂t
=√6r
(これが正解です)
本問自体は不合格者さんでも正解してくるレベルです。
しかし、本問に参加するには問1(4)の正解が必要です。
よって、問1(4)とセットで、合否を分ける1問です。
問2(1)に関して、ここでシチュエーションが変わります。1回目の小球放出後の「台の速度V₁」を答えます。
ポイントは「運動量保存則」です。
| 1回目 | 放出前 | 放出後 |
|---|---|---|
| 台の質量 | M | M-m |
| 台の速度 | 0 | V₁ |
| 小球の速度 | V₁-v |
- 小球の放出前後における運動量保存則より
(M-m)V₁+m(V₁-v)=0
∴ V₁=mv/M
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、2回目の小球放出直後の「台の速度V₂」を答えます。
ポイントは「運動量保存則」です。
問2(1)と同じ要領で正解できます。
| 2回目 | 放出前 | 放出後 |
|---|---|---|
| 台の質量 | M-m | M-2m |
| 台の速度 | V₁ | V₂ |
| 小球の速度 | V₂-v |
- 2回目の放出前後における運動量保存則より
(M-2m)V₂+m(V₂-v)=(M-m)V₁
∴ V₂=m(2M-m)v/{M(M-m)}…⑧
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(3)に関して、p回目の小球放出による「台の速度変化Vp-Vp-1」を答えます。
ポイントは「運動量保存則」です。
問2(1)と同じ要領で正解できます。
| p回目 | 放出前 | 放出後 |
|---|---|---|
| 台の質量 | M-(p-1)m | M-pm |
| 台の速度 | Vp-1 | Vp |
| 小球の速度 | Vp-v |
- p回目の放出前後における運動量保存則より
(M-pm)Vp+m(Vp-v)={M-(p-1)m}Vp-1
∴ Vp-Vp-1=mv/{M-(p-1)m}
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくる問題です。
よって、合否を分ける1問です。
問2(4)に関して、ここでシチュエーションが変わります。2個の小球を同時放出した直後の「台の速度U」を答えます。
ポイントは「運動量保存則」です。
問2(1)と同じ要領で正解できます。
| 1回目 | 放出前 | 放出後 |
|---|---|---|
| 台の質量 | M | M-2m |
| 台の速度 | 0 | U |
| 小球の速度 | U-v |
- 1回目の放出前後における運動量保存則より
(M-2m)U+2m(U-v)=0
∴ U=2mv/M…⑨
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(5)に関して、問2(4)で求めた速度Uと問2(2)で求めた速度V₂の「大小関係」を答えます。
ポイントは「引き算」です。
大小関係を知りたいので「V₂-U」を計算します。
- ⑧-⑨より
V₂-U
=m(2M-m)v/{M(M-m)}-2mv/M
=mv/{M(M-m)}
>0 - よって
V₂ > U
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくる問題です。
よって、合否を分ける1問です。
大問2
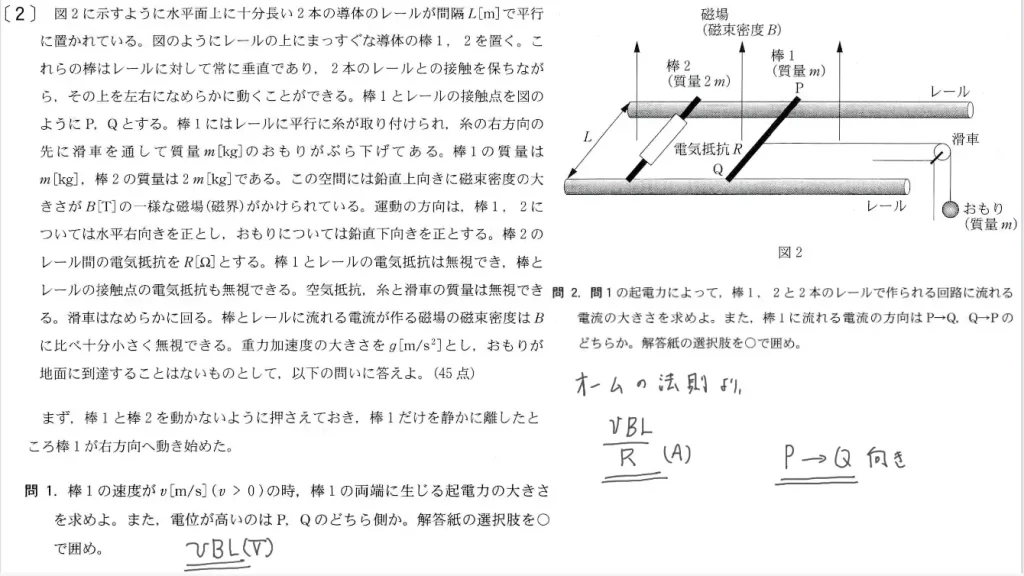
以下「単位」を省略して書きます。
回答の際は単位が必要です。
問1に関して、棒1に生じる「起電力の大きさ」を答えます。
| Δtにおける 回路の面積増加量 | vΔt・L |
| 回路を貫く 磁束の増加量 | ΔΦ =vΔt・L・B |
| 起電力 | V=ΔΦ/Δt =vBL (これが正解です) |
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、回路に流れる「電流の大きさ」を答えます。
ポイントは「オームの法則」です。
| 起電力 | vBL |
| 抵抗 | R |
| 電流 | I=V/R =vBL/R…① (これが正解です) |
続いて、電流の「向き」に関して。
- 条件より
回路を貫く磁束が増加しているため
誘導電流は
回路を貫く磁束を減らす方向に発生する - よって、電流は
「P→Q」の向き
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、棒1が磁場から受ける「力の大きさ」を答えます。
- 電流をIとすると
棒1が磁場から受ける力の大きさは
IBL=vB²L²/R(∵①)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問4に関して、棒1にかかる力がつり合った時の「棒1の速度の大きさ」を答えます。
ポイントは「力のつり合いの式」です。
糸が棒を引く力は、おもりにかかる重力mgに等しいです。これが棒にかかるローレンツ力とつり合います。
- 棒1に関する力のつり合いより
vB²L²/R=mg
∴ v=mgR/B²L²
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問5に関して、ここでシチュエーションが変わります。棒2の固定をはずし、動けるようにします。「棒2が動く向き」を答えます。
ポイントは「左手の法則」です。
棒2には電流が流れているため、磁場からローレンツ力を受け、その方向に移動します。
- 左手の法則より、棒2は
「右向き」に動き始める
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問6に関して、回路に流れる「電流の大きさ」を答えます。
ポイントは「棒2が動いていること」です。
棒2が動かない時の電流は、問2で求めました。よって、問1・問2を応用すれば正解できます。
| Δtにおける 回路の面積増加量 | (v₂-v₁)Δt・L |
| 回路を貫く 磁束の増加量 | ΔΦ =(v₂-v₁)Δt・L・B |
| 起電力 | V=ΔΦ/Δt =(v₂-v₁)BL |
| 電流 | I=V/R =(v₂-v₁)BL/R (これが正解です) |
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問7に関して、棒1・棒2の「運動方程式」を答えます。
- 左手の法則より
棒1が磁場から受けるローレンツ力の向きは
左向きである - よって、棒1の運動方程式は
ma₁=T-(v₁-v₂)B²L²/R…②
(これが正解です) - また、棒2の運動方程式は
2ma₂=(v₁-v₂)B²L²/R…③
(これが正解です)
本問自体は不合格者さんでも正解してくるレベルです。
しかし、本問に参加するには問6の正解が必要です。
よって、問6とセットで、合否を分ける1問です。
問8に関して、おもりの「運動方程式」を答えます。
- ma₁=mg-T…④
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問9に関して、「a₁」および「v₁-v₂」を答えます。
- 条件a₁=a₂
および②+③より
3ma₁=T…⑤ - ④⑤からTを消去して
4ma₁=mg
∴ a₁=g/4…⑥
(これが正解です) - また、③⑥より
v₁-v₂=mgR/(2B²L²)
(これが正解です)
本問自体は不合格者さんでも正解してくるレベルです。
しかし、本問に参加するには問6・問7の正解が必要です。
よって、問6・問7とセットで、合否を分ける1問です。
問10に関して、回路で発生する「単位時間あたりのジュール熱」を答えます。
ポイントは「ジュール熱の式」です。
【ジュール熱の式】
P=IV=IR²
- 問6の結果とジュール熱の式より
{(v₁-v₂)BL/R}²
=m²g²R/(4B²L²)
(これが正解です)
本問自体は不合格者さんでも正解してくるレベルです。
しかし、本問に参加するには問6の正解が必要です。
よって、問6とセットで、合否を分ける1問です。
※上記解説では「単位」を省略しています
大問3

問1に関して、第1室の「気体の物質量」を答えます。
ポイントは「状態方程式」です。
- 求める物質量をn₁とおくと
pAVA=n₁RTA
∴ n₁=PAVA/(RTA)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、状態A→状態Bの変化に際し、ヒーターが第1室の気体に「加えた熱量」を答えます。
ポイントは「熱力学第一法則」です。
- 受け取った熱量=内部エネルギー変化+外部への仕事
- 変化=後-前
上記2つを使います。
- 求める熱量をQとして
Q=3/2・n₁R(2TA-TA)+0
=3/2・pAVA
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、状態Cにおける「第1室・第2室の温度」を答えます。
ポイントは「全体で考えること」です。
断熱カバーを外したことで、第1室・第2室の状態は変化していますが、全体で見ると
- 外部から熱の出入りは無く
- 外部への仕事もしてない
ので、内部エネルギーは保存されます。よって、第2室の物質量を調べ、内部エネルギーの保存に持ち込めば正解・・・という流れです。
- 第2室の気体の物質量をn₂とおくと
pA・3VA=n₂RTA
∴ n₂=3pAVA/RTA
=3n₁ - 状態B→Cの前後で
内部エネルギーの総量は保存されるため
3/2・(n₁+n₂)RTC=3/2・n₁R・2TA+3/2・n₂RTA
∴ TC=5/4・TA
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4に関して、状態B→状態Cの際に、第1室から第2室へ「移動した熱量」を答えます。
ポイントは「第2室の内部エネルギーの増加量」です。
体積一定なので気体は外部に仕事をせず、受け取った熱量はそのまま「内部エネルギーの増加」になります。
- 第2室の内部エネルギーの変化をΔU₂として
ΔU₂=3/2・n₂R(TC-TA)
=3/2・n₂R(5/4・TA-TA)
=9/8・pAVA
(これが正解です)
不合格者さんでも正解してくるレベルです。
しかし、本問に参加するには問3の正解が必要です。
よって、問3とセットで、合否を分ける1問より少し簡単な問題です。
問5に関して、状態Cにおける「第1室・第2室の圧力」を答えます。
ポイントは「状態方程式」です。
「PV=nRT」において、第1室・第2室ともに以下の関係があります。
| n | 変化ナシ |
| R | 定数 |
よって、状態B→Cの前後で「PV/T=一定」より正解・・・という流れです。
- 第1室の圧力をpCとおくと
pAVA/TA=pCVA/(5/4・TA)
∴ pC=5/4・pA
(これが正解です) - 第2室の圧力をpC’とおくと
pA・3VA/TA=pC’・3VA/(5/4・TA)
∴ pC’=5/4・pA
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問6に関して、ここでシチュエーションが変わります。状態A→Dにおける第1室・第2室の「内部エネルギーの変化の和」を答えます。
ポイントは「全体で考えること」です。
第1室が温められ、隔壁が動いても、気体全体では外部に仕事をしません。よって、気体が受け取った熱量はそのまま「内部エネルギーの変化の和」となります。
- 気体全体で考えると
外部に仕事をしないので
ΔU₁+ΔU₂=3pAVA…①
(これが正解です)
「全体で考えればよい」と気付く部分がやや難しいですが、合否を分ける1問というほどではありません。
よって、合否を分ける1問より少し簡単な問題です。
問7に関して、状態A→Dにおける「第1室の内部エネルギーの変化量」を答えます。
ポイントは「状態Dにおける温度TDを求めること」です。
問6では「気体全体」を扱いましたが、問7では個別に考える出題となりました。よって、最終的に「内部エネルギー変化=3/2・n₁R(TD-TA)」を計算する必要があるため「TDが必要」となります。
- 第1室の気体の物質量が変化しないため
pV/T=一定
より
pAVA/TA=pDVD/TD
∴ TD=pDVD/pAVA・TA - よって
ΔU₁=3/2・n₁R(TD-TA)
=3/2・(pDVD-pAVA)…②
(これが正解です)
ボイル・シャルルの法則からTDを求める部分がやや難しいです。
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問8に関して、状態Dにおける「圧力pD」を答えます。
ポイントは「第2室の内部エネルギー変化」です。
| 内部エネルギー変化 | |
|---|---|
| 全体 | 問6の正解 |
| 第1室 | 問7の正解 |
| 第2室 | 未出 |
という流れなので「第2室の内部エネルギー変化」を求め
- 第1室+第2室=全体
という式を立てれば「圧力pD」が求まって正解・・・という流れになるはずです。
- 状態Dにおける第2室の
気体の体積をVD’、温度をTD’とおく - 第2室の気体の物質量は変化しないため
pV/T=一定
より
pA・3VA/TA=pD(4VA-VD)/TD’
∴ TD’=pD(4VA-VD)TA/3pAVA - よって
ΔU₂=3/2・n₂R(TD’-TA)
=3/2・(4pDVA-pDVD-3pAVA)…③ - ②+③=①より
pD=3/2・pA
(これが正解です)
「問8の問題文」がヒントにならないため、正解への道筋が見えにくいです。
よって、合格者さんでも一定数が不正解になるレベルです。
正解できれば他者に差をつける1問です。
九州大学の物理2014年・平成26年度
大問1
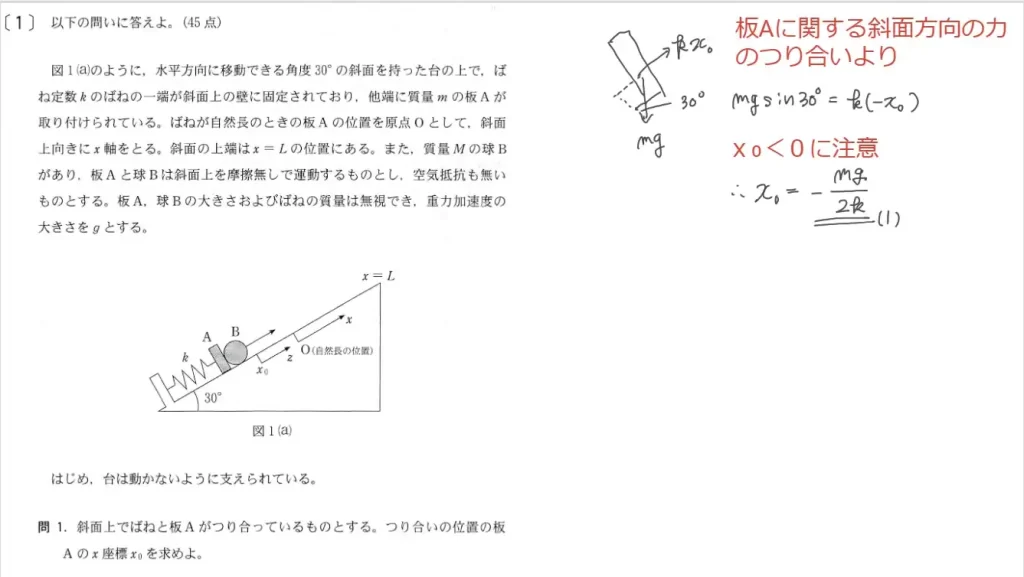
問1に関して、斜面上でバネと板Aがつり合っている時の「つり合いの位置」を答えます。
ポイントは「x₀が負の値」であることです。
問1で運動方程式の符号が逆になると、問2以降が全滅になるので注意が必要です。
- 板Aに関する斜面方向の
力のつり合いより
mgsin30°=k(-x₀)
∴ x₀=-mg/2k
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、板A・球Bの「運動方程式」を答えます。また「加速度a」および「球と板が押し合う力F」を答えます。
- 板Aに関する運動方程式より
ma=-kx-F-1/2・mg…①
(これが正解です) - 球Bに関する運動方程式より
Ma=F-1/2・Mg…②
(これが正解です) - ①+②より
a=-kx/(m+M)-1/2g…③
(これが正解です) - ③を②に代入して
F=-Mkx/(m+M)…④
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3(1)に関して、板A・球Bが「離れる瞬間のx座標」および「x方向の速度v」を答えます。
ポイントは「F=0」です。
Fは「板Aと球Bが押し合う力」ですが、これが0になると押し合いが無くなり、離れます。
- A・Bが離れる時
F=0
なので④よりx座標は
x=0
(これが正解です) - また、力学的エネルギー保存則より
1/2・kd²=(m+M)g・d/2+1/2・(m+M)v²
∴ v=√{kd²/(m+M)-gd}
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3(2)に関して、球Bの「最高到達点のx座標」を答えます。
ポイントは「最高点における速度=0」です。
よって「速度=0」となる時のBのx座標を求めれば正解・・・という流れです。
- Bのx軸方向の加速度をβとおくと
運動方程式より
Mβ=-1/2・Mg
∴ β=-g/2 - 最高到達点のx座標をhとおくと
0-v²=2βh
∴ h=kd²/(m+M)g-d
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問4(1)に関して、球Bと離れた後の「板Aの運動方程式」を答えます。
- 板Aの加速度をaAとおくと
maA=-kx-1/2・mg
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問4(2)に関して、問4(1)の式を「座標zの式」に書き直します。
- 問4(1)の式より
maA=-k(x+mg/2k)…⑤
∴ aA=-k/m・(x+mg/2k) - よって、この運動は
振動中心:-mg/2k
角振動数:√(k/m)…⑥
の単振動である - x=-mg/2kの時z=0なので
z=x+mg/2k
となり、これを⑤に代入して
maA=-kz
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4(3)に関して、板Aの「単振動の周期」を答えます。
- ⑥より
T=2π√(m/k)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問5(1)(2)に関して、ここでシチュエーションが変わります。動く台上から見た時の板A・球Bの「運動方程式」を答えます。
ポイントは「慣性力」です。
この運動方程式は「台上の観測者」の視点で立てるため、台の移動による慣性力を考えます。
- 板Aのx軸方向の運動方程式より
ma’=-kx-mgsin30°-F’+mαcos30°
∴ ma’=-kx-F’
(これが正解です) - 球Bのx軸方向の運動方程式より
Ma’=F’-Mgsin30°+Mαcos30°
∴ Ma’=F’…⑦
(これが正解です) - A・Bを一体とみなすと
(m+M)a’=-kx…⑧
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問5(3)に関して、台上の観測者から見た時の「x座標」と「速度v’」を答えます。
- ⑧より
a’=-kx/(m+M)…⑨ - よって、この運動は
振動中心:x=0
振幅:d
角振動数:√{k/(m+M)}
の単振動である - よって、座標は
x=dsin√{k/(m+M)}・t
(これが正解です) - 速度は
v’=d√{k/(m+M)}cos√{k/(m+M)}・t…(10)
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問6に関して、板A・球Bが離れる瞬間の「x座標」および台上の観測者から見た時の「x方向の速度」を答えます。
- ⑦⑨より
F’=-kMx/(m+M) - よって
F’=0となるのは
x=0の時
(これが正解です) - この時t=0なので(10)に代入して
v’=d√{k/(m+M)}…(11)
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問7に関して、台から飛び出した「球Bの最高点の高さ」を答えます。
- 球Bの斜面方向の加速度をβ’とすると
運動方程式より
Mβ’=-Mgsin30°+Mαcos30°=0
∴ β’=0
なので、球Bは(11)より速度
d√{k/(m+M)}
で、台を飛び出す - その球Bは重力による自由落下となるため
台を飛び出してから最高点までの高さh’として
0-{d√{k/(m+M)}・sin30°}²=-2gh’
∴ h’=d²k/{8(m+M)g} - よって、求める高さは
Lsin30°+h’
=L/2+d²k/{8(m+M)g}
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
大問2

問1(ア)に関して、スイッチを閉じた直後に流れる「電流」を答えます。
ポイントは「スイッチを閉じた直後」です。
この時コンデンサーは導線とみなせます。
- オームの法則より
E=rIcm
∴ Icm=E/r
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(イ)に関して、コンデンサーに電流Icが流れている時の「コンデンサーに蓄えられる電気量」を答えます。
- E=rIc+QA/C₁
∴ QA=C₁(E-rIc)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、作図問題です。コンデンサーAに流れる電流Icの時間変化をグラフに描きます。
- 0≦t<t₁において
Ic=0 - t₁<tにおいて
E=rIc+Vc
∴ Ic=(E-Vc)/r - これらを作図した以下が正解となる
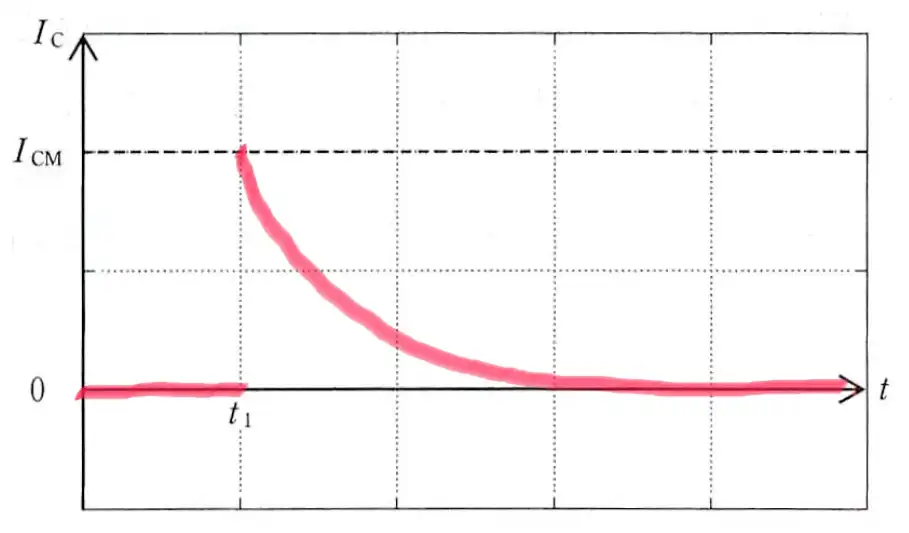
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問3に関して、コンデンサーAの極板間電圧が上がるのに「要する時間の長さ」を
- 内部抵抗が高い場合
- 内部抵抗が低い場合
の2者で比較します。また、その理由を「150字以内」で答えます。
ポイントは「電流の強さ」です。
内部抵抗が高ければ、回路に流れる電流が弱くなり、コンデンサーAの充電速度は低下します。よって、コンデンサーAの極板間電圧の上昇も遅くなります。
| 正解 | a:内部抵抗が高い方が時間を要する |
| 理由 | 内部抵抗が高い場合、コンデンサーAを流れる電流が小さくなるため、単位時間あたりコンデンサーAに蓄えられる電気量は小さくなる。コンデンサーAの極板間電圧は、コンデンサーAに蓄えられた電気量に比例するため、単位時間あたりに蓄えられる電気量が減れば、極板間電圧の上昇に時間を要するようになるから。(145字) |
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問4(ウ)に関して、スイッチ1を開き、コンデンサーAの極板間に誘電体を挿入した時の「静電容量の倍率」を答えます。
- 誘電体を挿入後の
静電容量をC₁’とおくと
C₁’/C₁=εr(倍)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4(エ)に関して、スイッチ1を開き、コンデンサーAの極板間に誘電体を挿入した時の「極板間電圧の倍率」を答えます。
ポイントは「電気量の保存」です。
スイッチ1を開いた事により、コンデンサーAに充電された電気量は変化しません。その上でコンデンサーには「Q=CV」という関係があるので・・・という流れです。
- スイッチ1を開いたことで
コンデンサーAの電気量Q₁は保存するので
Q₁=C₁E
Q₁=C₁’Vc’ - よって、上2式より
Vc’/E=1/εr(倍)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4(オ)に関して、スイッチ1を開き、コンデンサーAの極板間に誘電体を挿入した時の「静電エネルギーの倍率」を答えます。
ポイントは「電気量の保存」です。
問4(エ)と同じ仕組みで正解できます。
- スイッチ1を開いたことで
コンデンサーAの電気量は保存するので
挿入前後の静電エネルギーをU₁・U₁’として
U₁=Q₁²/2C₁
U₁’=Q₁²/2C₁’ - よって、上2式より
U₁’/U₁=C₁/C₁’=1/εr(倍)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問5(カ)~(ケ)に関して、問4の状態からスイッチ2を閉じた時の
- コンデンサーA・Bの極板間電圧
- コンデンサーA・Bの電気量
を答えます。
ポイントは「Aの電位差=Bの電位差」です。
2つのコンデンサーは導線でつながっているため、極板間電圧が等しくなります。
- コンデンサーA・Bに蓄えられる電気量を
Q₁’・Q₂’とおくと
スイッチ1を開けたことで電気量は保存するので
Q₁=Q₁’+Q₂’…① - コンデンサーA・Bの電位差は等しいので
Q₁’=C₁V’…②
Q₂’=C₂V’…③
①~③で「未知数3つ、式3本」なので、連立させれば正解が出ると解ります。
- ①~③より
V’=C₁E/(εrC₁+C₂)
(これが正解です)
Q₁’=εrC₁²E/(εrC₁+C₂)
(これが正解です)
Q₂’=C₁C₂E/(εrC₁+C₂)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問6に関して、問5の後でスイッチ3を閉じた事による「コイルに流れる電流の波形」を答えます。
ポイントは「正の電荷の動き」です。
- コンデンサーの左側に充電された「正の電荷」がコイルを通って右側へ移動する
- コンデンサーの右側が「正の電荷」で充電される
- コンデンサーの右側に充電された「正の電荷」がコイルを通って左側へ移動する
- 1へ戻る
よって正解は(d)となります。
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問7(コ)に関して、問6における電流波形の「周波数」を答えます。
電気振動の周期
| コンデンサの電圧 | Q/C |
| コイルの電圧 | L・dI/dt |
- 今、コンデンサとコイルは導線で結ばれており
電位が等しいので
L・dI/dt=Q/C…(A) - ところで、I=-dQ/dtなので
これを(A)に代入すると
-L・d²Q/dt²=Q/C
∴ d²Q/dt₂=-1/LC・Q…(B) - 今(B)において
Q→xと書き換えると
d²x/dt²=-1/LC・x - これは「力学」における
角振動数:ω=√(1/LC)
周期:T=2π/ω=2π√(LC)
の単振動である - よって
この電気振動の振動周期も
T=2π/ω=2π√(LC)
である
- 電気振動の周期は
T=2π√(LC)
よって、周波数は
f=1/T=1/{2π√(LC)}…④ - コンデンサーA・Bの合成容量は
C=εrC₁+C₂…⑤ - よって、④に⑤を代入して
f=1/{2π√L(εrC₁+C₂)}
(これが正解です)
合格者さんでも一定数が不正解になるレベルです。
よって、正解できれば他者に差をつける1問です。
問7(サ)に関して、問6における電流波形の「最大値」を答えます。
ポイントは「エネルギー保存則」です。
| エネルギーが全て | 式 |
|---|---|
| コンデンサーにある時 | 1/2・CV’² |
| コイルにある時 | 1/2・LI² |
この2式は「=」でつなげるため正解・・・という流れです。
- 電流の最大値をIとおくと
エネルギー保存則より
1/2・CV’²=1/2・LI²
∴ I=V’√(C/L)
=C₁E/√L(εrC₁+C₂)
(これが正解です)
合格者さんでも一定数が不正解になるレベルです。
よって、正解できれば他者に差をつける1問です。
問8に関して、コイルに抵抗を直列に接続した時の「電流振動の波形」を答えます。
ポイントは「ジュール熱」です。
問7まで(コイルとコンデンサーだけの時)は、回路におけるエネルギー消費が0でしたが、抵抗ではジュール熱として消費されます。よって、振動は減衰していくと解ります。
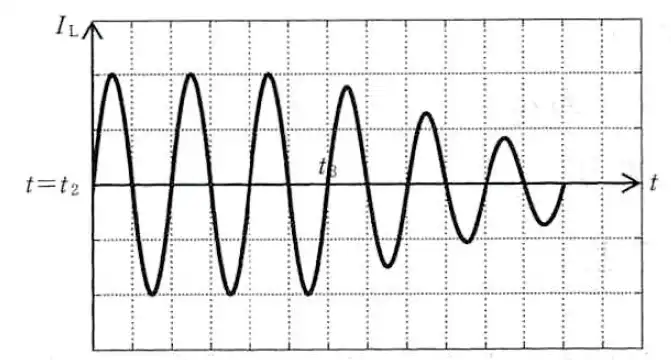
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
大問3

問1に関して、状態Aの「温度TA」を答えます。
- 状態O・状態Aに関する状態方程式より
状態O:p₀V₀=RT₀
状態A:p₀・2V₀=R・TA
∴ TA=2T₀
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、状態O→状態Aの間に「気体がした仕事WOA」と「気体が得た熱量QOA」を答えます。
ポイントは「定圧変化」です。
定圧変化の場合は「気体の仕事=定圧×体積変化」で求まるので活用します。
- 定圧変化なので
WOA=p₀(2V₀-V₀)
=RT₀
(これが正解です)
続いて「気体が得た熱量QOA」は「熱力学第一法則」を使います。
- 熱力学第一法則より
QOA=ΔU+WOA
=3/2・R(TA-T₀)+RT₀
=5/2・RT₀
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、状態Bにおける「温度TB」を答えます。
ポイントは「定積変化」です。
- 状態O・状態Bに関する状態方程式より
状態O:p₀V₀=RT₀
状態B:0.5p₀・V₀=RTB
∴ TB=0.5T₀
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問4に関して、状態O→状態Bにおける「内部エネルギーの変化ΔUOB」を答えます。
ポイントは「変化=後-前」です。
- ΔUOB=ΔUB-ΔUO
=3/2・R(TB-T₀)
=-0.75RT₀
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問5に関して、状態Cの「圧力pC」を答えます。
ポイントは「断熱変化」です。
断熱変化なので、ポアソンの式(pV⁵/³=一定)を使えます。
- ポアソンの式より
p₀V₀⁵/³=pC(2V₀)⁵/³
∴ pC=0.315p₀…①
≒0.32p₀
(これが正解です)
問5の直前の問題文に「pV⁵/³=一定の関係が成立する」と書いてあります。
よって、不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問6に関して、状態Cの「温度TC」を答えます。
ポイントは「温度・圧力・体積どれも一定ではない」ことです。
- 状態O・状態Cに関する状態方程式より
状態O:p₀V₀=RT₀
状態C:pC・2V₀=RTC
①より:pC=0.315p₀ - よって、上3式より
TC=0.63T₀…②
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問7に関して、状態O→状態Cにおける「内部エネルギー変化ΔOC」および「気体がした仕事WOC」を答えます。
ポイントは「断熱変化」です。
熱の出入りが無いため、熱力学第一法則の式(Q=ΔU+W)の左辺は0となります。
- ΔUOC=3/2・R(TC-T₀)
=-0.555RT₀(∵②)
≒-0.56RT₀
(これが正解です) - また、熱力学第一法則より
0=ΔUOC+WOC
∴ WOC≒0.56RT₀
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問8に関して、作図問題です。T-Vグラフにおいて
- 状態O→A
- 状態O→B
- 状態O→C
3つの変化を作図します。
ポイントは「比例関係」です。
点Oから3点A・B・Cにかけて、どの様な直線(または曲線)になるかは「P・V・Tの比例関係で決まります。
| 比例関係 | グラフの形 | |
|---|---|---|
| 状態O→A | 定圧変化なので T∝V | 直線 |
| 状態O→B | 定積変化なので V=一定 (T∝p) | 直線 |
| 状態O→C | ポアソンの式より pV⁵/³=一定 よって p=RT/Vより TV²/³=一定ゆえ T∝V⁻²/³ | 下向き凸 |
よって、正解は以下の通りです。
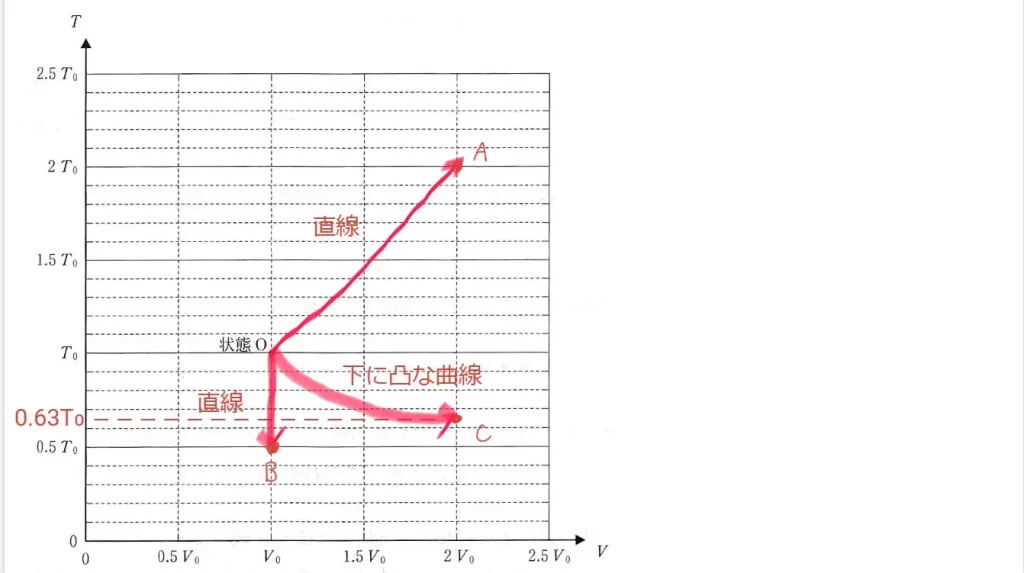
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問9に関して、状態O→A→C→Oのサイクルにおいて「状態A→Cで気体が得た熱量QAC」を答えます。
ポイントは「定積変化」です。
状態A→Cは定積変化なので、気体は外部に仕事をしていません。よって、熱力学第一法則より「受け取った熱量=内部エネルギー変化」となります。
- 状態A→Cは定積変化なので
気体は外部に仕事をしない - 熱力学第一法則より
QAC=ΔU+0
=3/2・R(TC-TA)
=3/2・R(0.63T₀–2T₀)
=-2.055RT₀
≒-2.06RT₀
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問10に関して、問9のサイクルの「熱効率e」を答えます。
ポイントは「熱効率の式」です。
【熱効率の式】
| サイクルに投入した熱 | Q₁ |
| サイクルから回収した熱 | Q₂ |
| サイクルで失った熱 | Q₁-Q₂ |
熱効率:e=(Q₁-Q₂)÷Q₁
- サイクルにおいて
吸収した熱:Q₁
放出した熱:Q₂
とおくと
Q₁:状態O→A
Q₂:状態A→C
より
Q₁=2.5RT₀
Q₂=2.055RT₀
となる - よって、熱効率eは
e=(Q₁-Q₂)÷Q₁
=1-Q₂/Q₁
≒0.18
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
九州大学の物理2013年・平成25年度
大問1
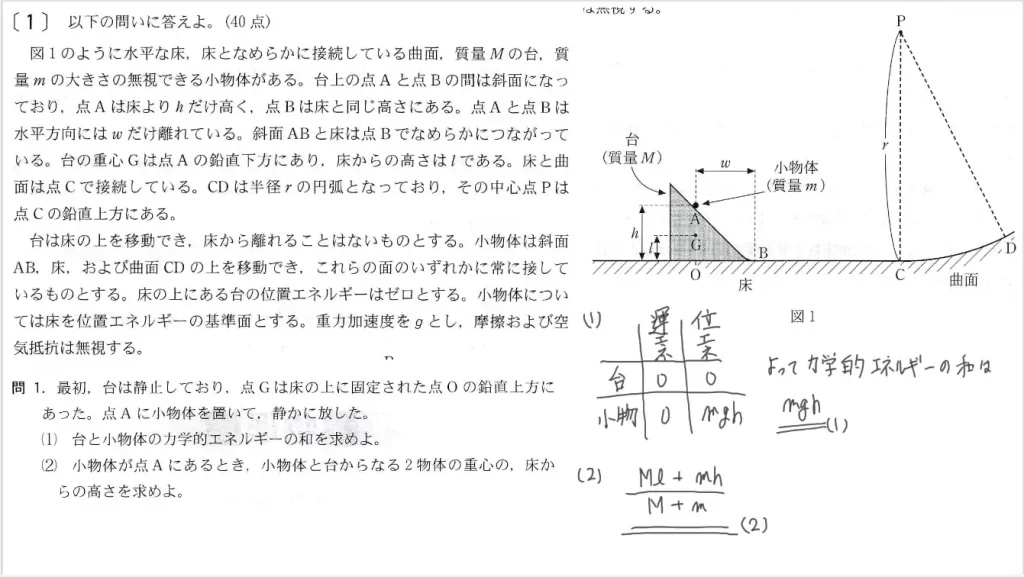
問1(1)に関して、台と小物体の力学的エネルギーの和を答えます。
ポイントは「力学的エネルギー=運動エネルギー+位置エネルギー」です。
| 運動エネルギー | 位置エネルギー | |
|---|---|---|
| 台 | 0 | 0 |
| 小物体 | 0 | mgh |
- 上記より
力学的エネルギーの和は
mgh
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、小物体が点Aにある時の「台と小物体からなる重心」を答えます。
ポイントは「重心の式」です。
重心の式
- 重心xg周りのモーメントのつり合いより
m₁(xg-x₁)=m₂(x₂-xg)
∴ 重心:xg=(m₁x₁+m₂x₂)/(m₁+m₂)
- 重心の式より
(Ml+mh)/(M+m)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2に関して、小物体が台上の点Bに来た時の「点Oから小物体までの距離」を答えます。
ポイントは、問題文「2物体の重心は水平方向には移動しない」です。
重心が移動しない、との事なので「水平方向の重心=0」の式を立てればよいと解ります。
- 点Oを原点と考える
初期状態における重心の水平方向の座標は
xG=0
となる - 小物体が点Bまで来た時の
点Oから小物体までの距離をx
点Oから台の重心までの水平方向距離をX
とおくと - X+x=w
xG={M(-X)+mx}/(M+m) - 上2式より
x=Mw/(M+m)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問3(1)に関して、語句問題です。
- 小物体と台は水平方向には
「ア:外力」
を受けないため、小物体と台の
「イ:運動量」
の水平成分の和は変化しません。
(これが正解です)
不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問3(2)に関して、台を離れた直後の小物体が「台の何倍の速さになるか」を答えます。
ポイントは「運動量保存則」です。
先程の問3(1)を立式します。
- 小物体が台から離れた直後の
小物体の速さv
台の速さV
とおくと、運動量保存則より
M(-V)+mv=0 - よって
v/V=M/m(倍)…①
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3(3)に関して、台を離れた直後の「小物体の速さ」を答えます。
ポイントは「力学的エネルギー保存則」です。
- 1/2・MV²+1/2・mv²=mgh…②
- ①②よりVを消去して
v=√{2ghM/(M+m)}…③
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4(1)に関して、点Dの「床からの高さ」を答えます。
ポイントは「力学的エネルギー保存則」です。
床面に摩擦が無く、坂を登っているので、力学的エネルギー保存を使います。
- 求める高さをHとおくと
力学的エネルギー保存則より
1/2・mv²=mgH…④ - ③④より
H=Mh/(M+m)…⑤
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4(2)に関して、「m/M=0」という条件の下に「点Dの床からの高さ」を答えます。
ポイントは「問4(1)の正解」です。
求める値は、問4(1)の正解で「m/M=0」としたものです。
- ⑤の分母・分子をMで割ると
H=h/(1+m/M)
=h/(1+0)
=h
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4(3)に関して
- 点Cから小物体までの円弧の長さx
- 小物体が受ける重力の曲面方向の成分F
とした時の「Fとxの間の比例定数」を答えます。
- 半径と中心角、および円弧の関係より
θ=x/r…⑥ - また
F=-mgsinθ
≒-mgθ…⑦(∵ θが十分小さい) - ⑥⑦より
F=-mgx/r
なので、比例定数は
-mg/r
(これが正解です)
「近似」と「円弧と中心角の関係」が重なっているため、不合格者さんには難しいです。
合格者さんは乗り越えてくるレベルなので、合否を分ける1問です。
問4(4)に関して、この運動を単振動とみなした時の「点Dから点Cまでにかかる時間」を答えます。
ポイントは「単振動の運動方程式」です。
運動方程式を書けば「角振動数」が求まります。よって、角振動数から周期Tがわかり、点C→点Dにかかる時間はT/4です。
- 小物体の円弧方向の加速度をαとすると
円弧方向の運動方程式より
mα=F=-mg/r・x
∴ α=-g/r・x - よって、この単振動は
振動中心:x=0
角振動数:ω=√(g/r)
周期:T=2π/ω=2π√(g/r)
となる - 点D→点Cにかかる時間はT/4なので
T/4=π/2・√(r/g)
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
大問2
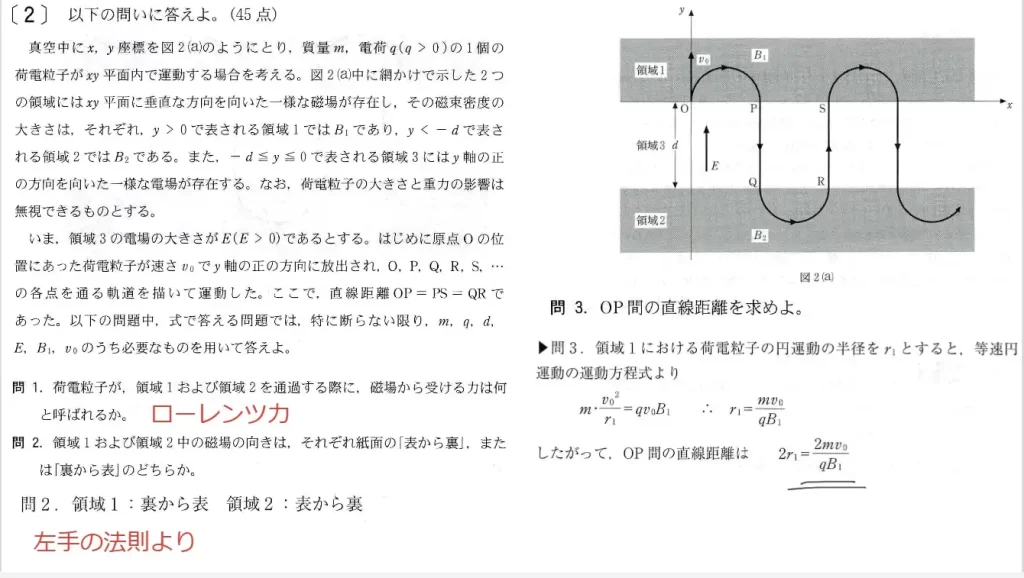
問1に関して、移動する電荷が磁場から受ける力の名前は「ローレンツ力」が正解です。
問2に関して、領域1・2における「磁場の向き」を答えます。
ポイントは「左手の法則」です。
粒子が受けるローレンツ力は、常に円運動の中心向きなので、左手の法則を使えます。
- 領域1・2において左手の法則より
領域1:裏から表向き
領域2:表から裏向き
(これが正解です)
問1・問2ともに不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、OP間の「直線距離」を答えます。
ポイントは「粒子の円運動」です。
「OPの直線距離=円運動の直径」で求まります。
- 領域1における
荷電粒子の円運動の半径をr₁とすると
運動方程式より
m・v₀²/r₁=qv₀B₁
∴ r₁=mv₀/qB₁…① - 今、OPの直線距離は2r₁なので
2r₁=2mv₀/qB₁
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4に関して、荷電粒子が「OPの軌道を描くのに要する時間」を答えます。
ポイントは「速さ×時間=距離」です。
- OP間の軌道における
OPの長さ:πr₁
荷電粒子の速さ:v₀
より
求める時間t₁とおくと
v₀×t₁=πr₁…② - ①②より
t₁=πm/qB₁…③
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問5に関して、荷電粒子がOP間の軌道を描く際に「磁場が荷電粒子にする仕事」を答えます。
ポイントは「ローレンツ力の向き」です。
左手の法則より、荷電粒子の進行方向に対して「常に垂直」です。
- ローレンツ力の向きは
荷電粒子の進行方向に対して常に垂直なので
仕事は0
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問6に関して、荷電粒子が点Pから点Qに向かって運動する時の「加速度の大きさと向き」を答えます。
ポイントは「運動方程式」です。
荷電粒子にかかる力が求まり、加速度を求めたいので、運動方程式を使います。
- 荷電粒子のy軸方向への加速度をaとおくと
運動方程式より
ma=qE
∴ a=qE/m…④、y軸正の向き
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問7に関して、荷電粒子が点Qに達した時の「速さ」を答えます。
ポイントは「等加速度直線運動」です。
問6でPQ間の加速度を求めたので、これを活用します。
- 点Qにおける荷電粒子の速さをvQとおくと
等加速度直線運動の式より
vQ²-v₀²=2ad…⑤ - ④⑤より
v₀=√(v₀²-2qEd/m)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問8に関して、領域2の「磁束密度の大きさ」を答えます。
ポイントは、問題文の条件「OP=PS=QR」です。
これにより、領域2における円運動の半径も領域1と同じr₁とわかります。
- 条件
OP=PS=ORより
領域2における荷電粒子の円運動の半径は
r₁となる - よって
領域2における荷電粒子の運動方程式より
m・v₀²/r₁=qvQB₂ - 上式に①を代入して
B₂=mvQ/qr₁
=vQ/v₀・B₁
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問9に関して、ここでシチュエーションが変わります。荷電粒子が点Qで引き返す様に電場の強さを変えた時の「電場の強さE’」を答えます。
ポイントは「点Qでの速さ=0」です。
荷電粒子が領域2に入らず引き返すという事は、荷電粒子の速さが点Qで0になるということです。
- 領域3における荷電粒子の
y軸方向の加速度をa’とおくと
運動方程式より
ma’=qE’
∴ a’=qE’/m…⑥ - 等加速度直線運動の式より
0²-v₀²=2a’(-d)…⑦ - ⑥⑦より
E’=mv₀²/2qd
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問10に関して、荷電粒子が点Pから「点Qに到達する時間」を答えます。
ポイントは「等加速度直線運動」です。
- 荷電粒子の点Pにおける初速v₀
加速度a’
より、点Qまでの時間をt’として
v₀-a’t’=0…⑧ - ⑥⑧より
t’=2d/v₀…⑨
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問11に関して、荷電粒子の「x軸方向の平均速度」を答えます。
ポイントは「直径と半円の関係」です。
実際の荷電粒子は
- 点P→点Q
- 点Q→点P
- 円弧PS
という順序で移動しますが、これを「点P→点Sへの等速直線運動」とみなします。よって「平均の速さ×1~3の時間=PS」という式が成り立ちます。
- ③⑨より
荷電粒子が点P→点Sへかかる時間は
t₁+2t’ - ①より
PSの直線距離は2r₁ - よって、平均の速さをv*とおくと
v*×(t₁+2t’)=2r₁
∴ v*=2mv₀²/(πmv₀+4qB₁d)
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
大問3
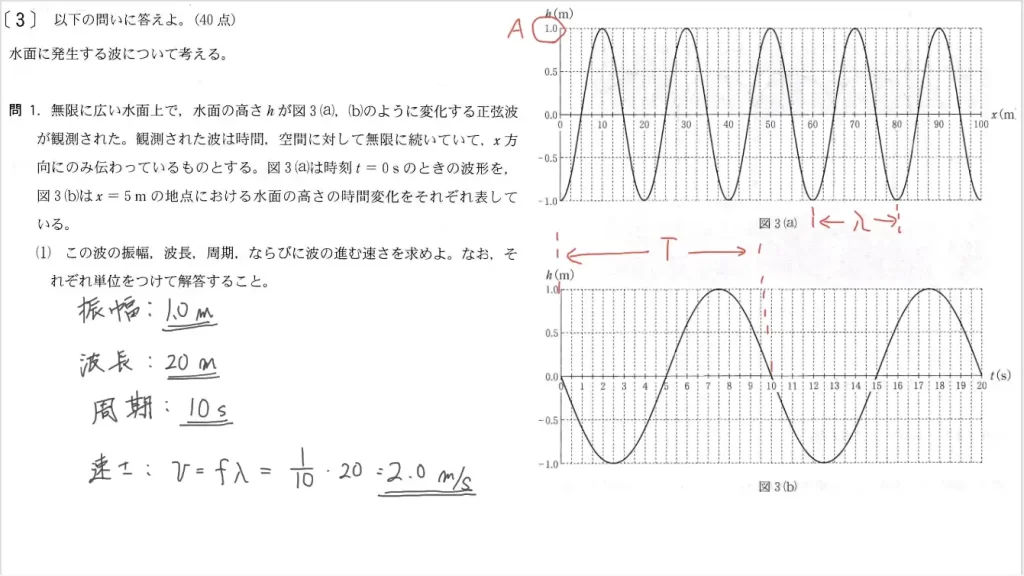
問1(1)に関して、図で示された波の「振幅、波長、周期、速さ」を答えます。
正解と根拠の関係は以下のとおりです。
| 根拠 | 正解 | |
|---|---|---|
| 振幅 | 図3aの縦の長さ | 1.0m |
| 波長 | 図3aの1波長 | 20m |
| 周期 | 図3bの1周期分 | 10s |
| 速さ | v=fλ=λ/T | 2.0m/s |
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、波の高さに関する「式h(x,t)」を答えます。
波の式の導出
- y=Asinωt…①
- ωT=2πなので
ω=2π/T…② - ②を①に代入して
y=Asin2πt/T…③ - ③の波が
t₁秒後に
右へxだけ移動すると仮定すると
③式は
y=Asin{2π(t-t₁)/T}…③’ - また
「速さ×時間=距離」より
v×t₁=x
∴ t₁=x/v…④ - ④を③’に代入して
y=Asin{2π(t-x/v)/T}
=Asin{2π(t/T-x/vT)}…⑤ - ここで
vT=λ…⑥
なので
⑥を⑤へ代入して
y=Asin{2π(t/T-x/λ)}
初期位相φ₀を加えて
y=Asin{2π(t/T-x/λ)+φ₀}
- 与式より
h(x,t)
=asin{2π{(x+b)/c+t/d}}
=asin{2π(t/d-x/(-c))+2πb/c}…① - また、x軸正の向きに進む正弦波の式は
h(x,t)=Asin{2π(t/T-x/λ+φ₀}…② - ①②を比較して
| 正解 | |
|---|---|
| a | 1.0(m) |
| d | 10(s) |
| c | -20(m) |
| b | 5.0(m) |
合格者さんでも正解が難しいレベルです。
よって、正解できれば他者に差をつける1問です。
問2(1)に関して、直立壁で反射した「反射波の式」を答えます。
- 入射波の式h(x,t)に対し
反射波の式はh(-x,t)となるため
これをhr(x,t)とおくと
hr(x,t)=h(-x,t)
=Acos{2π(-x/λ-t/T)-δ₀}
=Acos{2π(x/λ+t/T)+δ₀}…③ - ③と問題文の式を比較して
| 正解 | |
|---|---|
| D | A |
| E | x/λ+t/T |
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、知識問題です。問題文の空所(ⅰ)(ⅱ)に入る「適切な語句」を2択から答えます。
- 水面上の入射波は直立壁で水面が上下に動ける
「ⅰ:自由端」反射する - よって、壁の位置で定常波は「ⅱ:腹」を示す。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、問2(1)(2)で扱った入射波・反射波を合成した「定常波H(x,t)の式」を答えます。
ポイントは「和積の公式」です。
求める合成はH(x,t)の式は、入射波・反射波の式を単純に足し合わせれば求まります。よって必要となるのは「三角関数の公式」となります。
- H(x,t)=h(x,t)+hr(x,t)
=Acos{2π(x/λ-t/T)}+Acos{2π(x/λ+t/T)+δ}
=2Acos(2πx/λ+δ/2)cos(2πt/T+δ/2)…④ - ④と問題文の式を比較して
| 正解 | |
|---|---|
| F | 2A |
| G | 2πx/λ+δ/2 |
| K | 2πt/T+δ/2 |
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(4)に関して、「δ=2π(n+P/λ)」と表した時の「P」を直立壁の座標「x=xw」を使って答えます。
ポイントは「直立壁の位置で、定常波が腹になること」です。
定常波の「振幅が最大となるようなδの式」を立てれば正解できます。
- ④より
x=xwにおける定常波の振幅は
2A|cos(2πxw/λ+δ/2)|
となる - ところで、x=xwにおいて
定常波は腹となるので
振幅は最大となるため
|cos(2πxw/λ+δ/2)|=1
∴ 2πxw/λ+δ/2=nπ(n=0,±1,±2,…)
∴ δ=2π(n-2xw/λ)…⑤ - ⑤と問題文の式を比較して
P=-2xw
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(5)に関して、n=0における「ある位置での定常波の最大値Hmax」と「直立壁の位置での定常波の最大値Hwmax」の比を答えます。
問2(4)で求めた⑤式にn=0を代入すると、δが求まります。そのδを④式に代入すると、Hmaxが求まります。このHmaxにx=xwを代入すれば、Hwmaxが求まります。
- ⑤においてn=0とすると
δ=-4πxw/λ…⑥ - ④と⑥より
Hmax=2A|cos(2πx/λ-4πxw/2λ)|
=2A|cos2π{(x-xw)/λ}|…⑦ - ⑦においてx=xwとすると
Hwmax=2A…⑧ - よって、求める値は
Hmax/Hwmax=⑦/⑧
=|cos2π{(x-xw)/λ}|
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(6)に関して、0≦x≦xwの範囲に定常波の節が3つある時に「xwが満たすべき条件」を答えます。
- 定常波の節では振幅が常に0となるので
⑦より
2A|cos2π{(x-xw)/λ}|=0
∴ 2π|x-xw|/λ=(n+1/2)π(n=0,1,2,…)
∴ |x-xw|=(n+1/2)・λ/2…⑧
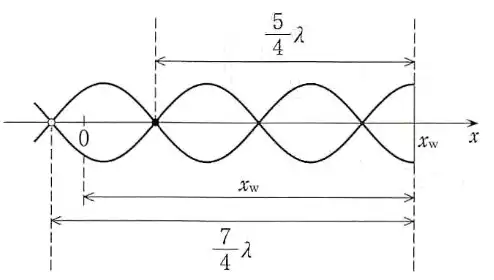
- 上図と⑧より
5λ/4≦xw<7λ/4
(これが正解です)
合格者さんでも一定数の不正解者が出るレベルです。
よって、正解できれば他者に差をつける1問です。
九州大学の物理2012年・平成24年度
大問1

問1(1)に関して、物体が静止した時の「バネの伸びd₁」を答えます。
ポイントは「力のつり合い」です。
「(小物体が)静止した」と書いてあるので、小物体にかかる力はつり合っています。
- 小物体の斜面方向の力のつり合いより
mgsinθ=kd₁
∴ d₁=mgsinθ/k…①
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、振動する小物体の
- 振幅A
- 周期T
- 速さの最大値vmax
を答えます。
ポイントは「単振動」です。
バネの付いた小物体が「振動した」と書いてあるので単振動です。
よって、運動方程式を立てようという発想になります。
- つり合いの位置をx=0とし
斜面下方にx軸をとる - 物体の斜面方向の加速度をαとおくと
運動方程式より
mα=mgsinθ-k(x+d₁)
∴ α=gsinθ-k(x+d₁)/m…② - ①②より
α=-k/m・x
となり、この運動は
振動中心:x=0
振幅:A=d₁=mgsinθ/k
角振動数:ω=√(k/m)
周期:T=2π/ω=2π√(m/k)
の単振動となる - 物体から手を放した時刻をt=0とすると
物体のx座標は
x=-Acosωt
となり
速さvは
v=Aωsinωt
となる - よって、速さの最大値は
vmax=Aω
=√(m/k)・gsinθ
(これが正解です)
不合格者さんには難しいレベルです。
合格者さんは乗り越えてくるレベルなので、合否を分ける1問です。
問1(3)に関して、小物体がバネから離れて斜面を滑り落ちた時の「Qを通過する速さvQ」を答えます。
ポイントは「バネから離れた瞬間の速さ」です。
「Pの位置でバネから離れて」と書いてあり、Pにおける小物体の速さは0です。
- 題意より、小物体は
Pの位置から初速0で斜面を滑る - 小物体の斜面方向の加速度をα₁とおくと
運動方程式より
mα₁=mgsinθ
∴ α₁=gsinθ - よって
vQ²-0²=2α₁l
∴ vQ=√(2glsinθ)…③
(これが正解です)
「初速」が少し難しいですが、不合格者さんの一定数が不正解になるぐらいです。
よって、合否を分ける1問より少し簡単な問題です。
問1(4)に関して、Qを通過した小物体に関して
- 摩擦力で減速中の加速度の大きさa
- Qを通過してから止まるまでの時間t
- その距離d₂
を答えます。
ポイントは「運動方程式」です。
細かい値を3つ答える問題なので、運動方程式から考えるのが安全・確実です。
- 斜面水平・鉛直方向の運動方程式より
m(-a)=mgsinθ-μN
0=-N+mgcosθ - a=-gsinθ+μN…④
N=mgcosθ…⑤ - ④⑤より
a=g(μcosθ-sinθ)…⑥
(これが正解です) - また
vQ-at=0…⑦
なので
③⑦より
t=1/(μcosθ-sinθ)・√{(2lsinθ)/g}
(これが正解です) - また
0²-vQ²=2(-a)d₂…⑧
なので
③⑥⑧より
d₂=lsinθ/(μcosθ-sinθ)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(5)に関して、バネをPの位置からさらにd₃押し上げて手を放した場合の「点Rを通過する速さvR」を答えます。
ポイントは「エネルギー保存則」です。
問1(4)と異なり、求める値は「Rでの速さ」のみです。ここは「エネルギー保存則」を使いましょう。
- 初期状態と点Rにおける
小物体の力学的エネルギーは
QR間で動摩擦力がした
仕事の分だけ変化するので
1/2・kd₃²+mg(2l+d₃)sinθ=1/2・vR²+μmgcosθ・l - 上式を解いて
vR=√{kd₃²/m+2g(2l+d₃)sinθ-2μglcosθ}
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(1)(2)に関して、ここでシチュエーションが変わります。小物体を斜めに投げ上げた時の
- 1回目の衝突直後の速度成分
- 2回目の衝突直後の速度成分
- n回目の衝突直後の速度成分
を答えます。
ポイントは、問題文「水平面はなめらか」です。
なめらかなので、小物体のx方向の速度成分は変化しません。
よって、y成分に関する「はね返りの式」を考えればよいと解ります。
- 小物体を投げ上げた瞬間の速度成分は
x軸方向:v₀cosα
y軸方向:v₀sinα - 速度のx成分に関して
床の水平面は滑らかなので
はね返りによる速度変化は無く
v₁x=v₀cosα
(これが正解です)
v₂x=v₀cosα
(これが正解です)
vnx=v₀cosα
(これが正解です) - 速度のy成分に関して
1回目の衝突直前の
小物体の速度のy成分は
-v₀y
なので、はね返りの式より
v₁y-0=-e(-v₀y-0)
∴ v₁y=ev₀sinα
(これが正解です) - 同様にして
v₂y=e²v₀sinα
(これが正解です) - 同様にして
vny=e^n・v₀sinα
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、「n回目の衝突にかかる時間Δtn」を答えます。
ポイントは「y軸方向の運動時間」です。
「n回目の衝突」とは、n-1回目のバウンドが着地するまでの時間であり、この間は等加速度運動となります。
- y成分の等加速度運動の式より
0=v(n-1)y・Δtn-1/2・gΔtn²
∴ Δtn≠0より
Δtn={2e^(n-1)・v₀sinα}/g…⑨
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(4)(5)に関して、n回目の衝突までに進んだ「x方向の距離xn」を答えます。
ポイントは「n回目の衝突までにかかった時間」です。
問2(1)より、速度のx成分は「v₀cosαで一定」と判っているので、かかった時間さえ判れば「速さ×時間=距離」で正解できます。
- n-1回目からn回目の衝突における
x方向の移動距離は
Δxn=v₀cosα×Δtn…(10) - ⑨と(10)より
Δxn={e^(n-1)・v₀²sin2α}/g - よって
xn=Δx₁+Δx₂+・・・+Δxn
={(e⁰+e¹+e²+・・・+e^(n-1))・v₀²sin2α}/g
=(1-e^n)/(1-e)・(v₀²sin2α)/g
(これが正解です) - また、上式でe^nとすると
xfとなるため
xf=1/(1-e)・(v₀²sin2α)/g
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(6)に関して、n回目の衝突で「小物体が失うエネルギー」を答えます。
ポイントは「失うエネルギー=衝突前-衝突後」です。
速度のx成分は変化しないので、y成分の引き算で正解できます。
- 衝突前の運動ネルギーから
衝突後の運動エネルギーを引き算して
qn=1/2・mv(n-1)²-1/2・mvn²
=1/2・m{v(n-1)y²-vny²}…(11)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(7)に関して、n回の衝突で「小物体が失うエネルギー」を答えます。
ポイントは「式変形」です。
問2(6)で「n回目に失われるエネルギー」が求まっているので、これを「n回の合計」に拡張する式変形を行えばよいです。
- (11)より
Qn=q₁+q₂+・・・+qn
=1/2・m{(v₀y²-v₁y²)+(v₁y²-v₂y²)+・・・+(v(n-1)y²-vny²)
=1/2・m(v₀y²-vny²)
=1/2・m(1-e^2n)・(v₀sinα)² - 題意より、e^n=0とすると
QnはQfとなるので
Qf=1/2・m(v₀sinα)²
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
大問2
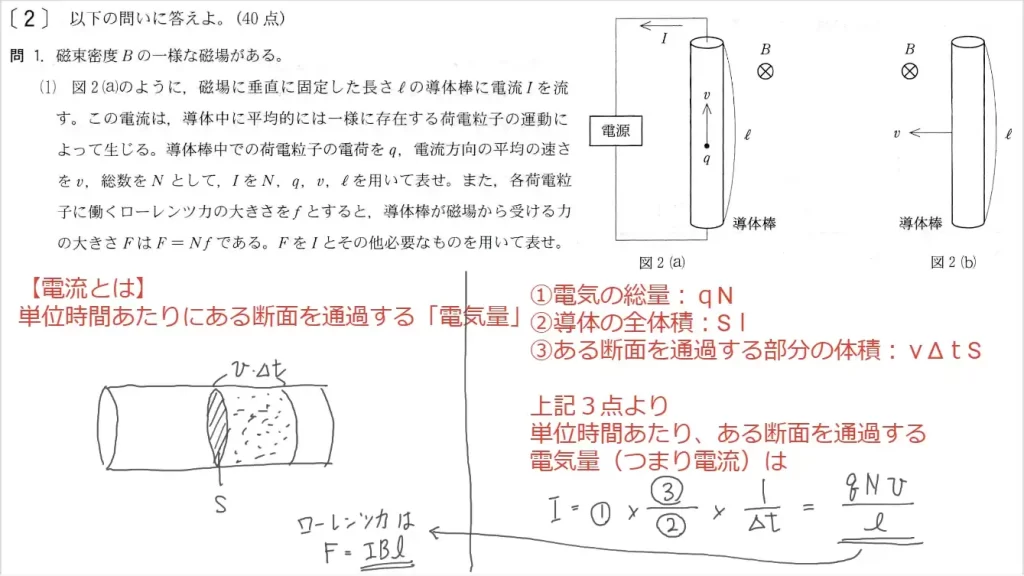
問1(1)に関して、導体棒に電流を流した時の「電流の大きさ」および、その導体棒を横に動かした時の「導体棒が磁場から受ける力の大きさ」を答えます。
ポイントは「電流の定義」です。
【電流の定義に基づいた考え方】
電流とは、導線の断面を1秒間に通過する電気量
- 導体棒の断面積をSとすると
題意より
導体棒の総電気量:qN…①
導体棒の体積:Sl…②
となる - 今、導体棒のある断面を
Δt秒間に通過する電子が
含まれる部分の体積は
vΔt・S…③
である - よって、単位時間あたりに
導体棒のある断面を通過する電気量
すなわち電流は
I=①×③/②×1/Δt
=qNv/l
(これが正解です)
不合格者さんの一定数は不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(2)に関して、ローレンツ力によって導体棒の電子が移動してできた「電場の強さ」を答えます。また、それによる「誘導起電力の大きさ」を答えます。
ポイントは「力のつり合い」です。
問題文に「電場による力と磁場による力がつり合った」と書いてあるので、「qE=qvB」という関係が成り立っています。
- ローレンツ力によって
移動した電子が作る電場から
荷電粒子が受ける力の大きさは
qE
である - 題意より
上記の力とローレンツ力がつり合うので
qE=qvB
∴ E=vB
(これが正解です) - また、誘導起電力の大きさVは
V=El=vBl
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(1)に関して、ここでシチュエーションが変わります。地面に鉛直に立てられた長方形の回路から、導体棒が落下を始めた時の「誘導電流の向き」を答えます。
ポイントは「レンツの法則」です。
【レンツの法則】
回路を貫く磁束の変化を妨げる方向に誘導起電力が発生する
- 導体棒の落下により
閉回路pXYspを貫く磁束は増加する - よって
回路を貫く磁束を減らす方向に
誘導電流が流れるため
「XからY」方向となる
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)(a)に関して、時刻tにおける「コンデンサーの電荷」を答えます。
ポイントは「誘導起電力」です。
コンデンサーの静電容量はCと判っているので、電圧が求まれば「Q=CV」よりQが求まります。今、この回路における「電圧」とは、導体棒の落下による「誘導起電力」なので・・・という流れです。
- 問1(2)より
導体棒に発生する誘導起電力Vは
V=vBl…④
である - これがコンデンサーの
極板間電圧となるので
Q=CV…⑤ - よって、④⑤より
Q=vBlC
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(2)(b)に関して、上記における「誘導電流I’」を答えます。
- 問2(2)(a)より
Q=vBlC
なので
ΔQ=BlC・Δv…⑥ - また、電流の定義より
I’=ΔQ/Δt…⑦
速度・加速度の関係より
Δv=a・Δt…⑧ - よって⑥⑦⑧より
I’=CBIa…(A)
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(3)に関して、導体棒の下側に生じる回路(XYrqX)に流れる「電流I」を答えます。
- コイルにかかる電圧をVとすると
V=L・ΔI/Δt…⑨ - この電圧Vは
導体棒の落下で生じる
誘導起電力に等しので
④⑨より
L・ΔI/Δt=vBl
∴ ΔI=vΔtBl/L
=Bl/L・Δx - 両辺を積分して
I=Bl/L・x+C₁(C₁は積分定数)…(10) - 題意より
x=0の時I=0を(10)に代入して
C₁=0 - ゆえに
I=Bl/L・x…(B)
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(4)に関して、I’とIを使って「導体棒の運動方程式」を答えます。
ポイントは「ローレンツ力」です。
導体棒にはI+I’の電流が流れるため、磁場から受ける力が上向きにかかります。
- 導体棒にはX→Yの向きに
I+I’の電流が流れているため
磁場からの力
(I’+I)Bl
をx軸負方向に受けている - よって、導体棒の運動方程式は
Ma=Mg-(I’+I)Bl…(C)
(これが正解です)
問2(3)までを正解できずとも、本問単独で正解できます。
よって、不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問2(5)に関して、(4)で求めた運動の(単振動の)「角振動数ω」と「振動中心の座標x₀」を答えます。
ポイントは「式変形」です。
(4)の運動方程式を「単振動の式」に変形すれば正解できます。
- (A)(B)を(C)に代入すると
Ma=Mg-(CBla+Bl/L・x)Bl
∴ a=-B²l²/{L(M+CB²l²)}・(x-LMg/B²l²) - よって、上式より
導体棒は単振動しており
角振動数:ω=Bl/√{(M+CB²l²)L}
振動中心:x₀=MgL/B²l²…(11)
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(6)に関して、Iのとる「最小値・最大値」を答えます。
- コイルの電圧と
導体棒の落下による誘導起電力の関係より
L・ΔI/Δt=vBl…(D) - Iが最大値・最小値になる瞬間は
ΔI/Δt=0
なので
(D)の右辺より
v=0
となる - ここで導体棒の運動について考えると
v=0
となるのは、単振動の
上端:x=0
下端:x=2x₀
である - 今(B)において
x=0とすると
I=0
(これが正解です)
となり、これはIの最小値を示す - また(B)において
x=2x₀とすると
I=Bl/L・2x₀
=Bl/L・2MgL/B²l²(∵(11))
=2Mg/Bl
(これが正解です)
となり、これはIの最大値を示す
合格者さんでも一定数の不正解が出るレベルです。
よって、合否を分ける1問より少し難しい問題です。
大問3
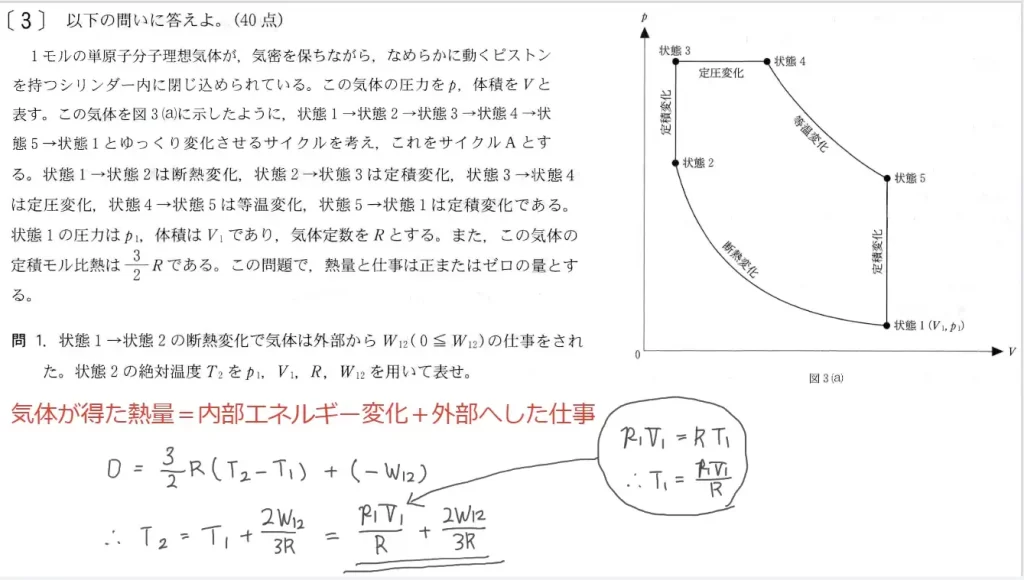
問1に関して、状態1→状態2の断熱変化で気体が外部からW₁₂の仕事をされた時の「状態2の温度T₂」を答えます。
ポイントは「熱力学第一法則」です。
- 熱力学第一法則より
0=3/2・R(T₂-T₁)+(-W₁₂)…① - また、状態1における状態方程式より
p₁V₁=RT₁…② - ①②よりT₁を消去すると
T₂=p₁V₁/R+2W₁₂/3R
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2に関して、状態3と状態2の「絶対温度の差、T₃-T₂」を答えます。
ポイントは「熱力学第一法則」です。
- 熱力学第一法則より
Q₂₃=3/2・R(T₃-T₂)+0
∴ T₃-T₂=2Q₂₃/3R
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、状態3→状態4の定圧変化で熱量Q₃₄(≧0)の移動があった時の「正しい選択肢」を3択から選びます。
ポイントは「熱力学第一法則」です。
| 選択肢 | 正誤 | 根拠 | |
|---|---|---|---|
| 1 | Q₃₄は気体が吸収した熱量である | ○ | pVグラフにおいて温度が上がるほどグラフは原点から右上に遠ざかる |
| 2 | Q₃₄=0である | × | 外部に仕事をした上、内部エネルギーも増えているので、Q₃₄は正の値である |
| 3 | Q₃₄は気体が放出した熱量である | × | 同上 |
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問4に関して、状態1~5の絶対温度をT₁~T₅とする時、それらの関係を「正しく表した選択肢」を6択から選びます。
ポイントは「pVグラフの読み方」です。
pVグラフでは、気体の温度が高いほど等温線が「原点から右上に」離れていきます。
- pVグラフでは温度が高いほど
等温線が原点から右上に離れていくので
T₁~T₅で温度が最も高いのは
T₄=T₅である - よって、6つの選択肢の中で
T₄=T₅が右端にある
①か④が正解となる - 問1より
T₁<T₂なので
正解は選択肢④となる
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問5に関して、ここでシチュエーションが変わります。状態5からの断熱変化「状態6」が追加された時、状態5→状態6で気体の温度が「上がるか、下がるか、変化しないか」を答えます。
ポイントは「断熱変化」です。
- 状態5→状態6において
断熱変化で体積が増加しているので
温度は下がる - よって、正解のグラフは
X(温度が低下)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問6に関して、サイクルA(状態1→2→3→4→5→1)における「状態5→状態1で放出した熱量Q₅₁」を答えます。
ポイントは「正解に使う文字」です。
| 使う文字 | 経路 |
|---|---|
| W₅₆ | 状態5→状態6 |
| Q₅₁ | 状態5→状態1 |
| Q₆₁ | 状態6→状態1 |
よって、上記3つの経路に関して立式し、まとめれば正解できると解ります。
- 状態5→状態6に関して
熱力学第一法則より
0=3/2・R(T₆-T₅)+W₅₆
∴ T₆-T₅=-2W₅₆/3R…③ - 状態6→状態1に関して
定圧モル比熱は5/2・Rより
-Q₆₁=5/2・R(T₁-T₆)
∴ T₁-T₆=-2Q₆₁/5R…④ - 状態5→状態1に関して
熱力学第一法則より
-Q₅₁=3/2・R(T₁-T₅)+0
∴ T₁-T₅=-2Q₅₁/3R…⑤ - よって
⑤の左辺=③の左辺+④の左辺
より
-2Q₅₁/3R=-2Q₆₁/5R-2W₅₆/3R
∴ Q₅₁=W₅₆+3/5・Q₆₁
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問7に関して、状態6→状態1の定圧変化において「気体が外部からされた仕事W₆₁」を答えます。
ポイントは「熱力学第一法則」です。
- 熱力学第一法則より
-Q₆₁=3/2・R(T₁-T₆)-W₆₁
④を代入してまとめると
W₆₁=2/5・Q₆₁
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問8に関して、サイクルAとBの「熱効率」を答えます。
- サイクルAに関して
1サイクルによって温度は元に戻るので
内部エネルギーは変化しない - よって、サイクルAにおいて
熱力学第一法則より
(Q₂₃+Q₃₄+Q₄₅-Q₅₁)=0+(-W₁₂+W₃₄+W₄₅)…⑥ - 熱効率eAは
eA=(-W₁₂+W₃₄+W₄₅)/(Q₂₃+Q₃₄+Q₄₅)
=(Q₂₃+Q₃₄+Q₄₅-Q₅₁)/(Q₂₃+Q₃₄+Q₄₅)
=1-Q₅₁/(Q₂₃+Q₃₄+Q₄₅)…⑦
(これが正解です) - 同様にサイクルBにおいて
熱力学第一法則より
(Q₂₃+Q₃₄+Q₄₅-Q₆₁)=0+(-W₁₂+W₃₄+W₄₅+W₅₆-W₆₁)…⑧ - 熱効率eBは
eB=(-W₁₂+W₃₄+W₄₅+W₅₆-W₆₁)/(Q₂₃+Q₃₄+Q₄₅)
=(Q₂₃+Q₃₄+Q₄₅-Q₆₁)/(Q₂₃+Q₃₄+Q₄₅)
=1-Q₆₁/(Q₂₃+Q₃₄+Q₄₅)…⑨
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、全ての受験生さんが正解したい問題です。
問9に関して、「Q₅₁-Q₆₁」を答えます。
- ⑧-⑥より
Q₅₁-Q₆₁=W₅₆-W₆₁…(10)
(これが正解です)
本問自体は簡単ですが、本問に参加するには問8の正解が必要です。
よって、問8とセットで、合否を分ける1問です。
問10に関して、W₅₆とW₆₁の「正しい関係」を3択から答えます。
- 気体がした仕事は
pVグラフとV軸が作る面積なので
図3(b)より
W₅₆>W₆₁…(11)
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、全ての受験生さんが正解したい問題です。
問11に関して、eAとeBの「正しい関係」を3択から答えます。
- (10)(11)より
Q₅₁-Q₆₁>0
∴ Q₅₁>Q₆₁…(12) - ⑦⑨(12)より
eA<eB
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、全ての受験生さんが正解したい問題です。
九州大学の物理2010年・平成22年度
大問1
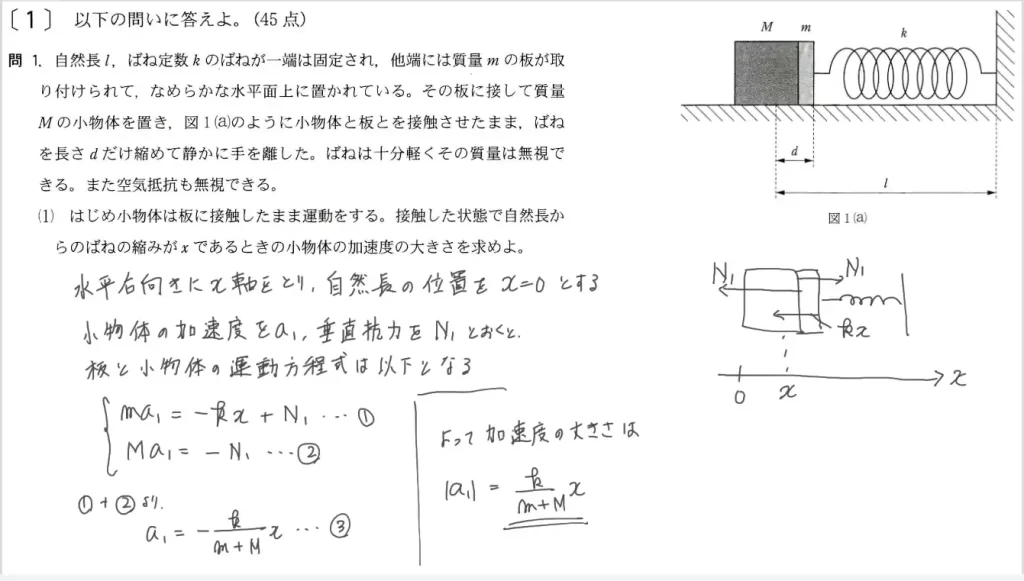
問1(1)に関して、小物体と板が接触して運動する時の「小物体の加速度の大きさ」を答えます。
ポイントは「運動方程式」です。
「加速度」を求められているので、運動方程式を使います。
- 水平右向きにx軸をとり
バネの自然長の位置をx=0とする - 小物体の加速度をa₁
垂直抗力をN₁
とおく - 板の運動方程式は
ma₁=-kx+N₁…①
小物体の運動方程式は
Ma₁=-N₁…②
となる - ①+②より
a₁=-kx/(m+M)…③ - よって、加速度の大きさは
|③|=kx/(m+M)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(2)に関して、「小物体が板から離れるまでの時間」を答えます。
ポイントは「垂直抗力」です。
板と小物体が離れる瞬間に「垂直抗力N₁=0」となります。
- ①に③を代入して
N₁についてまとめると
N₁=Mkx/(m+M)
となる - 小物体が板から離れる条件は
N₁=0
であり、この時のx座標は
x=0
である - ③の単振動においてx=0となる時間は
周期をT₁とおくと
T₁/4
であり、③より角振動数ω₁とすると
ω₁=√{k/(m+M)}
なので
T₁/4=π/2・√{(m+M)/k}
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(3)に関して、小物体が板から離れた直後の「速度の大きさ」を答えます。
ポイントは「力学的エネルギー保存則」です。
小物体と板は、離れるまで一体として運動するので、バネの弾性エネルギーと運動エネルギーが保存します。
- 小物体が板から離れた直後の速度をv₁とおくと
力学的エネルギー保存則より
1/2・kd²=1/2・(m+M)v₁²
∴ v₁=d√{k/(m+M)}
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(1)に関して、ここでシチュエーションが変わります。先程までの床面が斜度θの斜面になった時、つりあいの位置における「バネの伸びx₀」を答えます。
- 斜面方向の力のつり合いより
mgsinθ=kx₀
∴ x₀=(mgsinθ)/k…④
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、小物体と板が離れた時の「バネの伸びs」を答えます。
ポイントは「垂直抗力」です。
問1(2)と同様、運動方程式を立て「垂直抗力=0」とした時の「x座標」が、小物体と板が離れる位置です。その位置と「バネの自然長の位置」を比べれば「バネの伸び」が求まります。
- 斜面上向きにx軸をとり
バネの自然長の位置をx=0とおく - バネの縮みをx
加速度をa₂とした時の
板の運動方程式は
ma₂=-kx-mgsinθ+N₂…⑤
小物体の方程式は
Ma₂=-N₂-Mgsinθ…⑥ - ⑤⑥よりa₂を消去して
N₂=Mkx/(m+M) - 小物体と板が離れる条件は
N₂=0
なので、この時のx座標は
x=0
となる - よって、小物体と板が離れる位置と
バネの自然長の位置が等しいため
s=0
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(3)に関して、板から離れた直後の小物体の「速度の大きさ」を答えます。
ポイントは「力学的エネルギー保存則」です。
- 板と小物体が離れた直後の速さをv₂とおくと
力学的エネルギー保存則より
1/2・kD²+(m+M)gDsinθ=1/2・(m+M)v₂²
∴ v₂=√{kD²/(m+M)+2gDsinθ}…⑦
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(4)に関して、小物体と離れた板が行う単振動の「振幅」を答えます。
ポイントは「運動方程式」と「力学的エネルギー保存則」です。
| 求まるもの | |
|---|---|
| 運動方程式 | 振動中心 |
| 力学的エネルギー保存則 | 最下点 |
「振動中心+振幅=最下点」なので、上記2式を立てればよいと解ります。
- 板の加速度をa₂’として
バネの縮がxの時の運動方程式を立てると
ma₂’=-kx-mgsinθ
∴ a₂’=-k/m・{x+(mgsinθ)/k) - よって、この運動は
角振動数:ω₂’=√(k/m)…⑧
振動中心:x=-(mgsinθ)/k=-x₀(∵④)
の単振動である - 振幅をAとし
板が小物体と離れた位置と板の最下点で
力学的エネルギー保存則を用いると
1/2・mv₂²=1/2・k(x₀+A)²-mg(x₀+A)sinθ…⑨ - ここで④より
sinθ=kx₀/mg…④’ - ⑨に④’と⑦を代入して
A=(計算略)
=2x₀
(これが正解です)
合格者さんでも一定数の不正解が出るレベルです。
よって、正解できれば他者に差をつける1問です。
問2(5)に関して、
- 小物体が板から離れた位置が
振動中心と振動上端の真ん中なので
求める時間は2/3周期分となる - よって、周期T’として
2/3・T’
=2/3・2π/ω₂’
=4π/3・√(m/k)(∵⑧)
(これが正解です)
合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し難しい問題です。
大問2
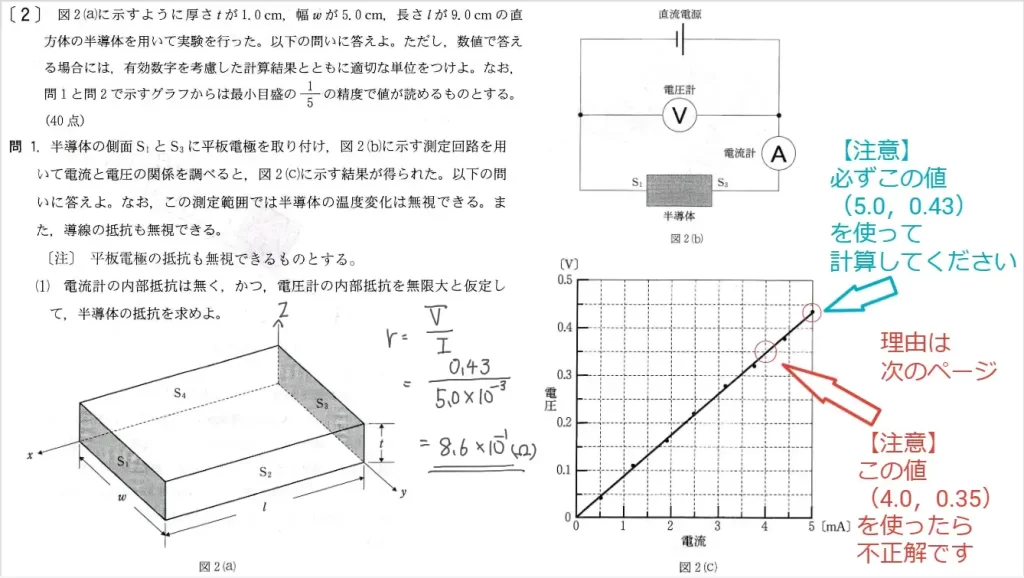
以下、単位を省略しております。
回答の際は単位をつけてください。
問1(1)に関して、図に示された「半導体の抵抗」を答えます。
ポイントは「オームの法則」です。
図2(c)で電圧-電流グラフが与えられているので、電圧・電流の値を読みとり「V=IR」に代入すれば正解です。
グラフを見ると点(4.0 , 0.35)が読み取りやすく、値もほど良く大きいですが、これを使うと不正解になります。
グラフからデータを読み取る際は「誤差」をできるだけ小さくするために「できるだけ大きな値」で読み取る必要があります。
| 目盛りの最小 | 誤差 (4.0,0.35) | 誤差 (5.0,0.43) |
|---|---|---|
| 0.1mA | 0.1÷4.0 =2.5% | 0.1÷5.0 =2.0% |
| 0.01V | 0.01÷0.35 ≒2.9% | 0.01÷0.43 ≒2.3% |
- 図2(c)のグラフより
(I,V)=(5.0,0.43) - 半導体の抵抗をrとすると
オームの法則より
r=V/I=8.6×10⁻¹
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問1(2)に関して、図2(b)の回路における「半導体の抵抗」を答えます。
ポイントは「キルヒホッフの第二法則」です。
【キルヒホッフの第二法則】
任意の閉回路を一定の方向にたどると、その電圧の総和は0になる
- 電流・電圧の値に
(5.0mA,0.43V)を用い
電流計の内部抵抗をrA
半導体の抵抗をr’
とおく - キルヒホッフの第二法則より
0.43-5.0×10⁻³(rA+r’)=0
∴ r’=84.8≒8.5×10
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(3)に関して、この半導体の「抵抗率」を答えます。
ポイントは「抵抗の式」です。
【抵抗の式】
R=ρ・l/S
- R:抵抗
- ρ:抵抗率
- l:長さ
- S:断面積
上式に出てくる「ρ」が抵抗率です。
- 求める抵抗率をρとおくと
抵抗の式より
r’=ρ・l/wt - よって
ρ=r’・wt/l
=0.471
≒4.7×10⁻¹
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(1)に関して、ここでシチュエーションが変わります。図2(d)に示す半導体を磁場に入れて電流を流した時、「面S₂とS₄のどちらが低電位になるか」を答えます。
ポイントは「左手の法則」です。
キャリアが自由電子なので、ローレンツ力が生じます。その方向は「左手の法則」でわかります。
- 左手の法則より
半導体内の自由電子は
S₄ → S₂方向にローレンツ力を受け
S₂側に集まる - よって、S₄ → S₂へ磁場が発生するため
電位が低いのは「S₂」となる
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、半導体中の「自由電子の平均の速さ」を答えます。
ポイントは「力のつり合い」です。
半導体中では、自由電子に働く「ローレンツ力」と「電場から受ける力」がつり合っています。このつり合いの式の中に、求める「平均の速さ」が含まれています。
- 以下の様に置いて考える
| S₂・S₄間の電圧 | Vy |
| S₂・S₄間の電場 | E |
| 電子の電荷 | e |
| 磁束密度 | B |
| 自由電子の平均の速さ | v |
- 半導体中では
磁場によるローレンツ力と
S₂・S₄間の電場から受ける力が
つり合っているので
eE=evB…① - また
E=Vy/w…②
なので、①②より
v=Vy/wB
=0.156
≒1.6×10⁻¹
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(3)に関して、半導体中の自由電子の「個数密度」を答えます。
ポイントは「電流の定義」です。
【電流の定義に基づいた考え方】
電流とは、導線の断面を1秒間に通過する電気量
この考えに沿って立式すると「電流=電子1個の電気量×個数密度×1秒間の通過体積」となり、求める「個数密度」が出てきます。
- x軸性方向の電流をIx
個数密度をnとおくと
Ix=envwt
∴ n=Ix/evwt
≒6.4×10²⁰
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
大問3

以下、単位を省略して書きます。
回答の際は単位を付けてください。
問1(ア)に関して、救急車が点Aで発した音が「測定器に到達するまでの時間」を答えます。
ポイントは「速さ×時間=距離」です。
- 点A~測定器までの距離:l
音波の速さ:V
より
求める時間をtAと置くと
tA=l/V
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(イ)に関して、救急車が点Bで発した音が「測定器に到達するまでの時間」を答えます。
ポイントは「AB間の距離」です。
音波が進む距離は、(ア)に比べAB間だけ短くなっています。
- 点B~測定器までの距離:l-Vs
音波の速さ:V
より
求める時間をtBとおくと
tB=(l-VsΔt)/V
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(ウ)に関して、点Aで発射した音波が測定器に届いた後「点Bで発射した音波が測定器に届くまでの時間」を答えます。
ポイントは「時刻」です。
「Bで発射した音」の方が、後で測定器に届くので、正解は「Bの音波が届いた時刻-Aの音波が届いた時刻」となります。
- 救急車がAで音波を出した時刻をt=0とすると
A発の音波:時刻tAに測定器へ到達
B発の音波:時刻Δt+tBに測定器へ到達
となる - よって、求める時間は
(Δt+tB)-tA
=(V-Vs)Δt/V
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(エ)に関して、測定器が測定した「音波の振動数」を答えます。
ポイントは「振動数=1秒間の音波の個数」です。
よって、以下の様な表で考えると、簡単に正解できます。
| 時間 | 音波の個数 |
|---|---|
| (ウ)秒間 | fΔt個 |
| 1秒間 | (エ)個 |
- 上表より、求める振動数をfM’とおくと
fM’=fΔt÷(ウ)
=Vf/(V-Vs)
(これが正解です)
不合格者さんでも正解してくるレベルです。
よって、全ての受験生さんが正解したい問題です。
問2(オ)に関して、ここでシチュエーションが変わります。測定器が救急車に対して斜めにある時の「線分OCの長さ」を答えます。
ポイントは、問題文「線分ODと線分OHの長さが等しいと見なせる」です。
これにより、OHの長さはLとなります。残ったCHはCDcosθなので・・・という流れです。
- 題意より
OH=OD
とみなせるので
OC=OH+CH
=OD+CH
=L+CDcosθ
=L+VsΔtcosθ
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(カ)に関して、Cで発せられた音波が「測定器に届くまでの時間」を答えます。
ポイントは「速さ×時間=距離」です。
OCの長さは(オ)で求めたので、音速Vで割れば正解です。
- 求める時間をtcとおくと
tc=OC/V
=(L+VsΔtcosθ)/V
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(キ)に関して、点Cで発射した音波が測定器に届いた後「点Dで発射した音波が測定器に届くまでの時間」を答えます。
ポイントは「時刻」です。
「Dで発射した音」の方が、後で測定器に届くので、正解は「Dの音波が届いた時刻-Cの音波が届いた時刻」となります。
- 救急車がCで音波を出した時刻をt=0とすると
C発の音波:時刻tcに測定器へ到達
D発の音波:時刻Δt+tDに測定器へ到達
となる - ここで
tD=L/V
なので、求める時間Δt₀とすると
Δt₀=(Δt+tD)-tc
=(V-Vscosθ)Δt/V
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(ク)に関して、測定器が測定した「音波の振動数」を答えます。
ポイントは「振動数=1秒間の音波の個数」です。
よって、以下の様な表で考えると、簡単に正解できます。
| 時間 | 音波の個数 |
|---|---|
| (キ)秒間 | fΔt個 |
| 1秒間 | (ク)個 |
- 上表より、求める振動数をf₀’とおくと
f₀’=fΔt÷(キ)
=Vf/(V-Vscosθ)
(これが正解です)
不合格者さんでも正解してくるレベルです。
全ての受験生さんが正解したい問題です。
問3に関して、問2の測定器が測定した「音波のグラフ」を6択から答えます。
ポイントは「ドップラー効果」です。
時間t₀までは救急車が近づいて来るので、振動数は増加した状態になります。この情報だけで「グラフ②④⑤⑥が不正解」と判り、①③の2択問題になります。
- 時間t₀までは救急車が近づいて来るので
振動数が多い状態となり
グラフ①か③が正解となる - また、救急車が十分遠方にある場合
角θが非常に小さくなるため
cosθ=1
と近似でき、この時
f₀’=fM’
となる - つまり、救急車が
十分遠い場合でも
十分近い場合でも
救急車が発する音波と同じ振動数になるため
それを表すグラフ①が正解となる
(これが正解です) - また、測定器が直線Pから
非常に遠い場合を考えると
点M付近でも測定される振動数の変化は
ゆるやかになるため
これを表す曲線B(破線)が正解となる
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問4に関して、救急車が測定器に近づく時の「ピーポー音の時間間隔」を3択から答えます。
ポイントは「音の時間間隔=周期=1/振動数」です。
救急車が近づいて来るので、測定器が受け取る音波の振動数は、救急車が発するものより大きいです。
- 救急車が測定器に近づいて行くので
救急車が発する振動数<測定器が受け取る振動数
となる - よって
T₁<T₀
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
九州大学の物理2009年・平成21年度
大問1
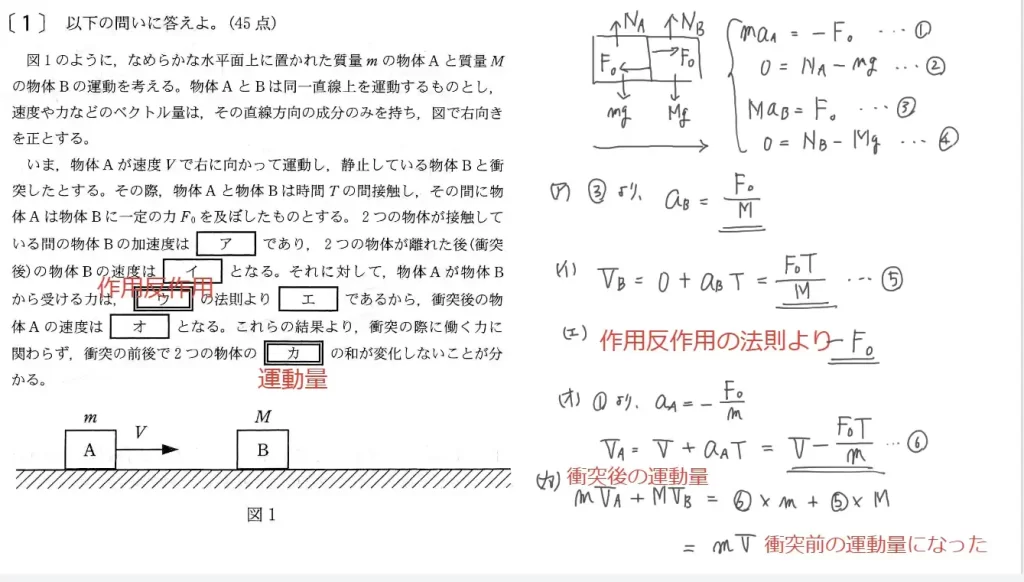
問1(ア)に関して、接触する2物体AとBにおける「物体Bの加速度」を答えます。
ポイントは「運動方程式」です。
「加速度」を問われているので、運動方程式を使うだろうと想像できます。
- 以下の様に値を設定する
| Aの加速度 | aA |
| Bの加速度 | aB |
| Aが床から受ける 垂直抗力 | NA |
| Bが床から受ける 垂直抗力 | NB |
- 物体A・Bの
水平方向・鉛直方向の運動方程式より
maA=-F₀…①
0=NA-mg…②
MaB=F₀…③
0=NB-Mg…④ - ③より
aB=F₀/M…⑤
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(イ)に関して、衝突により2つの物体が離れた直後の「物体Bの速度」を答えます。
ポイントは「等加速度直線運動」です。
物体Bの初速は0なので「加速度×時間」で速度が出ます。
- 求める速度をVBとおくと
Bの初速0より
VB=0+aBT…⑥ - ⑤⑥より
VB=F₀T/M…(ⅰ)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(ウ)(エ)に関して、物体Aが「物体Bから受ける力」を答えます。
- 物体Aが物体Bから受ける力は
「ウ:作用反作用」の法則より
「エ:-F₀」
である。
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(オ)に関して、衝突後の「物体Aの速度」を答えます。
ポイントは「等加速度直線運動」です。
問1(イ)で求めた物体Bと同様の方法で正解できます。
- ①より
aA=-F₀/M…①’ - 求める速度をVAとおくと
Aの初速Vより
VA=V+aAT…⑦ - ①’⑦より
VA=V-F₀T/m…(ⅱ)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(カ)に関して、衝突前後の2物体について「和が変化しないもの」を答えます。
ポイントは「外力」です。
A・Bが作る物体系には「外力による力積の変化」が無いため、運動量が保存します。よって、運動量が変化しないことを式で示せば正解です。
- 衝突後の2物体の運動量の和より
mVA+MVB=(ⅱ)×m+(ⅰ)×M
=mV - mVは衝突前の運動量の和なので
「カ:運動量」
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(キ)(ク)に関して、物体Aが「物体Bに及ぼした力積」を答えます。
- 力積の単位は
「キ:kg・m/s²」
である - この衝突では
物体Aが物体Bに対し
F₀の力をT秒与えているので
力積は「ク:F₀T」となる
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(ケ)(コ)に関して、小物体Aが小物体Bに及ぼした「力積が最も小さくなる場合」を考えます。
- 衝突前後の運動量保存則より
mV=mVA+MVB…⑧ - 2物体の反発係数をeとして
はね返りの式より
VA-VB=-e(V-0)…⑨ - ⑧⑨からVAwo消去して
VB=(1+e)mV/(m+M) - 力積をIBとおくと
物体Bの運動量の変化に等しいので
IB=MVB-0
=(1+e)mMV/(m+M) - よって、IBが最小となるeの値は
「ケ:e=0」
であり、この時
「コ:IB=mMV/(m+M)」
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(1)に関して、ここでシチュエーションが変わります。先程までの水平な床面が、斜度θの下り坂に変わっており、床面には摩擦が発生します。この時、物体Cが物体Dに「衝突する直前のCの速度」および「衝突の時刻」を答えます。
ポイントは「運動方程式」です。
シチュエーションが変化してますし、「速度」と「時刻」の2つを答えるので、運動方程式から地道に進めるのが安全です。
- 物体Cの加速度をaCとおくと
運動方程式より
maC=mgsinθ
∴ aC=gsinθ…(10) - 等加速度直線運動の式より
V₀²-0²=2aCX
∴ V₀=√(2gXsinθ)
(これが正解です) - また、物体Cの初速は0なので
1/2・aCt₁²=X…(11) - (10)(11)より
t₁=√(2X/gsinθ)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(2)に関して、1回目の衝突直後の「Cの速度」および「Dの速度」を答えます。
ポイントは「運動量保存」と「はね返りの式」です。
衝突した瞬間を考えるため「摩擦力による力積」が発生せず、運動量が保存します。そして「はね返りの式」を立てれば、未知数2つ・式2本で正解が出ると見えます。
- 運動量保存則より
mV₀=mVC+mVD…(12) - はね返りの式より
V₀-0=-(VC-VD)…(13) - (12)(13)より
VC=0、VD=V₀
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(3)に関して、「物体Dに作用する力」を図で答えます。
ポイントは、問題文「矢印の向きと長さは力の向きと大きさに対応させること」です。
正確な作図を求められています。よって「重力」を基準とし、他の力線の「長さ」まで丁寧に描く必要があります。
- 物体Dにはたらく
垂直抗力をN
動摩擦力をF’とおくと
N=mgcosθ
F’=μ’N=μ’mgcosθ - 題意より、tanθ=0.3なので
cosθ=10/√109 - よって
N=10mg/√109
F’=3mg/√109
【作図のための計算】
- 上記より、力線の長さの比は
N:F’=10:3 - また、三平方の定理より
√(N²+F’²)=√(mg)²=mg
なので
垂直抗力と動摩擦力の「合力」が
重力と同じ長さになるように作図する
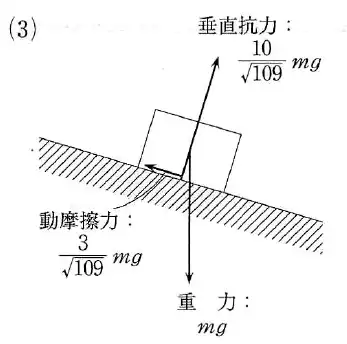
不合格者さんの一定数は不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(4)に関して、時刻t=0~t₂までの「物体CおよびDの速度の時間変化」を作図で答えます。
ポイントは「問2(1)~(3)の結果」です。
これらをグラフ上に転写する問題です。
- t=0~t₁に関して
題意より、物体Dは静止を続ける
また、問2(1)より
物体Cは初速0の等加速度直線運動をし
速度V₀に達する - t=t₁~t₂に関して
問2(2)より
Cの初速:0
Dの初速:V₀
である - 物体Cは問2(1)の運動方程式より
t=0~t₁までと同じ等加速度直線運動をする - 物体Dは問2(3)より
等速直線運動をする - よって、正解は以下の図となる
不合格者さんには少し難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問2(5)に関して、物体CとDが再び衝突するまでに「Dが移動する距離」を答えます。
- 1度目の衝突から2度目の衝突までの
時間をT₂とおくと
この間にCとDが移動した距離は等しいので
V₀T₂=1/2・gsinθ・T₂²
∴ T₂=2V₀/gsinθ - Y=V₀T₂
=2V₀²/gsinθ
=4X(∵問2(1))
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
大問2

問1(1)に関して、スイッチS₁を閉じてコンデンサーを充電した後「電極1に蓄えられた電荷Q」を答えます。
ポイントは「コンデンサの電気容量」です。
- コンデンサの電気容量をCとおくと
C=ε₀L²/d…①
となる - またコンデンサーの関係式は
Q=CV…② - ①②より
Q=ε₀L²V/d…③
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(2)に関して、コンデンサーに蓄えられた静電エネルギーUCを答えます。
- UC=1/2・QV=Q²/2C
=Q²d/2ε₀L²…④(∵①)
(これが正解です)
不合格者さんでも正解してくるレベルです。
しかし、本問に参加するには問1(1)の正解が必要です。
よって、問1(1)とセットで、合否を分ける1問より少し簡単な問題です。
問2(1)に関して、スイッチS₁を開いて電池を切り離し、電極1を距離Δxだけゆっくり上昇させた時の「静電エネルギーの増加ΔUC」を答えます。
ポイントは「変化=後-前」です。
よって、引き上げた後の静電エネルギーと問1(2)の結果を用いればよいと解ります。
- 電極1をΔxだけ上昇させた時の
電気容量をC’とおくと
C’=ε₀L²/(d+Δx) - この時の静電エネルギーUC’とおくと
UC’=Q²(d+Δx)/2ε₀L²…⑤ - ④⑤より
ΔUC=UC’-UC
=Q²Δx/2ε₀L²…⑥
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(2)に関して、電極間に働く「引力Fの大きさ」を答えます。
ポイントは「仕事とエネルギー」です。
引力と等しい大きさの外力Fを使って極板1を引き上げたので「静電エネルギーの変化=外力の仕事」となります。
- 外力がした仕事の分だけ静電エネルギーが増加したので
ΔUC=FΔx…⑦ - よって⑥⑦より
F=Q²/2ε₀L²…⑧
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問3(1)に関して、ストッパーを外した瞬間に電極2が上昇するための「Qが満たすべき条件」を答えます。
ポイントは「ストッパーを外した瞬間はバネが自然長」であることです。
つまり、極板には「引力F」と「重力」だけがはたらきます。
- ストッパーを外した瞬間に電極2にはたらく力は
x軸正方向:引力F
x軸負方向:重力mg - ゆえに
F>mg…⑨
ならば電極2が上昇する - よって求める条件は
⑧⑨より
Q>L√(2ε₀mg)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問3(2)に関して、電極2が到達する「最上点の座標xM」を答えます。
ポイントは「単振動」です。
- 極板が座標x=xにある時の加速度をaとすると
運動方程式より
ma=-mg-kx+F
∴ a=-k/m・(x+mg/k-F/k) - よって、この運動は
振動中心:x₀=1/k・(F-mg)
の単振動である - この単振動の下端はx=0なので
最上点の座標は
xM=2x₀=2/k・(Q²/2ε₀L²-mg)
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問3(3)に関して、電極間の電界のx成分Exの「時間変化を表すグラフ」を6択から答えます。
- スイッチが開いているため
コンデンサーの電荷Qは保存する - 極板間の電界の強さは
極板の電荷に依存するため
Exは一定の値を取り続ける - Exが一定の値をとり続けるグラフは
(c)のみなので、これが正解となる
合格者さんでも一定数の不正解者が出るレベルです。
よって、正解できれば他者に差をつける1問です。
問4に関して、電極2を最上点で固定し、スイッチ2を閉じ、十分時間が経つまでに抵抗R₂で消費されるエネルギーをUR₂とした時の「UC-UR₂=」を答えます。
ポイントは「エネルギーの移動」です。
| ① | コンデンサーが持っていた静電エネルギー |
| ② | バネの弾性エネルギー増加 |
| ③ | 極板の位置エネルギー増加 |
| ④ | R₂で消費されたエネルギー |
とおくと「①=②+③+④」という関係になります。求める正解は「①-④」なので「②+③」を出せば正解できるとわかります。
- スイッチS₂を閉じ、十分に時間が経つと
コンデンサーの静電エネルギーは
全て抵抗R₂で消費される - 今、R₂で消費されなかったエネルギーは
バネの弾性エネルギーの増加
極板の位置エネルギーの増加
になるので
UC-UR₂=1/2・kxM²+mgxM
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
大問3

以下、ベクトルの「→」の代わりに「*」を使って表示します。
<例>
「→v」は「v*」と表示
問1(ア)(イ)に関して、時刻tにおける物体の「x・y座標」を答えます。
ポイントは「位相を2段階に分けて考える」ことです。
立式が難しい場合は、以下の様に考えると簡単になります。
| 1 | 時間tに沿って ωtで反対向きに回る | -ωt |
| 2 | 円の頂上からスタート | +Π/2 |
- x(t)=rcos(-ωt+Π/2)=rsinωt
y(t)=rsin(-ωt+Π/2)=rcosωt
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(ウ)(エ)に関して、時刻0における物体の「速度のx成分・y成分」を答えます。
- Δtが十分に小さい時
物体の位置の変化は
v*(0)Δt…①
とみなすことができる - 物体の位置の変化を
r*を使って表すと
r*(Δt)-r*(0)
であり、題意の近似を使うと
r*(Δt)-r*(0)
=(rsin(ωΔt),rcos(ωΔt))-(0,r)
≒(rωΔt,0)-(0,r)
=(rωΔt,0)…② - ①=②なので
v*(0)=(rω,0)…③
となり
このx成分・y成分が
求める(ウ)(エ)である
vx(0)=rω
vy(0)=0
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(オ)(カ)に関して、時刻tにおける物体の「速度のx成分・y成分」を答えます。
- 物体の運動は等速円運動なので
v=|v*(0)|=rω(∵③)…④
となる - 時刻tにおける速度のx・y成分は
vx(t)=vcosωt…⑤
vy(t)=-vsinωt…⑥ - よって、⑤⑥に④を代入して
vx(t)=rωcosωt
vy(t)=-rωsinωt
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(キ)(ク)に関して、時刻0における物体の「加速度のx成分・y成分」を答えます。
- Δtが十分に小さい時
物体の速度の変化は
a*(0)Δt…⑦
とみなすことができる - 物体の速度の変化を
v*を使って表すと
v*(Δt)-v*(0)
であり、題意の近似を使うと
v*(Δt)-v*(0)
=(rωcos(ωΔt),-rωsin(ωΔt))-(rω,0)
≒(rω,-rω²Δt)-(rω,0)
=(0,-rω²Δt)…⑧ - ⑦=⑧より
a*(0)=(0,-rω²)…⑨
となり
このx成分・y成分が
求める(キ)(ク)である
ax(0)=0
ay(0)=-rω²
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(ケ)(コ)に関して、時刻tにおける物体の「加速度のx成分・y成分」を答えます。
- 物体の運動は等速円運動なので
向心方向の加速度の大きさは変わらないため
a=|a*(0)|=rω²(∵⑨)…(10)
となる - 時刻tにおける加速度のx・y成分は
ax(t)=-asinωt…(11)
ay(t)=-acosωt…(12) - よって、(11)(12)に(10)を代入して
ax(t)=-rω²sinωt
ay(t)=-rω²cosωt
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(サ)(シ)に関して、ここでシチュエーションが変わります。質量が無視できるバネと質量mの物体が大量に連結されている時「P-1番目とP+1番目の物体の回転角」を答えます。
ポイントは「回転角の進み具合」です。
大量のバネと物体の動きは、図6で与えられた1つの正弦波になっています。この正弦波の波長がλで、物体1個分の間隔がdなので、お隣り同士の回転角の差は「±2π・(d/λ)」となります。
- 正弦波の波長がλ
隣り合う物体の間隔がd
なので
隣り合う物体の回転角の差は
±2π・d/λ
となる - よって、問題文より
P番目の物体の回転角がωtなので
P-1番目:ωt+2πd/λ
P+1番目:ωt-2πd/λ
(これが正解です)
練習が行き届いた学生さんには難しくありませんが、そうでない学生さんには1問目から難しいです。
合否を分ける1問です。
問2(ス)に関して、P番目の物体の「加速度」を答えます。
ポイントは「問1の活用」です。
加速度を問わたら「運動方程式」と行く場合が多いですが、本問は問1で「加速度」を直接扱っています。よって、これを利用するのが正道と見えます。
- P番目の物体の変位
uP(t)=rsin(ωt)
とは、問1(ア)の形に等しい - よって、問1と同じプロセスにより
求める値は問1(ケ)に相当するので
aP(t)=-rω²sin(ωt)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(セ)に関して、P番目の物体が「左右のバネから受ける合力」を答えます。
ポイントは「バネの伸び・縮み」です。
P番目の物体はバネが伸び・縮みした分だけ力を受けますが、その伸び・縮みは「物体P-1、P、P+1の変位の差」で表すことができます。
- P番目の物体の
左側の伸びをΔxL(t)とおくと
ΔxL(t)=uP(t)-uP-1(t)
=rsinωt-rsin(ωt+2πd/λ)…(13) - 右側の伸びをΔxR(t)とおくと
ΔxR(t)=uP+1(t)-P(t)
=rsin(ωt-2πd/λ)-rsinωt…(14) - よって、P番目の物体が
バネから受ける合力FP(t)は
FP(t)=(14)・k-(13)・k
=(計算略・問題文の和積の公式を使う)
=-2k(1-cos(2πd/λ))×rsin(ωt)…(15)
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(ソ)に関して、P番目の物体の運動方程式を立て「ωとλの関係式」を答えます。
ポイントは「前問(ス)(セ)」です。
(ス)が加速度を求める問題で、(セ)が合力を求める問題でした。よって、この2つを使えば運動方程式を組めます。
- (ス)で求めた加速度
(セ)で求めた合力より
運動方程式を立てると
m{-rω²sin(ωt)}=-2k(1-cos(2πd/λ))・rsin(ωt)
∴ ω²=2k/m・(1-cos2πd/λ)
(これが正解です)
本問に参加するには(ス)(セ)の正解が必要です。
よって、(ス)(セ)とセットで、合否を分ける1問です。
九州大学の物理2008年・平成20年度
大問1
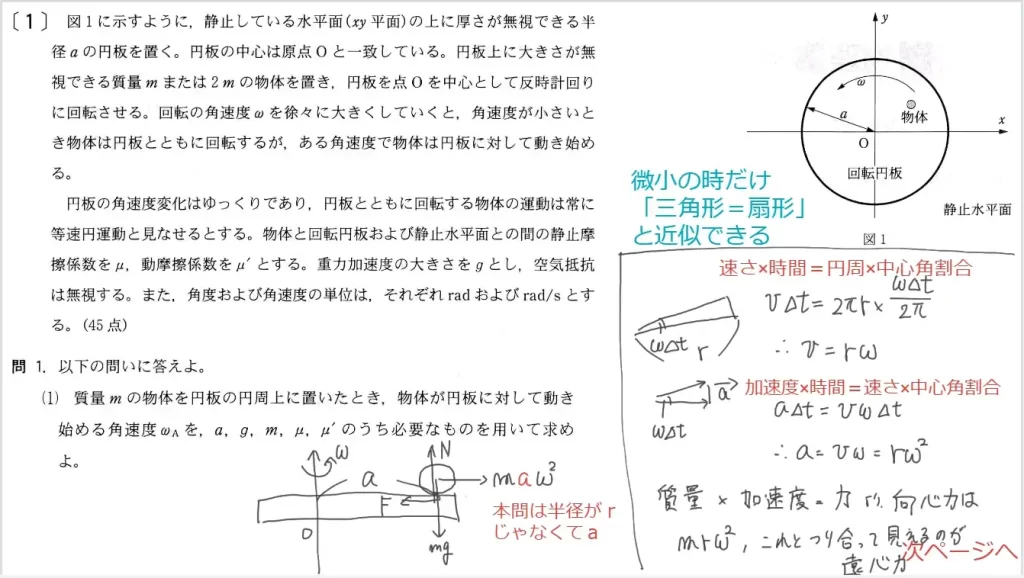
問1(1)に関して、質量mの物体を円盤の演習場に置いた時「物体が円盤に対して動き始める角速度ωA」を答えます。
- 水平方向と鉛直方向の力のつり合いより
maω²=F…①
N=mg…② - 物体が動かない条件は
F≦μN…③ - ③に①②を代入して
maω²≦μmg
∴ ω≦√(μg/a) - よって、物体が動き始める角度は
ωA=√(μg/a)…④
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)に関して、質量2mの物体を置いた時、物体が円盤に対して「動き始める角速度ω₁」を答えます。
ポイントは「問1(1)の活用」です。
問1(1)の過程で「m→2m」とすれば、本問の正解となります。
- ④において
mを2mに置き換えると
ω₁=ωA - よって
ω₁/ωA=1(倍)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(3)に関して、質量mの物体を、点Oからの距離がa/2となるように置いた時、物体が円盤上で「動き始める角速度ω₂がωAの何倍になるか」を答えます。
ポイントは「問1(1)の活用」です。
問1(1)の過程で「a→a/2」とすれば正解できます。
- ④において
aをa/2に置き換えると
ω₂=√(2μg/a)
=√2・ωA - よって
ω₂/ωA=√2(倍)
(これが正解です)
問1(2)と同様です。
全ての受験生さんが正解したい問題です。
問2(1)に関して、ここでシチュエーションが変わります。物体が円盤から離れる瞬間に、物体と点Oを結ぶ線分が「x軸となす角度θ」を答えます。
ポイントは「直角三角形」です。
板から離れる瞬間、物体の速度方向は「円盤の接線方向」です。よって、角θはsinを使って表すことができます。
- 物体が円盤から離れる点をQとおく
- 物体は点Qから
円周の接線方向へ発射されるため
∠PQO=π/2
であり
∠OPQ=θ
となる - よって
sinθ=QO/OP
=1/√2
より
θ=π/4
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、物体が点Pへ到達するために必要な「ωAに関する条件」を答えます。
ポイントは「点Pにおける速度」です。
物体は点Pに到達するまで床から動摩擦力を受け、減速しながら進みます。逆に言えば「点Pにおける速度が0以上」なら、物体は点Pに到達できるということです。
- 物体が水平面上を移動する時
加速度をαとすると運動方程式は
水平方向:mα=-μ’N…⑤
鉛直方向:0=mg-N…⑥ - ⑤⑥より
α=-μ’g…⑦ - 点P・Qにおける物体の速度を
vP・vQとおくと
vP²-vQ²=2αa…⑧ - 物体が点Pに到達する条件は
vP≧0なので
⑧より
vP=√(vQ²-2μ’ga)≧0
∴vQ≧√(2μ’ga)…⑨ - また
vQ=aωA…(10)
なので
⑨(10)より
ωA≧√(2μ’g/a)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(3)に関して、物体が円盤から離れた後、点Pで「壁と衝突するまでの時間t」を答えます。
ポイントは「等加速度直線運動」です。
三角形OPQは直角二等辺三角形と判っているので、PQの長さはaとなります。よって、等加速度直線運動の式が使えます。
- 問1(1)のθ=π/4
∠PQO=π/2
OP=√2・a
より
PQ=a
となる - ⑦より
物体はQP間を等加速度直線運動するので
a=aωA・t+1/2・(-μ’g)・t²
上記をtの二次方程式とみなすと
解の公式より
∴ t=[aωA±√{(aωA)²-2μ’ga}]/μ’g - 題意より
物体と壁は初めて衝突するので
t=[aωA-√{(aωA)²-2μ’ga}]/μ’g
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(4)に関して、点Pで衝突する直前の「物体の速さv₁」を答えます。
ポイントは「等加速度直線運動」です。
問2(3)のtを「速さの式」に代入しても正解は出ますが、計算過程が大変なので以下の解き方を使います。
- 物体はPQ間を等加速度直線運動するので
v₁²-(aωA)²=2(-μ’g)a
∴ v₁=√{(aωA)²-2μ’ga}
(これが正解です)
問2(3)と同等の難易度です。
よって、合否を分ける1問より少し簡単な問題です。
問3(1)に関して、物体が壁に衝突した直後の「速度のx成分・y成分」を答えます。
以降、ベクトルの「→」を「*」で表します。
例:「→a」は「a*」と表示
- 題意より、壁の表面はなめらかなので
衝突前後で物体の
速度のx成分は変化しない
∴ v₂x=v₁x - また、問2(1)より
物体は壁に対し
角度π/4で衝突するので
v₂x=v₁x
=-|v₁*|sinπ/4
=-v₁/√2
(これが正解です) - 続いて、速度のy成分に関して
はね返りの式より
(v₂y-0)=-e(v₁y-0)
∴ v₂y=-ev₁y - 物体は壁に対し
角度π/4で衝突するので
v₂y=-ev₁y
=-e|v₁*|cosπ/4
=-ev₁/√2
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3(2)に関して、点Pで壁に衝突した物体が「静止するまでに運動した距離l」を答えます。
- 衝突後の物体の速さv₂は
v₂=√(v₂x²+v₂y²)
=√{(1+e²)/2}・v₁ - 衝突後の物体は
⑤⑥の等加速度直線運動をするので
0²-v₂²=2(-μ’g)l
∴ l={(1+e²)v₁²}/4μ’g
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
大問2

問1に関して、t=0~π/ωの間で「a・bのどちらが高電位か」を答えます。
ポイントは「レンツの法則」です。
【レンツの法則】
回路を貫く磁束の変化を妨げる方向に誘導起電力が発生する
- 時刻t=0~π/ωにおいて
図3の回路を貫く磁束は増加する - よって、レンツの法則より
磁束の増加を妨げる方向へ
誘導起電力が発生するので
「aが高電位」となる
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、時刻tにおける領域WXYZを貫く磁束Φ(t)を答えます。
ポイントは「面積」です。
軸の回転により、磁場の貫く面積が小さくなっていきますが、その値は三角関数を使って「d²cosωt」と表現できます。磁束密度Bが与えられているので、面積がわかれば正解できます。
- t=0における
領域WXYZの面積は
d²である - ゆえに、題意の時刻において
磁場が貫く領域の面積は
d²cosωt
となる - よって
Φ(t)=Bd²cosωt…①
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、微小時間Δtにおける磁束の変化を「ΔΦ=k₁Δtと書いた時のk₁」を答えます。
ポイントは「変化=後-前」です。
- 時刻t+Δtにおける磁束は①より
Φ(t+Δt)=Bd²cosω(t+Δt)
=Bd²(cosωt・cosωΔt-sinωt・sinωΔt)
≒Bd²(cosωt-ωtsinωt)…② - よって、磁束の変化は
ΔΦ=Φ(t+Δt)-Φ(t)
=②-①
=-ωBd²sinωt・Δt…③
より
k₁=-ωBd²sinωt
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4に関して、時刻tにおいてab間に発生する「誘導起電力V(t)」を答えます。
ポイントは「ファラデーの電磁誘導の法則」です。
誘導起電力は「単位時間あたりの磁束の変化」となります。それは問3で求めています。
- 電磁誘導の法則より
誘導起電力の大きさは
|V(t)|=|ΔΦ/Δt|
=ωBd²sinωt(∵③) - 今、題意の時刻においては
aが高電位なので
V(t)=ωBd²sinωt…④
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問5に関して、時刻tにおいて抵抗に流れる「電流IR(t)」を答えます。
ポイントは「オームの法則」です。
問4で電圧V(t)を求めており、抵抗の大きさはRなので、オームの法則を使えば正解できます。
- IR(t)=V(t)/R
=(ωBd²sinωt)/R…⑤
(これが正解です)
オームの法則を使うだけなので、不合格者さんでも正解してきます。
しかし、本問に参加するためには問3の正解が必要です。
よって、問3とセットで、合否を分ける1問より少し簡単な問題です。
問6に関して、時刻tにおいてコンデンサーに蓄えられる電気量をQ(t)とした時、その変化量「ΔQ=k₂Δtにおけるk₂」を答えます。
ポイントは「変化=後-前」です。
問3と同じプロセスを電気量Qで用います。
- コンデンサーの式と④より
Q(t)=CV(t)=ωCBd²sinωt - 時刻t+Δtにおける電気量は
Q(t+Δt)=ωCBd²sinω(t+Δt)
=ωCBd²(sinωt・cosωΔt+cosωt・sinωΔt)
≒ωCBd²(sinωt+cosωt・ωΔt) - ゆえに変化量は
ΔQ=Q(t+Δt)-Q(t)
=ω²CBd²cosωt・Δt…⑥ - よって
k₂=ω²CBd²cosωt
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問7に関して、時刻tにおいてコンデンサーに流れる「電流Ic(t)」を答えます。
- ⑥より
Ic(t)=ΔQ/Δt
=ω²CBd²cosωt…⑦
(これが正解です)
不合格者さんでも正解してくるレベルです。
しかし、本問に参加するには問6の正解が必要です。
よって、問6とセットで、合否を分ける1問より少し簡単な問題です。
問8に関して、時刻t=0~2π/ωにおける「Ic(t)のグラフ」を描きます。
ポイントは「問7の利用」です。
答えるべきIc(t)は問7で導出しており、tの関数となっています。よって、以下の図が正解となります。
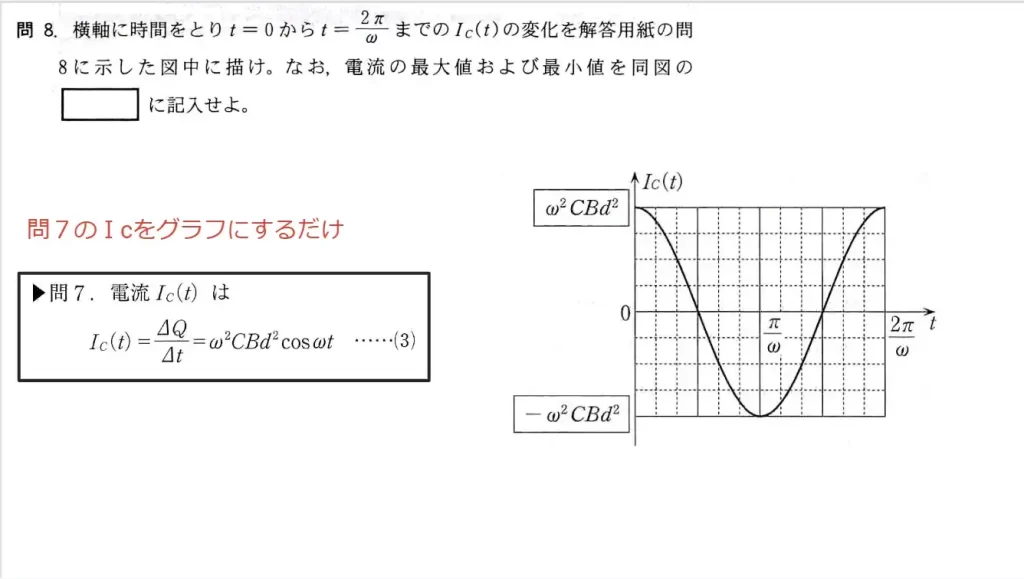
不合格者さんでも正解してくるレベルですが、本問に参加するには問7の正解が必要です。
よって、問7とセットで、合否を分ける1問より少し簡単な問題です。
問9に関して、IR(t)に対する「Ic(t)の位相」を答えます。
ポイントは「問5と問7の活用」です。
IR(t)は問5で、Ic(t)は問7で求めています。2つの位相の差を調べるには、三角関数を揃えればよいです。
- ⑦より
Ic(t)=ω²CBd²cosωt
=ω²CBd²sin(ωt+π/2)…⑦’ - よって
⑤と⑦’を比較すると
Ic(t)はIR(t)に対し
位相がπ/2進んでいる。
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
大問3
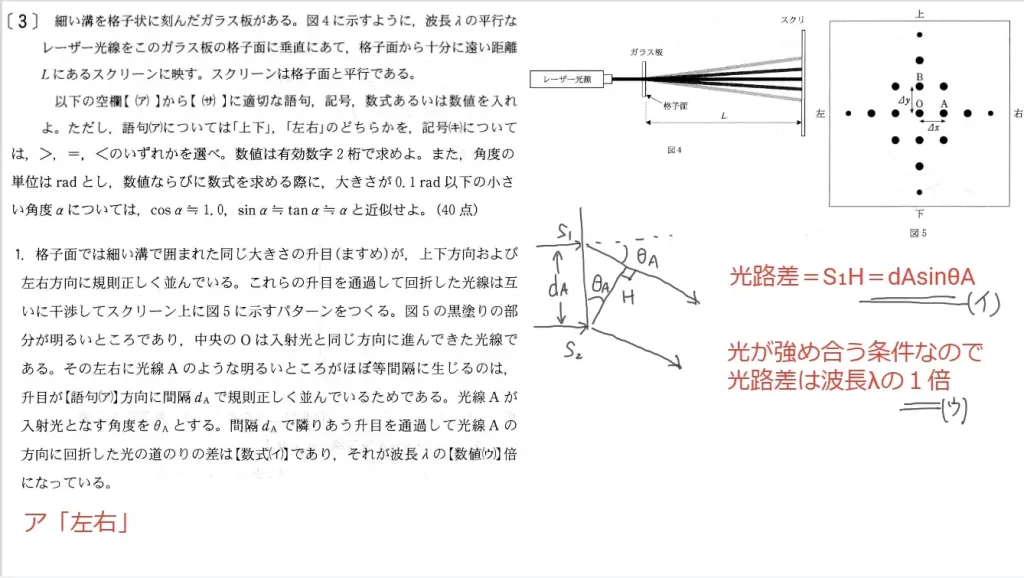
問アに関して、図5に示されるように、点Oの左右に光線Aのような明るい部分が等間隔に生じる理由を答えます。
- 点Oの左右に光線Aのような明るいところが
ほぼ等間隔に生じるのは、
升目が「ア:左右」方向
に規則正しくならんでいるからである
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問イ・ウに関して、隣り合う升目からAへ向けて回折した「光の道のりの差」と「その差が波長の何倍か」を答えます。
ポイントは「三角関数」です。
屈折後の角度θAが与えられているため、光路差はsinθAを使って表現できます。
- 題意より
隣り合う升目の間隔はdAであり
光線Aが入射光と成す描くはθAなので
光路差=dAsinθA
(これがイの正解です) - また、光線Aは光が強め合う関係になっているので
光路差は波長λの「ウ:1倍」となる
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問エに関して、光線Aが「入射光と成す角θA」を答えます。
ポイントは「問題文で与えられた数値」です。
問題文では「格子面からスクリーンまでの距離L」と「光線Oと光線Aの間隔Δx」が与えられています。そして、格子面から点Aへの角度がθAなので、三角関数で表現できる・・・という流れです。
- 与えられた条件より
tanθA=Δx/L
=32/2000
=1.6×10⁻²(rad) - 題意より、上記は0.1rad以下なので近似を使える
よって
θ≒tanθA=1.6×10⁻²(rad)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問オ・カに関して、「格子の間隔dA」を答えます。
ポイントは「題意の近似:sinα≒tanα」です。
- 隣り合う格子からAへ向かう光の光路差は
(イ)よりdAsinθA - その光路差は(ウ)より
波長の1倍の長さなので
dAsinθA=λ…① - また(エ)より
tanθA=Δx/L…② - ここで題意より
sinθA≒tanθAなので
①②を代入して
λ/dA=Δx/L
∴ dA=Lλ/Δx…③
(これが正解です) - また
tanθA≒sinθA=λ/dA…④
より
dA=λ/tanθA
=0.53/1.6×10⁻²
=33.1
≒33(μm)
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問キに関して、格子の縦方向の間隔を求め、横方向の間隔(dA)と比較します。
ポイントは「問オの活用」です。
先程の問題でdAの長さ(dA=Lλ/Δx)を求めました。Lとλは問題文で与えられた条件なので一定の値です。よって「Δx→Δy」とすれば「dA→dB」となります。
- 格子からスクリーンの距離Lと
波長λは光線A・Bに関して一定なので
③より
dB=Lλ/Δy…⑤ - 題意より
Δy>Δxなので③⑤を比較して
dB<dA
(これが正解です)
dA=Lλ/ΔxをdBに転用できる事に気づけば、それほど難しくありません。
しかし、本問に参加するには問オの正解が必要なので、問オとセットで合否を分ける1問です。
問ク・ケに関して、ここでシチュエーションが変わります。格子面とスクリーンの間に凸レンズを起き、スクリーンに鮮明な格子の拡大像が現れた時の「レンズの焦点距離」を答えます。
ポイントは「レンズの公式」です。
図6は複雑ですが、下段で「a」と「b」の長さが与えられています。よって、レンズの公式が使えばよいと解ります。
- レンズの式より
1/a+1/b=1/f…⑥ - 今、題意より
a=50
b=1950
なので⑥より
f=48.75≒49(mm)
(これが正解です) - また、倍率Mは
M=|b/a|=39(倍)
(これが正解です)
急にレンズが出てきて大変ですが、レンズの式を使うだけです。
不合格者さんでも正解してくるので、全ての受験生さんが正解したい問題です。
問コに関して、図6に示された「Dの長さ」を答えます。
- レンズの中心と点F₀・点FAが作る直角三角形より
tanθA=D/f…⑦ - ④⑦より
λ/dA=D/f
∴ D=fλ/dA
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
しかし、本問に参加するには問カの正解が必要なので、問カとセットで合否を分ける1問です。
問サに関して、縞の「隣り合う明線の間隔ΔX」を答えます。
- 点F₀と点FAを通った光が
スクリーンの同じ場所に
明線を作る場合を考える - 光線が入射角となす角をθ’とおくと
光路差=Dsinθ’
≒Dtanθ’
=DX/l - 自然数mを用いると
m番目の明線の条件は
DX/l=mλ…⑧ - また、m+1番目の明線の条件は
D(X+ΔX)/l=(m+1)λ…⑨ - ⑧⑨より
ΔX=lλ/D
(これが正解です)
合格者さんでも一定数の不正解が出るレベルです。
よって、合否を分ける1問より少し難しい問題です。
九州大学の物理2007年・平成19年度
大問1

以下「単位」を省略して書きます。
回答の際は単位を付けてください。
問1(1)に関して、バネに繋がれた物体Aに物体Bを押し付けてバネを縮め、手を放した時、物体AとBが「離れるまでの時間T」と「物体Bの速度v₀」を答えます。
ポイントは「単振動」です。
物体Aはバネに繋がれて単振動するので、振動中心を超えると進行方向と反対向きに加速度がかかり、Bと離れます。
- 題意の状況において
物体A・B間の抗力をR
加速度をβ₀
とおく - バネの自然長の位置を原点として
右向きにx軸をとり
物体Aの左端がx=xにある時の
物体A・Bの水平方向の運動方程式は
mβ₀=-kx-R…①
mβ₀=R…② - ②-①より
R=-1/2・kx…③ - 物体A・Bが離れる条件は
R=0
なので、それは③より
x=0
でおこる - ①③より
β₀=-k/2m・x
ゆえにAは
振動中心:x=0
角振動数:√(k/2m)
の単指導をするので
Bと離れるのは、周期T₀として
T=1/4・T₀
=π√(m/2k)
(これが正解です) - また、力学的エネルギー保存則より
1/2・kL²=1/2・2m・v₀²
∴ v₀=L√(k/2m)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(2)に関して、物体Aの単振動の「振幅D」と「角振動数ω」を答えます。
ポイントは「力学的エネルギー保存則」です。
Bと離れた瞬間のAの速度はv₀であり、この運動エネルギーがバネの弾性エネルギーとなるので、振幅を知ることができます。
- 物体Aに関する力学的エネルギー保存則より
1/2・mv₀²=1/2・kD²
∴ D=v₀√(m/k)
=L/√2
(これが正解です) - また、物体Aの位置x=xにおける運動方程式は
加速度をα₀として
mα₀=-kx
∴ α₀=-k/m・x - よって、角振動数は
ω=√(k/m)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(1)に関して、ここでシチュエーションが変わります。物体Bが台車の上を滑る時、時刻tにおける「物体Bの速度v」および「台車の速度V」を答えます。
ポイントは「運動方程式」です。
時刻tにおける速度を求められているので「速度=初速+加速度×t」となります。
- 物体B・台車の水平方向の加速度を
β・aとおき
物体Bが台車から受ける垂直抗力をN
台車が地面から受ける垂直抗力をN台とおくと
両者の水平・鉛直方向の運動方程式より
mβ=-μ’N…④
0=N-mg…⑤
Ma=μ’N…⑥
0=N台-N-Mg…⑦ - ④⑤より
β=-μ’g…④’
⑤⑥⑦より
a=mμ’g/M…⑥’ - 等加速度直線運動の式より
v=v₀+βt=v₀-μ’gt…⑧
(これが正解です)
V=0+at=mμ’gt/M…⑨
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、時刻tまでに物体Bが「台車の上面を滑った距離d」を答えます。
- 時刻tにおいて、物体Bおよび台車が
段差から距離d₁およびD₁の位置にあると仮定すると
等加速度直線運動の式より
d₁=v₀t+1/2・βt²
=v₀t-1/2・μ’gt²
D₁=0+1/2・at²
=1/2・mμ’gt²/M - この差が求める距離dとなるので
d=d₁-D₁
=v₀t-1/2・(M+m)μ’gt²/M
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(3)に関して、物体Bと台車の運動が「一体となった時刻t₁」および、その時の「速度V₁」を答えます。
- ⑧⑨より
v₀-μ’gt₁=mμ’gt₁/M
∴ t₁=Mv₀/μ’g(M+m)…(10)
(これが正解です) - また⑨(10)より
V₁=mμ’gt₁/M
=mv₀/(M+m)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問3に関して、一体となった物体Bと台車が向かい側のバネに衝突し、物体Bが台車の上を滑らずに向きを変えた時の「バネ定数Kの範囲」を答えます。
ポイントは「滑らない条件」です。
問題が「Kの範囲を示せ」ということで、何かしら「不等式」を立てる必要があります。本問の条件で不等式を立てられそうなのは「Bと台車間の摩擦力」となります。
- バネの自然長の位置を原点とし
右向きにX軸をとる - 物体および台車の加速度をβ’とおき
両者の間にはたらく摩擦力をFとおくと
水平・鉛直方向の運動方程式は
mβ’=-F…(11)
0=N-mg…(12)
Mβ’=F-KX…(13)
0=N台-N-Mg…(14) - また、物体Bが滑らない条件は
F≦μN…(15)
である - (11)×M-(13)×mより
F=mKX/(M+m)…(16) - (16)において
摩擦力が最大となるXを
X=X₁
とおくと、力学的エネルギー保存則より
1/2・(M+m)V₁²=1/2・KX₁²
∴ X₁=V₁√{(M+m)/K}…(17) - よって、物体Bが滑らない条件は
(15)(16)より
mKX₁/(M+m)≦μmg
(17)を代入して
K≦(M+m)(μg/V₁)²
(これが正解です)
合格者さんでも一定数が不正解になるレベルです。
よって、合否を分ける1問より少し難しい問題です。
問4(1)に関して、バネで跳ね返った2物体が今度は反対の段差に衝突します。この衝突直後の「物体Bの速度v₁’」と「台車の速度V₁’」を答えます。
ポイントは「台車が段差に衝突した瞬間の、物体Bにはたらく外力」です。
- 力学的エネルギー保存則より
バネで跳ね返って左向きに進む台車と物体Bの速さは
V₁となる - 今、台車がQQ’の段差に衝突しても
その瞬間に物体Bが
衝突による外力を受けることはないので
v₁’=-V₁
(これが正解です) - また、台車に関して
はね返りの式より
V₁’-0=-e(-V₁-0)
∴ V₁’=eV₁
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問4(2)に関して、物体Bと台車が同時に静止した時の「反発係数e」を答えます。
ポイントは「問2(1)の活用」です。
本問において、摩擦力は内力となるため(外力による力積が加わらないため)運動量保存則により「m(-V₁)+MeV₁=0」で、正解はすぐ出ます。
しかし、せっかく問2を解いたプロセスがあるので、多少手間が増えても運動方程式から慎重に行く方が良いと思います。
- 物体B・台車の加速度をβ’’・a’’とおくと
運動方程式より
mβ’’=μ’N…(A)
0=N-mg…(B)
Ma’’=-μ’N…(C)
0=N台-N-Mg…(D) - (A)(B)より
β’’=μ’g…(E)
(B)(C)より
a’’=-mμ’g/M…(F) - 段差で衝突してから
静止するまでの時間をt₂とおくと
0=-V₁+β’’t₂…(G)
0=eV₁+a’’t₂…(H) - (E)~(H)より
e=m/M
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
大問2
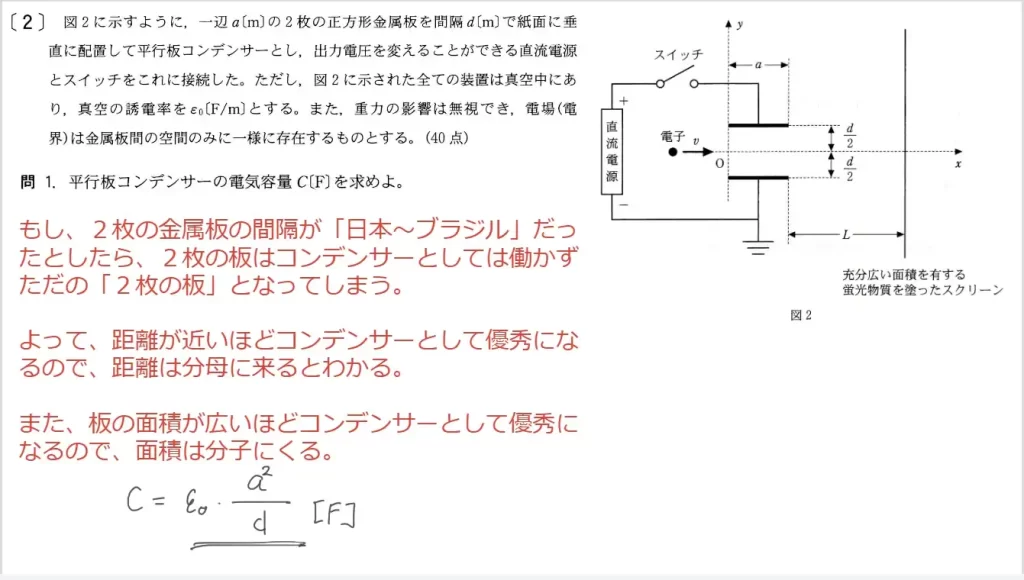
以下「単位」を省略して書きます。
回答の際は単位を付けてください。
問1に関して、平行板コンデンサーの「電気容量」を答えます。
- 2枚の金属板の
面積:a²
距離:d - よって
C=ε₀a²/d…①
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、スイッチを閉じた状態における、コンデンサーに蓄えられた「電気量」と「静電エネルギー」を答えます。
- 題意より電気量Qは
Q=CU₁
=ε₀a²U₁/d(∵①)
(これが正解です) - また、静電エネルギーは
W₁=1/2・CU₁²
=ε₀a²U₁²/2d(∵①)
(これが正解です)
問1同様、基礎知識なので不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問3に関して、コンデンサー内を通過する「電子が受ける力」を答えます。また、電子がコンデンサーの金属板に当たるようになった時の「コンデンサーの電位差」を答えます。
- 電位差がU₂の時の
極板間に発生する電場の強さをE₂とおくと
E₂=U₂/d - よって、電子が受ける力の大きさは
F=eE₂
=eU₂/d
(これが正解です) - また、電子のy軸方向の加速度をαとおくと
運動方程式より
mα=eU₂/d
∴ α=eU₂/md…② - 電子が点Oから上側極板の右端に
到達するまでの時間をt₃とおくと
x・y方向の移動距離は
a=vt₃…③
d/2=1/2・αt₃²…④ - ②~④より
U₃=mv²d²/ea²…⑤
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4に関して、スイッチを開いてしばらく待ち、電子による輝点がスクリーンに現れるようになるまでの「時間T」と「輝点のy座標」を答えます。
ポイントは「コンデンサーの電気量の変化」です。
- T₀秒間にコンデンサーに投入された電子の数
- 電位の変化(U₄→U₃)によるコンデンサーの式
という2種類の方法で表すことができるため「=」でつなげば方程式を作れます。
- 電位差U₄の状態からスイッチを開き
電子が極板に捉えられ
電位差がU₃より小さくなると
電子は極板を越えてスクリーンへ向かう - 上記にかかる時間をT₀とおくと
この間に入射した電子の電気量は
ΔQ=-eNT₀…⑥
となる - また、電位差U₃・U₄における
極板の電気量をQ₃・Q₄とおくと
ΔQ=Q₃-Q₄
=C(U₃-U₄)…⑦ - よって①と⑤~⑦より
-eNT₀=ε₀a²/d・(mv²d²/ea²-U₄)
∴ T₀=ε₀a²/eNd・(U₄-mv²d²/ea²) - 電子が極板の右端から
スクリーンまでにかかる時間は
L/v
なので
T=T₀+L/v
=ε₀a²/eNd・(U₄-mv²d²/ea²)+L/v
(これが正解です) - 極板上側の右端を通過する時の
電子の速度のy方向成分は
y方向の加速度α’として
vy=α’t₃
=eU₃a/mdv
=vd/a - よって、極板上川のy座標はd/2なので
y₁=d/2+vd/a・L/v
=d(1/2+L/a)
(これが正解です)
合格者さんでも一定数の不正解が出るレベルです。
よって、合否を分ける1問より少し難しい問題です。
問5に関して、スイッチを閉じてコンデンサーの電位差をU₅とした時、電子がコンデンサー内を通過する間に「電場から得るエネルギー」を答えます。
- 問3と同様のプロセスを用いると
電子が極板から飛び出す瞬間の
速度のx・y成分は
x:v…⑧
y:eU₅a/mdv…⑨
となる - 求める値W₂は
コンデンサーを通過する前後の
運動エネルギーの変化に等しいので
W²=1/2・m(⑧²+⑨²)-1/2・mv²
=1/2m・(eU₅a/dv)²
(これが正解です)
問4に比べると簡単ですが、問4のプロセスの一部が必要な問題です。
よって、問4とセットで、合否を分ける1問より少し難しい問題です。
大問3
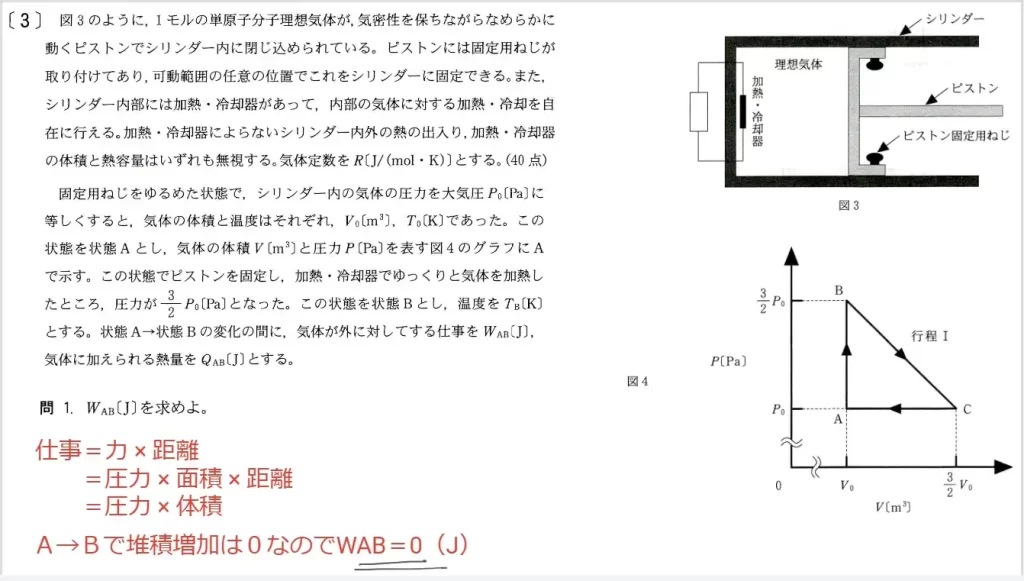
以下「単位」を省略して書きます。
回答の際は単位を付けてください。
問1に関して、状態A→Bの変化において「気体が外部へする仕事WAB」を答えます。
- 仕事=力×距離
=(圧力×面積)×距離
=圧力×(面積×距離)
=圧力×体積 - 今、A→Bの変化において
体積変化は0なので
WAB=0…①
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2に関して、状態A→Bの変化において「気体に加えられる熱量QAB」を答えます。
ポイントは「状態方程式」です。
「気体に加えられる熱量」を求めるということで、熱力学第一法則を使うことが見えます。そのためには「内部エネルギーの変化ΔUAB」が必要で、状態Bの温度がわかればよい・・・という流れです。
- 状態Aに関する状態方程式より
P₀V₀=RT₀…②
状態Bに関する状態方程式より
3/2・P₀V₀=RTB…③ - ②③より
TB=3/2・T₀ - よって、熱力学第一法則より
QAB=ΔUAB+WAB
=3/2・R(3/2・T₀-T₀)+0
=3/4・RT₀
(これが正解です)
不合格者さんの一定数が不正解になる程度です。
よって、合否を分ける1問より少し簡単な問題です。
問3に関して、状態B→Cの変化において「気体が外部へする仕事WBC」および「気体に加えられる熱量QBC」を答えます。
ポイントは「図4のPVグラフ」です。
気体が外部へする仕事は「PVグラフの面積」で求めることができます。
- 図4のPVグラフより
気体が外部にする仕事WBCは
線分BCとV軸による
台形の面積に等しいので
WBC=1/2・(3/2・P₀+P₀)(3/2・V₀-V₀)
=5/8・RT₀ - また、条件より
状態B・Cの温度が等しいことから
内部エネルギーの変化は0
となる - よって、熱力学第一法則より
QBC=0+5/8・RT₀
=5/8・RT₀
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問4に関して、状態C→Aの変化において「気体がされる仕事WCA」と「気体から奪われる熱量QCA」を答えます。
- 気体がされる仕事WCAは
図4のPVグラフにおける
線分CAとV軸による
長方形の面積なので
WCA=P₀(3/2・V₀-V₀)
=1/2・RT₀
(これが正解です) - この変化における
内部エネルギーの変化は
ΔUCA=3/2・R(3/2・T₀-T₀)
=3/4・RT₀ - よって、熱力学第一法則より
QCA=ΔUCA+WCA
=5/4・RT₀
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問5に関して、サイクルⅠにおける「熱効率e₁」を答えます。
ポイントは「熱効率の定義」です。
以下の式に問1~4の結論を代入すると正解できます。
【熱効率】
外部にした仕事 ÷ 吸収した熱
- e₁=(WAB+WBC-WCA)/(QAB+QBC)
=1/11
(これが正解です)
問1~4のまとめとなる1問です。
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問6に関して、ここでシチュエーションが変わります。先程までの「サイクルⅠ」に加え「サイクルⅡ」が登場します。サイクルⅡにおける「熱効率e₂」を答えます。
ポイントは「情報の整理」です。
何をすればよいのかイマイチ見えにくい問題なので、情報を整理して「目標」を明確にしましょう。
| サイクルⅠ | サイクルⅡ | |
|---|---|---|
| A→B | QAB WAB | QAB WAB |
| B→C | QBC WBC | QBC’ WBC’ |
| C→A | QCA WCA | OCA WCA |
| 正味の仕事 | WⅠ =0+WBC-WCA | WⅡ =0+WBC’-WCA |
- QBC=WBC=WⅠ+WCA
∴ WCA=QBC-WⅠ - QBC’=WBC’
=WⅡ+WCA
=WⅡ+QBC-WⅠ - よって
eⅡ=WⅡ/(QAB+QBC’)
=WⅡ/(QAB+QBC-WⅠ+WⅡ)
(これが正解です)
不合格者さんには厳しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問7に関して、熱効率eⅠとeⅡの「大小関係」を答えます。
- eⅠ-eⅡ
=WⅠ/(QAB+QBC)-WⅡ/(QAB+QBC-WⅠ+WⅡ)
=(QAB+QBC-WⅠ)(WⅠ-WⅡ)/(QAB+QBC)(QAB+QBC-WⅠ+WⅡ)…④ - ④式の分母は
eⅠの分母(>0)とeⅡの分母(>0)の
掛け算なので正の値となる - またWⅠ-WⅡは題意より
行程Ⅰと行程Ⅱで気体が外部へする仕事が
行程Ⅰ>行程Ⅱとなるため
WⅠ-WⅡも正の値となる - QAB+QBC-WⅠ
=QAB+(WⅠ+WCA)-WⅠ
=QAB+WCA
=3/4・RT₀+1/2・RT₀
=5/4・RT₀>0 - よって、以上より
④>0となるので
eⅠ>eⅡ
(これが正解です)
合格者さんでも一定数の不正解者が出るレベルです。
よって、合否を分ける1問より少し難しい問題です。
九州大学の物理2006年・平成18年度
大問1
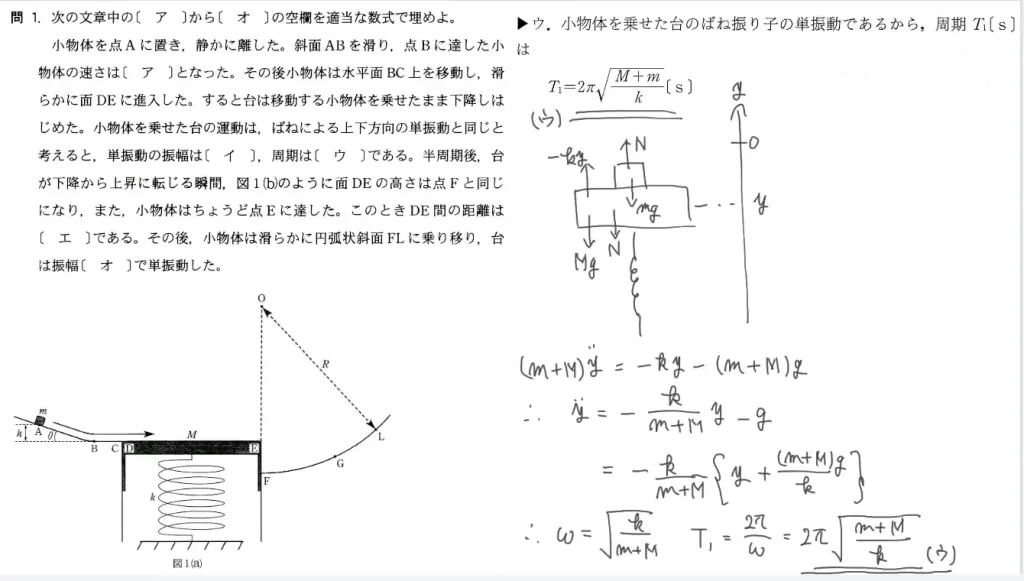
以下「単位」を省略して書きます。
回答の際は単位を付けてください。
問1(ア)に関して、斜面を滑り落ち点Bに達した「小物体の速さ」を答えます。
ポイントは「力学的エネルギー保存則」です。
斜面の摩擦は無視できるため、重力による位置エネルギーが運動エネルギーに変わります。
- 点Bにおける小物体の速さをvBとおくと
力学的エネルギー保存則より
1/2・mvB²=mgh
vB=√(2gh)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(イ)(ウ)に関して、小物体が台に乗った時の、単振動の「振幅」と「周期」を答えます。
ポイントは「単振動の上端」です。
小物体と台を一体とみなして鉛直方向の運動方程式を立てると、この運動が単振動であるとわかり「振動中心」が求まります。振幅を求めるためには運動の「上端」か「下端」がわかればよいですが、本問では「上端」で台にかかる重力と弾性力がつり合っているため立式できます。
- 小物体と台を一体と考え
鉛直方向にy軸をとって
バネの自然長の位置をy=0とおくと
一体のy軸方向の運動方程式は
加速度βとして
(m+M)β=-ky-(m+M)g
∴ β=-k/(m+M)・{y+(m+M)g/k} - 上式より、この運動は
振動中心:y₀=-(m+M)g/k…①
角振動数:ω=√{k/(m+M)}…②
の単振動である - また、この単振動の上端y=y₁は
台とバネがつり合う位置なので
-ky₁-Mg=0
∴ y₁=-Mg/k…③ - よって振幅Aは
A=③-①
=mg/k…④
(これが正解です) - また、周期をT₁とおくと
T₁=2π/ω
=2π√{(m+M)/k}(∵②)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(エ)に関して、台上の「DE間の距離」を答えます。
- DE間の距離をlとおく
- 小物体の速さはvBであり
DE間の移動時間はT₁/2なので
l=vB・T₁/2
=√(2gh)×2π√{(M+m)/k}×1/2
=π√{2(M+m)gh/k}
(これが正解です)
速さvB、時間T₁/2は解りやすいので、不合格者さんでも正解してきます。
しかし、本問に参加するためには、問1(ウ)の正解が必要です。
よって、問1(ウ)とセットで、合否を分ける1問より少し簡単な問題です。
問1(オ)に関して、小物体が台から降りた後、台の「単振動の振幅」を答えます。
ポイントは「点Fのy座標」です。
台のy方向の運動方程式を書けば「振動中心」は求まります。この単振動の下端は点Fなので、点Fのy座標を求めれば振幅が出て正解となります。
- 小物体がFに移った後の
台のy軸方向加速度をβ’とおくと
運動方程式は
Mβ’=-ky-Mg
∴ β’=-k/M・(y+Mg/k) - よって、台は
振動中心:y₀’=-Mg/k…⑤
角振動数:ω’=√(k/M)…⑥
の単振動をする - 点Fのy座標は
①-④より
-(2m+M)g/k…⑦ - よって、求める振幅をA’とおくと
A’=⑤-⑦
=2mg/k
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(1)に関して、台を抜けた小物体の運動を使って「点Gが点Fよりどれだけ高いか」を答えます。
ポイントは「力学的エネルギー保存則」です。
斜面の摩擦は考えなくてよいので、運動エネルギーと位置エネルギーが交換されます。
- 求める高さをh’として
力学的エネルギー保存則より
1/2・mvB²=mgh’
∴ 1/2・m・2gh=mgh’
∴ h’=h
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、円弧FGの長さが半径Rに比べてかなり小さく、小物体の運動が単振り子とみなせる時の「小物体が円弧FGを往復する時間」を答えます。
ポイントは「単振り子の周期」です。
問題文の「FGを往復する時間」とは単振り子の半周期です。単振り子の周期は、円弧方向の運動方程式から角振動数を出せば求まります。
- 小物体の運動を単振り子とみなし
半径が地面鉛直となす角をθ
小物体の円弧方向の加速度をαとおくと
運動方程式より
mα=-mgsinθ
∴ α=-gsinθ…⑧ - 題意より
円弧FGが十分小さいため
sinθ≒θ…⑨
と近似できる - また、円弧FGの長さをl’とおくと
l’=2πR×θ/2π
=Rθ
∴θ=l’/R…(10) - 円弧方向にx軸をとると
⑧⑨(10)より
α≒-gθ
=g/R・x - ゆえにこの単振り子は
角振動数:ω’’=√(g/R)
周期:T₂=2π/ω’’=2π√(R/g) - 今、求める時間をt₂とおくと
t₂=T₂/2
=π√(R/g)…(11)
(これが正解です)
合格者さんでも一定数は不正解になるレベルです。
よって、合否を分ける1問より少し難しい問題です。
問2(3)に関して、小物体が点Fに戻ってきた時に再び台と同じ高さになる場合の「半径R」を答えます。
- ⑥より
台の鉛直方向の単振動の周期T₃は
T₃=2π/ω’
=2π√(M/k)…(12) - 題意より
(11)=(12)なので
R=4Mg/k
(これが正解です)
本問自体はあまり難しくありません。
しかし、本問に参加するには、問2(2)の正解が必要です。
よって、問2(2)とセットで、合否を分ける1問より少し難しい問題です。
問3(1)に関して、小物体が台をE→Dと通って点Bに戻り、摩擦を受けながら斜面ABを登った時の「停止点がB点よりどれだけ高いか」を答えます。
ポイントは「仕事とエネルギーの関係」です。
点Bにおける小物体の運動エネルギーが「摩擦力の仕事」と「重力に関する位置エネルギー」に変わります。
- 点Bを原点とし
B→A方向にx軸をとる - 小物体の
x軸方向の加速度をα’
斜面から受ける垂直抗力をNとおくと
斜面と斜面鉛直方向の運動方程式より
mα’=-mgsinθ-μ’N…(13)
0=N-mgcosθ…(14) - (13)(14)より
動摩擦力の大きさは
μ’mgcosθ - 求める高さをHとおくと
小物体が摩擦を受けながら
斜面を登った距離Lは
L=H/sinθ - よって
動摩擦力がした仕事と
小物体の運動エネルギーの関係より
μ’mgcosθ・L+mgH=1/2・mvB²
∴ μ’mgH/tanθ+mgH=mgh
∴H=tanθ/(tanθ+μ’)・h
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくるレベルです。
よって、合否を分ける1問です。
問3(2)に関して、小物体が斜面で停止した後「滑り落ちないための静止摩擦係数μの条件」を答えます。
- 静止摩擦力をFとし
(13)(14)を
小物体が静止した場合に書き換えると
0=F-mgsinθ
0=N-mgcosθ - 小物体が滑らない条件は
F≦μN
より
mgsinθ≦μmgcosθ
∴ μ≧tanθ
(これが正解です)
不合格者さんでも正解してくるレベルです。
よって、全ての受験生さんが正解したい問題です。
大問2
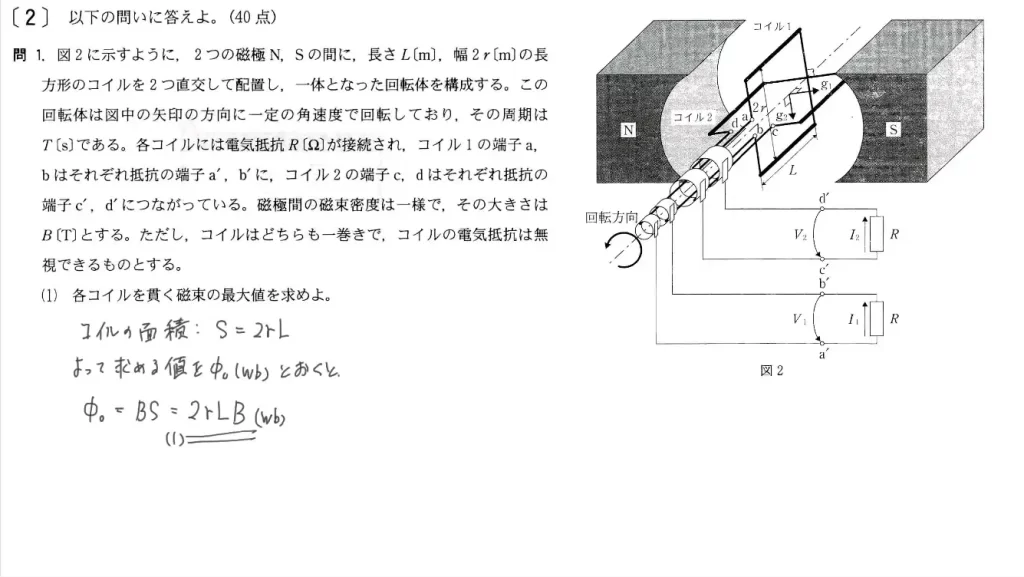
以下「単位」を省略して書きます。
回答の際は単位を付けてください。
問1(1)に関して、各コイルを貫く「磁束の最大値」を答えます。
ポイントは「コイルの角度」です。
コイルが磁束に対して正対する時が「磁束の最大」になる時です。
- コイルの面積をSとおくと
S=2rL - よって、求める磁束の最大値Φ₀は
Φ₀=BS=2rLB…①
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(2)(ア)に関して、コイル2を貫く磁束の「時間変化を表すグラフ」を答えます。
- コイルの角速度をωとおくと
図4(a)で表されるΦ₁は
Φ₁=Φ₀cosωt…②
となる - 題意より
g₂はg₁よりπ/2だけ遅れて回転しているので
Φ₂=Φ₀cos(ωt-π/2)
=Φ₀sinωt…③
となる - よって
正解はグラフ(b)
(これが正解です)
上記では立式して正解を出していますが、図3とグラフ(a)から直感的に正解を選ぶことは難しくありません。
よって、不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問1(2)(イ)(ウ)に関して、コイル1・2に生じる「起電力の時間変化を表すグラフ」を答えます。
ポイントは「電磁誘導の法則」です。
「磁束の変化」を妨げる向きに、誘導起電力が発生します。
- 電磁誘導の法則と①より
V₁=-dΦ₁/dt
=ωΦ₀sinωt - よってV₁のグラフは(b)
(これが正解です) - 電磁誘導の法則と②より
V₂=-dΦ₂/dt
=-ωΦ₀cosωt - よってV₂のグラフは(c)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問1(3)に関して、コイルに流れる誘導電流が磁場から受ける力の最大値をFとした時、コイルの回転周期をn倍にした場合に受ける「力の最大値F’」を答えます。
ポイントは「式変形」です。
コイルの一辺が受ける力は「IBL」ですが、これをそのまま回答にはできません。回答に使える文字になるまで式変形していきましょう。「Fとn」を用いて書き表せとの事なので、まずはFを出す必要がありそうです。
- コイル1を使って考える
- コイル1の辺が受ける力をf₁とおくと
f₁=I₁BL
=V₁BL/R
=ωΦ₀sinωt・BL/R
=2π/T・2rBL・sin2πt/T・BL/R(∵①)
=4πB²L²r/TR・sin2πt/T - よって
Maxf₁=F=4πB²L²r/TR - ここで回転体の周期をn倍にすると
F’=4πB²L²r/nTR
=F/n
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(1)に関して、ここでシチュエーションが変わります。金属板Mが挿入された平行板コンデンサーに関して、コンデンサーの下側の極板と金属Mの間の「静電容量C₁」を答えます。
- C₁=ε₀S/d…③
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(2)に関して、平行板コンデンサーの「静電容量C」を答えます。
ポイントは「直列つなぎ」です。
平行板コンデンサーが金属板Mで分断された2ヶ所は、2つのコンデンサーの直列つなぎとみなすことができます。よって「合成容量」に持ち込めば良いとわかります。
- 問2(1)と同様にして
上側の極板と金属板Mの間の
静電容量C₂は
C₂=ε₀S/2d…④ - 求める値は③と④の合成容量なので
1/C=1/C₁+1/C₂
∴ C=ε₀S/3d…⑤
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(3)に関して、金属板Mの上面に帯電している「電気量QM」を答えます。
ポイントは「コンデンサーの上側の極板」です。
問2(2)でコンデンサーの静電容量を求めたので、電源電圧と合わせて「帯電した電気量」が求まります。金属板Mの上面は、コンデンサーの上側極板と静電容量C₂のコンデンサーを形成しているとみなせるため、帯電した電気量は平行板コンデンサーに等しくなります。
- コンデンサーの極板に
帯電している電気量をQ₀とおくと
⑤より
Q₀=CV=ε₀SV/3d…⑥ - コンデンサーの上側の極板は
+Q₀に帯電しているので
向かい合わせの金属板Mの上面は
QM=-Q₀
=-ε₀SV/3d
=-1/3・C₁V
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問2(4)に関して、平行板コンデンサーの「位置ごとの電界の強さ」をグラフに描きます。
- 金属板Mの下側と
コンデンサーの下側極板の電位差をV₁とおくと
Q₀=V₁C₁
∴ V₁=Q₀/C₁
=1/3・V(∵③⑥) - 金属板Mの上側と
コンデンサーの上側極板の電位差をV₂とおくと
Q₀=V₂C₂
∴ V₂=Q₀/C₂
=2/3・V(∵④⑥) - 金属板の上側の電場の強さをE₂
下側をE₁とおくと
E₂=2/3・V/2d
=V/3d
E₁=1/3・V/d
=V/3d - よって、正解は以下の図となる

不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(5)に関して、コンデンサーの上側極板を距離dだけ金属板Mに近づけた時の「静電エネルギーがどれだけ増えたか」を答えます。
- 上側極板を移動させたことにより
上側極板と金属板Mの間の静電容量C₂’は
C₂’=ε₀S/d
となる - よって
コンデンサーの合成容量C’は
1/C’=1/C₁+1/C₂’
∴ C’=ε₀S/2d=1/2・C₁…⑦
となる - よって、極板の移動前後の
コンデンサーの静電エネルギーを
UおよびU’とおくと
U=1/2・CV²
=1/2・C₁/3・V²(∵③⑤)
=1/6・C₁V²
U’=1/2・C’V²
=1/2・C₁/2・V²(∵⑦) - よって、求める増加量ΔUは
ΔU=U’-U
=1/12・C₁V²
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
大問3
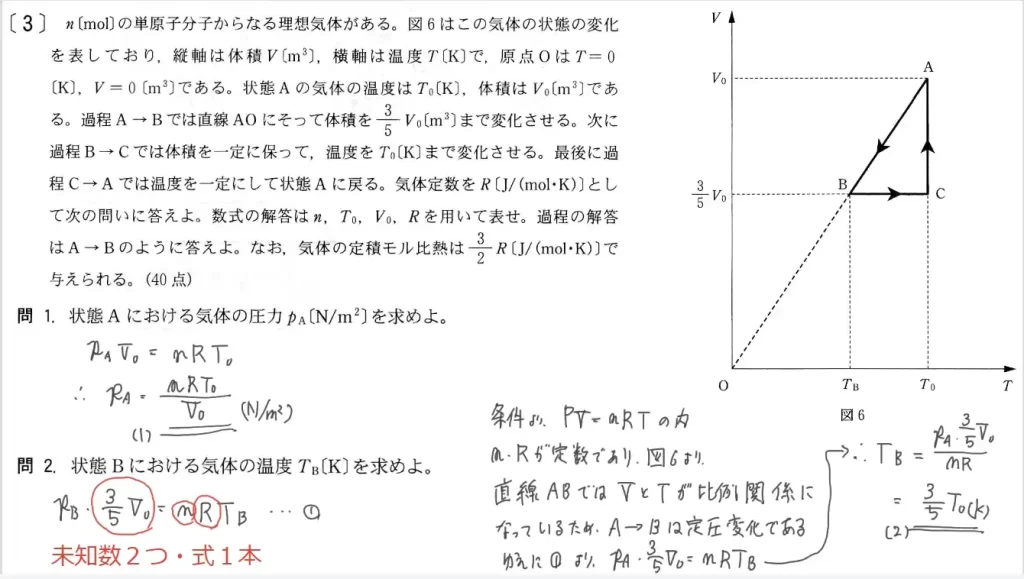
以下「単位」を省略して書きます。
回答の際は単位を付けてください。
問1に関して、状態Aにおける「気体の圧力pA」を答えます。
ポイントは「状態方程式」です。
- 状態方程式より
pA・V₀=nRT₀
∴ pA=nRT₀/V₀…①
(これが正解です)
不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問2に関して、状態Bにおける「気体の温度TB」を答えます。
ポイントは「図6・VTグラフの比例関係」です。
A→Bの直線が原点を通っているため、VとTは比例関係になっています。よって、変化A→Bは「定圧変化」と読み取れます。
- 題意より
nとRは定数であり
図6の変化A→Bにおいて
VとTが比例関係になっているため
変化A→Bは定圧変化である - よって、Bにおける状態方程式より
pA・3/5・V₀=nRTB…②
となる - ①②より
TB=3/5・T₀
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問3に関して、状態Cにおける「気体の圧力pC」を答えます。
- 状態Cにおける状態方程式より
pC・3/5・V₀=nRT₀
∴ pC=5nRT₀/3V₀
(これが正解です)
不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問4に関して、気体の内部エネルギー変化が「正である過程」を答えます。また、その「変化量ΔU」を答えます。
ポイントは「温度が上昇する変化」です。
気体の内部エネルギー変化は温度によって決まります。
- 温度変化をΔTとおくと
題意より
ΔU=3/2・nRΔT - よって、内部エネルギー変化が正となるのは
温度が上昇する変化であり
B→Cとなる
(これが正解です) - また、変化量は
ΔU=3/2・nR(T₀-3/5・T₀)
=3/5・nRT₀
(これが正解です)
不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問5に関して、気体の「内部エネルギー変化が0になる過程」を答えます。
- 問4と同様にして
ΔT=0となる時は
C→Aの過程である
(これが正解です)
問4と同様です。
全ての受験生さんが正解したい問題です。
問6に関して、気体が「外部から仕事をされる過程」を答えます。
ポイントは「気体の体積が減少する変化」です。
気体が外部へ仕事をする時、気体の体積は増加します。今回は「仕事をされる」なので、体積が減少する変化を考えます。
- 気体が外部から仕事をされるのは
体積が減少する時なので
図6より
A→Bの過程である
(これが正解です) - また、この定圧変化で気体がされる仕事Wは
-W=pA(3/5・V₀-V₀)…③ - ①③より
W=2/5・nRT₀
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問7に関して、気体が「外部に熱を放出する過程」を答えます。また、その「熱量Q」を答えます。
ポイントは「熱力学第一法則」です。
「温度が下がり」かつ「体積も減る」変化があれば、その時点で「熱が放出される」とわかります。実はその様な変化が図6にあります(A→B)
- 熱力学第一法則より
温度が下がり、かつ体積も減る
A→Bの過程で
外部に熱が放出されるとわかる
(これが正解です) - この過程における
内部エネルギーの変化ΔUは
ΔU=3/2・nR(TB-T₀)
=-3/5・nRT…④(∵問2) - 気体が外部からされる仕事は
問6で求めているので
③④と熱力学第一法則より
-Q=ΔU+(-W)
∴ Q=-ΔU+W
=nRT₀
(これが正解です)
不合格者さんには難しく、合格者さんは正解してくる問題です。
よって、合否を分ける1問です。
問8に関して、C→Aの過程の代わりに状態Cから断熱的に変化させて状態Aと同じ圧力にした時(この状態をDとする)状態Dの体積VDを「正しく表した選択肢」を5択から答えます。
ポイントは「pVグラフ」です。
与えられた図6は「VTグラフ」ですが、これを「pVグラフ」に描きなおすと正解が見えやすくなります。
- 定圧モル比熱をCpとおくと
題意より
Cp=Cv+R=5/2・R
となる - また比熱比は
γ=Cp/Cv=5/3
となるので
pV⁵/³=一定…(X)
となる - 今、C→Aは等温変化なので
pV=一定…(Y) - また、C→Bは定積変化なので
pVグラフにおいて
p軸に沿って真っすぐ下がる…(Z) - よって(X)(Y)(Z)より
pVグラフを描くと
3/5・V₀<VD<V₀
となるので選択肢③が該当する
(これが正解です)
合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し難しい問題です。
問9に関して、状態Dにおける「気体の温度TDを正しく表した選択肢」を5択から答えます。
- 問8で描いたpVグラフより
TB<TD<T₀
となるので選択肢③が該当する
(これが正解です)
問8が正解できればセットで正解できます。
よって、問8とセットで、合否を分ける1問より少し難しい問題です。
九州大学の物理2005年・平成17年度
大問1
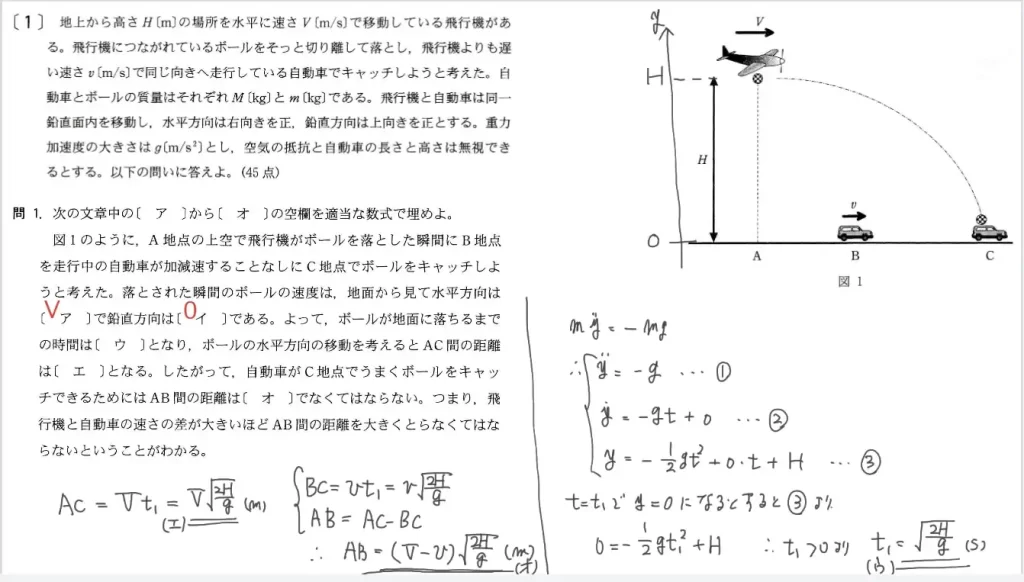
以下「単位」を省略して書きます。
回答の際は単位を付けてください。
問1(ア)~(ウ)に関して、飛行機から落とされたボールが「地面に落ちるまでの時間」を答えます。
ポイントは「自由落下」です。
飛行機から落とされたボールにかかる力は「重力」のみとなります。
- 落とされた瞬間のボールの速度は
水平方向は「ア:V」
鉛直方向は「イ:0」 - ボールの鉛直方向の運動は
自由落下なので
等加速度直線運動の式より
H=1/2・gt²
∴ t=√(2H/g)…①
(これがウの正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(エ)に関して、図1における「ACの距離」を答えます。
ポイントは「等速直線運動」です。
ボールは水平方向に一定速度Vで運動します。
- ボールは水平方向に速度Vで運動するので
①より
AC=Vt=V√(2H/g)…②
(これが正解です)
不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問1(オ)に関して、図1における「ABの距離」を答えます。
ポイントは「飛行機と自動車の移動距離」です。
ABの長さは「飛行機の移動距離-自動車の移動距離」と言い換えることができます。
- ①より
BC=vt=v√(2H/g)…② - ①②より
AB=AC-BC
=(V-v)√(2H/g)
(これが正解です)
不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問2(1)に関して、C地点で地面と衝突する直前の「ボールの鉛直方向の速度」を答えます。
- 求める速度をUとおくと
鉛直上向きを正として①より
U=-gt=-√(2gH)…③
(これが正解です)
問2になりましたが、まだ基本問題が続いてます。
全ての受験生さんが正解したい問題です。
問2(2)に関して、ボールが1回目・2回目に落ちてくる地点「C・D間の距離」を答えます。
ポイントは「はね返りの式」です。
はね返りの式を書くと、地面に衝突直後のボールの鉛直方向速度が求まります。あとは「投げ上げ運動」という流れです。
- 反発係数をe
ボールが地面と衝突した直後の
鉛直方向速度をU’とおくと
はね返りの式と③より
U’-0=-e(U-0)
∴ U’=-eU
=√(gH/2)…④ - C地点で跳ね返ってから
D地点に落ちるまでの時間を
t’とおくと
0=U’t’-1/2・gt’²
∴ t’=2U’/g
=√(2H/g)…⑤(∵④) - よって
CD=Vt’=V√(2H/g)(∵⑤)
(これが正解です)
「バウンド中の時間」と「はね返りの式」が出て難易度が上がりました。
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(3)に関して、AD間での「自動車の加速度」を答えます。
ポイントは「求める加速度をaとおくこと」です。
自動車は等加速度直線運動であり、その「時間」と「距離」は以下のように判明しています。
| ACの長さ | 問1(エ) |
| CDの長さ | 問2(2) |
| ボールが1回目に 落ちるまでの時間 | 問1(ウ) |
| ボールの最初の バウンド時間 | 問2(2) |
よって、加速度をaとおいて立式すれば「未知数1つ・式1本」で正解となります。
- 自動車が移動する時間をTとおくと
それはボールがDに到達するまでなので
T=t+t’
=2√(2H/g)…⑥ - AD=AC+CD
=2V√(2H/g)…⑦ - 求める自動車の加速度をaとおくと
自動車は等加速度直線運動するので
AD=vT+1/2・aT²
∴ a=(V-v)√(g/2H)(∵⑥⑦)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(4)に関して、自動車の出せる最大の速さをvMとした時、D地点で自動車がボールに追いつくための「飛行機の速さVが満たすべき条件」を答えます。
ポイントは、問題文「AD間での自動車の加速度は一定」です。
この問題は一見すると
- AD間のどこかで速さvMに達した自動車が
- そこから加速を止めて速さvMで走り続ける
状況を考えたくなりますが、問題文の通り「自動車は一定加速度で加速し続け」ます。つまり「D地点で速さvMを超えなければよい」というだけの問題です。
- D地点における
自動車の速さをvDとおくと
vD=v+aT
=2V-v - 自動車の最大の速さがvMなので
vM≧2V-v
∴ V≦(vM+v)/2
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問2(5)に関して、D地点でボールをキャッチした直後の「自動車の速度」を答えます。
ポイントは「運動量保存則」です。
問題文に「ボールをキャッチする直前に加速をやめた」と書いてあるので「運動量保存を使う」とわかります。
- 求める自動車の速度をuとおくと
水平方向の運動量保存則より
(m+M)u=mV+M(2V-v)
∴ u={mV+M(2V-v)}/(m+M)
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
大問2

以下「単位」を省略して書きます。
回答の際は単位を付けてください。
問1(ア)に関して、導線の長さLの部分が受ける「力の大きさF」を答えます。
- F=IBLsinθ
不合格者さんでも正解してきます。
全ての受験生さんが正解したい問題です。
問1(イ)~(エ)に関して、接続点bにおける「電流の関係」および閉回路abcdefにおける「電圧の関係」を答えます。
ポイントは「キルヒホッフの法則」です。
【キルヒホッフの第一法則】
流れ込む電流の和は、流れ出す電流の和に等しい
【キルヒホッフの第二法則】
任意の閉回路で電位差の和は0となる
- (イ)の法則名は
「イ:キルヒホッフ」 - b点に流れ込む電流は
I₁+I₂+I₃
b点から流れ出す電流は
0 - よってキルヒホッフの第一法則より
I₁+I₂+I₃=0
∴ I₁=-I₂-I₃
(これが正解です) - 閉回路abcdefに関して
キルヒホッフの第二法則より
E₁-I₁R₁-(-I₃)R₃-E₃=0
∴ E₁=I₁R₁-I₃R₃+E₃
(これが正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(1)に関して、時刻t=0~5までに図4の閉回路に生じる「誘導起電力をグラフで」答えます。
ポイントは「電磁誘導の法則」です
【電磁誘導の法則】
V=|ΔΦ/Δt|(V)
- 図5の磁束の変化より
- 0≦t≦1の時
V=|2/1|=2…①
向きは正方向 - 1≦t≦3の時
V=0…② - 3≦t≦5の時
V=|-2/2|=1…③
向きは負方向
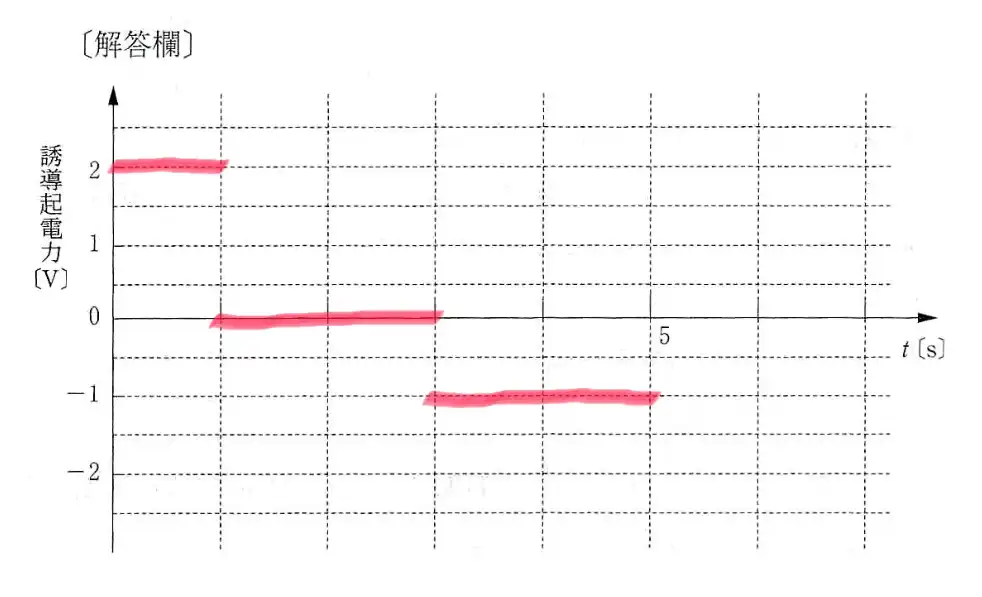
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2(2)に関して、t=0~5の間に回路全体から発生する「ジュール熱」を答えます。
- ジュール熱をW
回路全体の抵抗をRとおくと
W=V²t/R…④ - ④と①~③より
0≦t≦1の時
W=2/3
1≦t≦3の時
W=0
3≦t≦5の時
W=1/3 - よって
求めるジュール熱の総量は
1(J)
(これが正解です)
不合格者さんでも正解してくるレベルです。
しかし、本問に参加するには問2(1)の正解が必要です。
よって、問2(1)とセットで、合否を分ける1問より少し簡単な問題です。
問3(1)に関して、時刻「L/v<t<2L/v」において「辺afに流れる電流I₁」および「辺cdに流れる電流I₂」を答えます。
ポイントは「キルヒホッフの法則」です。
本問が解きやすくなるように、問1で「キルヒホッフの法則」の基本問題が出されています。活用しましょう。
- 図6において
e→bの向きに流れる電流をI₃とおく - 回路が磁場内を移動して
生じる誘導起電力は
vBL - 点eに関して
キルヒホッフの第一法則より
I₁+I₂=I₃…⑤ - 回路bcdebに関して
キルヒホッフの第二法則より
vBL-I₃R-I₂R=0…⑥ - 回路abcdefaに関して
キルヒホッフの第二法則より
vBL-(-I₁)R-I₂R=0…⑦ - よって⑤⑥⑦より
I₁=-vBL/3R
I₂=2vBL/3R
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
問3(2)に関して、時刻「2L/v<t<3L/v」において「辺afに流れる電流I₁」および「辺cdに流れる電流I₂」を答えます。
- 回路が磁場内を移動して
生じる誘導起電力は
c→d方向:vBL
b→e方向:vBL - 点eに関して
キルヒホッフの第一法則より
I₁+I₂=I₃…⑧ - 回路bcdebに関して
キルヒホッフの第二法則より
vBL-vBL-I₃R-I₂R=0…⑨ - 回路abcdefaに関して
キルヒホッフの第二法則より
vBL-(-I₁)R-I₂R=0…(10) - よって⑧⑨(10)より
I₁=-2vBL/3R
I₂=vBL/3R
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
大問3

以下「単位」を省略して書きます。
回答の際は単位を付けてください。
問1(ア)に関して、状態Aの「内部エネルギー」を答えます。
ポイントは「温度TAを自分で設定すること」です。
これにより、状態方程式と内部エネルギーの式を立てやすくなります。
- 状態Aにおける気体の温度をTAとおくと
状態方程式より
P・SL=1・R・TA
∴ PSL=RTA…① - また、題意より
内部エネルギーUAは
UA=3/2・RTA…② - よって①②より
UA=3/2・PSL…③
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(イ)に関して、状態A→Bの過程における「気体に加えた熱量Q₁」を答えます。
ポイントは「熱力学第一法則」です。
受け取った熱量=内部エネルギー変化+外部へした仕事
- 状態Bにおける気体の温度をTBとおくと
状態方程式より
2P・SL=1・R・TB
∴ 2PSL=RTB…④ - ①④より
TB=2TA - ゆえに③より
UB=2UA=3PSL…⑤ - よって
③⑤と熱力学第一法則より
Q₁=ΔU+0
=UB-UA
=3/2・PSL…⑥
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(ウ)(エ)に関して、状態B→Cにおける「内部エネルギーの変化」および「気体がした仕事W₁」を答えます。
ポイントは「熱力学第一法則」です。
状態B→Cは定圧変化ではないため「仕事=圧力×体積変化」とは書けませんが、熱力学第一法則を用いれば仕事W₁が求まります。
- 状態Cにおける状態方程式より
P・SLC=1・R・TC
∴ TC=PSLC/R
∴ UC=3/2・PSLC…⑦ - よって⑤⑦より
UC-UB=-3/2・PS(2L-LC)…⑧
(これが正解です) - また、状態B→Cは断熱変化なので
熱力学第一法則より
0=⑧+W₁
∴ W₁=3/2・PS(2L-LC)
(これが正解です)
不合格者さんでも正解してきます。
よって、全ての受験生さんが正解したい問題です。
問1(オ)~(カ)に関して、状態C→Aにおける「内部エネルギー変化」および「気体がした仕事W₂」「気体から奪った熱量Q₂」を答えます。
ポイントは「状態C→Aが定圧変化」であることです。
問題文より、状態AとCでピストンを固定していない事が読み取れます。よって、状態AとCにおける気体の圧力は「外圧に等しい」です。
- ③⑦より
UA-UC=-3/2・PS(LC-L)…⑨
(これがオの正解です) - 状態CおよびAの気体の圧力はPであり
状態C→Aは定圧変化なので
W₂=PΔV
=P(SL-SLC)
=-PS(LC-L)…(10)
(これがカの正解です) - ⑨(10)および
熱力学第一法則より
-Q₂=(UA-UC)+W₂
∴ Q₂=5/2・PS(LC-L)
(これがキの正解です)
不合格者さんの一定数が不正解になるレベルです。
よって、合否を分ける1問より少し簡単な問題です。
問2・問3に関して、気体に加えた熱量Q₁と気体から奪った熱量Q₂の「関係を正しく表した選択肢」を答えます。また、W₁・W₂・Q₁・Q₂の間に「成り立つ関係式」を答えます。
ポイントは「PVグラフ」です。
本問では「気体がした仕事」と「気体がされた仕事」の大小関係から正解を導きますが、その大小関係は細かく計算式を評価するより、PVグラフを描けば視覚的にわかります。
- 状態A→B→C→Aの1サイクルにおいて
温度が初期状態に戻るため
内部エネルギーの変化は0となる - よって
気体の熱量と仕事の関係は
Q₁-Q₂=W₁+W₂…(11)
(これが問3の正解です) - またW₁とW₂の大小関係について
PVグラフを描くと
W₂の領域はW₁の領域の一部となるため
W₁>-W₂
であるとわかるため
W₁+W₂>0…(12)
となる - よって(11)(12)より
Q₁-Q₂>0
∴ Q₁>Q₂
(これが正解です)
不合格者さんには難しく、合格者さんは準備できているレベルです。
よって、合否を分ける1問です。
問4に関して、状態Bから状態Cと同じ圧力になるまで等温膨張させた時(この状態をC*とする)C*におけるシリンダーの底面からピストンまでの距離LC*とLCの「関係を正しく表した選択肢」を3択から答えます。
- 題意より
状態Bから状態C・C*への変化は
以下の表のとおりとなる
| B→C | 断熱変化 | PV^γ=一定 γ>1 |
| B→C* | 等温変化 | PV=一定 |
- よって
状態Cおよび状態C*の圧力を等しくした時
体積は
状態C<状態C*
となる - よって
LC<LC*
(これが正解です)
不合格者さんには難しく、合格者さんは乗り越えてくるレベルです。
よって、合否を分ける1問です。
おわりに
上記の考え方で取り組んでいけば、高校偏差値60の高校で落ちこぼれて
- 1番簡単な国立大学を目指せない
- 九州工業大学・熊本大学など想像できない
という学生さんでも、トップ高校との「才能の差」を補って九大合格できます。
「九大物理の攻略法」は現在執筆中です。
考え方は「数学・英語」と同じなので、よかったら以下を御覧ください。




